中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 第1章 插值 概念 实际中,)多样,复杂,通常只能观测到一些离散数据; 或者fx)过于复杂而难以运算。这时我们要用近似函数g:来 逼近fxy)。 自然地,希望9c)通过所有的离散点 g)≈x) X2 X3
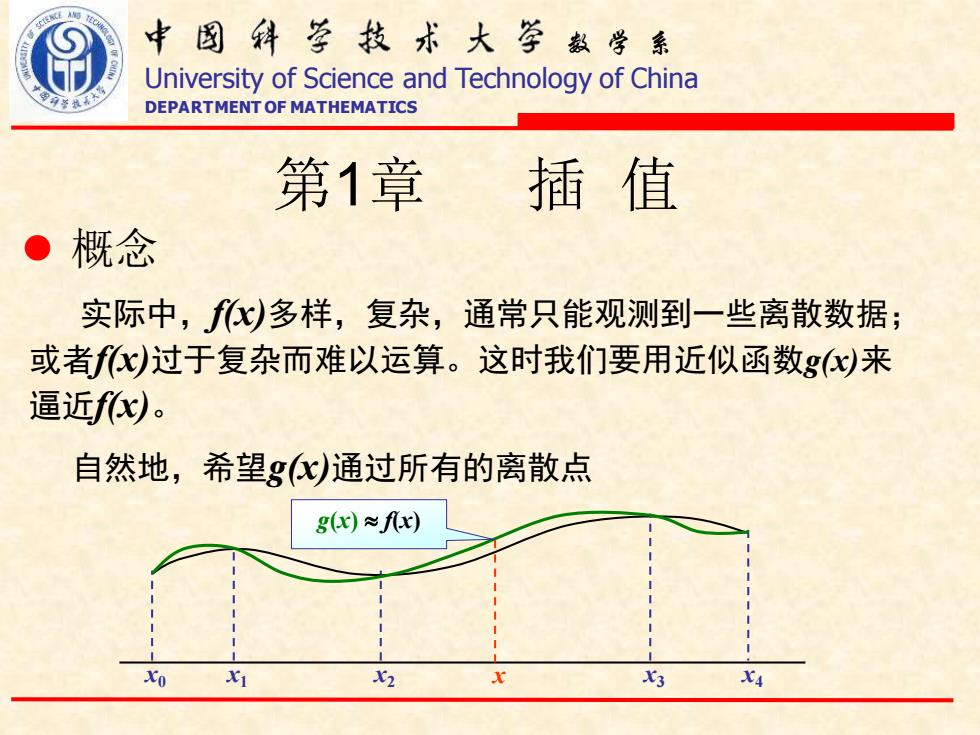
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 第1章 插 值 实际中,f(x)多样,复杂,通常只能观测到一些离散数据; 或者f(x)过于复杂而难以运算。这时我们要用近似函数g(x)来 逼近f(x)。 自然地,希望g(x)通过所有的离散点 ⚫ 概念 x0 x1 x2 x x3 x4 g(x) f(x)

中图 品剂 科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 定义:fd为定义在区间【a,]上的函数,{x}”为区间上n+1个互不 相同的点,Φ为给定的某一函数类。求Φ上的函数g(x)满足 g(x)=f(x),i=0,.,n 问题 ·是否存在唯一 ·如何构造 ·误差估计
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 定义: 为定义在区间 上的函数, 为区间上n+1个互不 相同的点, 为给定的某一函数类。求 上的函数 满足 f (x) a,b 0 n i i x = g(x) g(xi ) = f (xi ) , i = 0, ,n 问题 ⚫ 是否存在唯一 ⚫ 如何构造 ⚫ 误差估计

中图科萝技术大空数学案 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 设g(x)=aop(x)+·+a,pn(x) 则 g(x,)=f(x;)=dopo(x)+.+an (x;) aopo(xo)+a(xo)+.+a,(xo)=f(xo) aopo()+ae(x)+.+a,e (x)=f(x) aopo(x)+ae(x)+.+a,(x)=f(x) 所以{=有解,当且仅当系数行列式不为0
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 0 0 0 0 ( ) ( ) ( ) ( ) ( ) ( ) ( ) n n i i i n n i g x a x a x g x f x a x a x = + + = = + + 设 则 0 0 0 1 1 0 0 0 0 0 1 1 1 1 1 1 0 0 1 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) n n n n n n n n n n a x a x a x f x a x a x a x f x a x a x a x f x + + + = + + + = + + + = 所以 { } 0 有解,当且仅当系数行列式不为0 n i i a =

中图科萝技术大学数学桑 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 存在唯一定理 定理1.1{x}0为n+1个节点,Φ=pan{po,p1,.pn} n+1维空间,则插值函数存在唯一,当且仅当 p(x).p(xo) ≠0 9(xn).p(xn
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 存在唯一定理 定理1.1 : 为n+1个节点, n+1维空间,则插值函数存在唯一,当且仅当 0 n i i x = = span{0 ,1 , n } 0 ( ) ( ) ( ) ( ) 0 0 0 0 n n n n x x x x

中图斜亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 特点: 1.与基函数无关 2.与原函数fx无关 3.基函数个数与点个数相同
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 1. 与基函数无关 2. 与原函数f(x)无关 3. 基函数个数与点个数相同 特点:

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 对应于D=P"(x)=Span{L,x,x2,.x"} 则 = Πs-x≠0 x 0≤j<isn Vandermonde行列式
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS ( ) {1, , , } n 2 n 对应于 = x = span x x x 则 0 1 1 0 0 = − jin i j n n n x x x x Vandermonde行列式

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 多项式插值的Lagrange型 ●如何找? 在基函数上下功夫,取基函数为{L,(x)}”。P” 求)-成0i/则w-空(rx
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 多项式插值的Lagrange型 ⚫ 如何找? 在基函数上下功夫,取基函数为 n n i x i {l ( )} =0 要求 = = = i j i j l i xj i j 1, 0, ( ) 则 ( ) ( ) ( ) 0 i n i i g x l x f x = =

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 求{L,(x)}”o,易知: L,(x)=a,(x-xo)(x-x,-1)(x-x+1)(x-xn) a, 1 (x,-xo)(x,-x,-1)(x-x+1)(x,-xn) (x-xo).(x-x,-1)(x-x+1)(x-xn) =-).(x-x4x-(x) i记o,(0)-Π(x-)+1,()=D,(xx-x) ⊙n(x)
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 求 n i x i l 0 { ( )} = ,易知: ( ) ( ) ( )( ) ( ) i x ai x x0 x xi 1 x xi 1 x xn l = − − − − + − ( ) ( )( ) ( ) 1 i 0 i i 1 i i 1 i n i x x x x x x x x a − − − − = − + 0 1 1 0 1 1 ( ) ( )( ) ( ) ( ) ( )( ) ( ) i i n i i i i i i i n x x x x x x x x l x x x x x x x x − + − + − − − − = − − − − 0 ( ) ( ) n n i i x x x = 记 = − ( ) ( ) ' ( )( ) n i n i i x l x x x x = −

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS ·线性插值 ()=x- ,1(x)=x- X0-X1 X1-X0 L (x)=f(o)(x)+f(x(x)
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS ⚫线性插值 1 0 0 1 0 1 1 0 ( ) , ( ) x x x x l x x x x x l x − − = − − = ( ) ( ) ( ) ( ) ( ) 1 0 0 1 1 L x = f x l x + f x l x

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS ·二次插值 h(x)=x-x-x) 4(x)=x-x-x) (x-x)-x2) (x1-x0)x1-x2) (x)= (x-x)(x-x) x2-)(x2-x) L(x)=f(xo)(x)+f(x(x)+f(x(x)
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS ⚫二次插值 1 2 0 0 1 0 2 ( )( ) ( ) ( )( ) x x x x l x x x x x − − = − − 2 0 0 1 1 2 2 L x f x l x f x l x f x l x ( ) ( ) ( ) ( ) ( ) ( ) ( ) = + + 0 2 1 1 0 1 2 ( )( ) ( ) ( )( ) x x x x l x x x x x − − = − − 0 1 2 2 0 2 1 ( )( ) ( ) ( )( ) x x x x l x x x x x − − = − −