
中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 第8章 常微分方程 实际中,很多问题的数学模型都是微分方程。我们 可以研究它们的一些性质。但是,只有极少数特殊的方程 有解析解。对于绝大部分的微分方程是没有解析解的。 常微分方程作为微分方程的基本类型之一,在自然界 与工程界有很广泛的应用。很多问题的数学表述都可以归 结为常微分方程的定解问题。很多偏微分方程问题,也可 以化为常微分方程问题来近似求解。 本章讨论常微分方程的数值解法
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 第8章 常微分方程 实际中,很多问题的数学模型都是微分方程。我们 可以研究它们的一些性质。但是,只有极少数特殊的方程 有解析解。对于绝大部分的微分方程是没有解析解的。 常微分方程作为微分方程的基本类型之一,在自然界 与工程界有很广泛的应用。很多问题的数学表述都可以归 结为常微分方程的定解问题。很多偏微分方程问题,也可 以化为常微分方程问题来近似求解。 本章讨论常微分方程的数值解法

中图科学技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 对于一个常微分方程: y= =f(x.y)xela.b dx 通常会有无穷个解。如: =cos(N)→y=sm(x)+a,Va∈R dx 因此,我们要加入一个限定条件。通常会在端点出给出,如下面 的初值问题: (xela dx y(a)=yo 为了使解存在唯一,一般,要加限制条件在∫上,要求对满足 Lipschit讴条件: f(x,)-f(x,2≤L4-2
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 对于一个常微分方程: ' f (x, y) , x [a,b] dx dy y = = 通常会有无穷个解。如: x y x a a R dx dy = cos( ) = sin( ) + , 因此,我们要加入一个限定条件。通常会在端点出给出,如下面 的初值问题: = = 0 ( ) ( , ) , [ , ] y a y f x y x a b dx dy 为了使解存在唯一,一般,要加限制条件在f上,要求f对y满足 Lipschitz条件: 1 2 1 2 f (x, y ) − f (x, y ) L y − y

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 常微分方程的解是一个函数,但是,计算机没有办法对函数 进行运算。因此,常微分方程的数值解并不是求函数的近似,而 是求解函数在某些节点的近似值。 例:我们对区间做等距分割:x=hi,h=(b-a)/m 设解函数在节点的近似为y,},则: dx =f(x,y) x=x 由数值微分公式,我们有 向前差商公式 y-≈f(x,y) h yi=y;+hf(x,y;) 可以看到,给出初值,就可以用上式求出所有的{}
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 常微分方程的解是一个函数,但是,计算机没有办法对函数 进行运算。因此,常微分方程的数值解并不是求函数的近似,而 是求解函数在某些节点的近似值。 例:我们对区间做等距分割: , ( ) / i x h i h b a m = = − 设解函数在节点的近似为 { }i y 由数值微分公式,我们有 i i x x x x f x y dx dy = = = ( , ) ,则: ( , ) 1 i i i i f x y h y y + − 向前差商公式 ( , ) i 1 i i i y = y + h f x y + 可以看到,给出初值,就可以用上式求出所有的{ }i y

中图斜亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 这种方法,称为数值离散方法。求的是在一系列离散点列上, 求未知函数y在这些点上的值的近似。 基本步骤如下: ①对区间作分割:△:a=x<x,<<xn=b 求yx在x;上的近似值y。{y,}称为分割△,上的格点函数 我们的目的,就是求这个格点函数 ②由微分方程出发,建立求格点函数的差分方程。这个方程满足: A、解存在唯一;B、稳定,收敛;C、相容 ③解差分方程,求出格点函数 数值方法,主要研究步骤②,即如何建立差分方程,并研究差分 方程的性质
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 基本步骤如下: ③ 解差分方程,求出格点函数 ① 对区间作分割: I : a = x0 x1 xn = b 求y(x)在xi上的近似值yi。 { }i y 称为分割 I 上的格点函数 ② 由微分方程出发,建立求格点函数的差分方程。这个方程满足: A、解存在唯一;B、稳定,收敛;C、相容 数值方法,主要研究步骤②,即如何建立差分方程,并研究差分 方程的性质。 这种方法 ,称为数值离散方法。求的是在一系列离散点列上, 求未知函数y在这些点上的值的近似。 我们的目的,就是求这个格点函数

中图科李技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 为了考察数值方法提供的数值解,是否有实用价值,需要知 道如下几个结论: ①收敛性问题 步长充分小时,所得到的数值解能否逼近问题的真解; ② 误差估计 ③ 稳定性问题 舍入误差,在以后各步的计算中,是否会无限制扩大;
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 为了考察数值方法提供的数值解,是否有实用价值,需要知 道如下几个结论: ① 收敛性问题 ② 误差估计 ③ 稳定性问题 步长充分小时,所得到的数值解能否逼近问题的真解; 舍入误差,在以后各步的计算中,是否会无限制扩大;
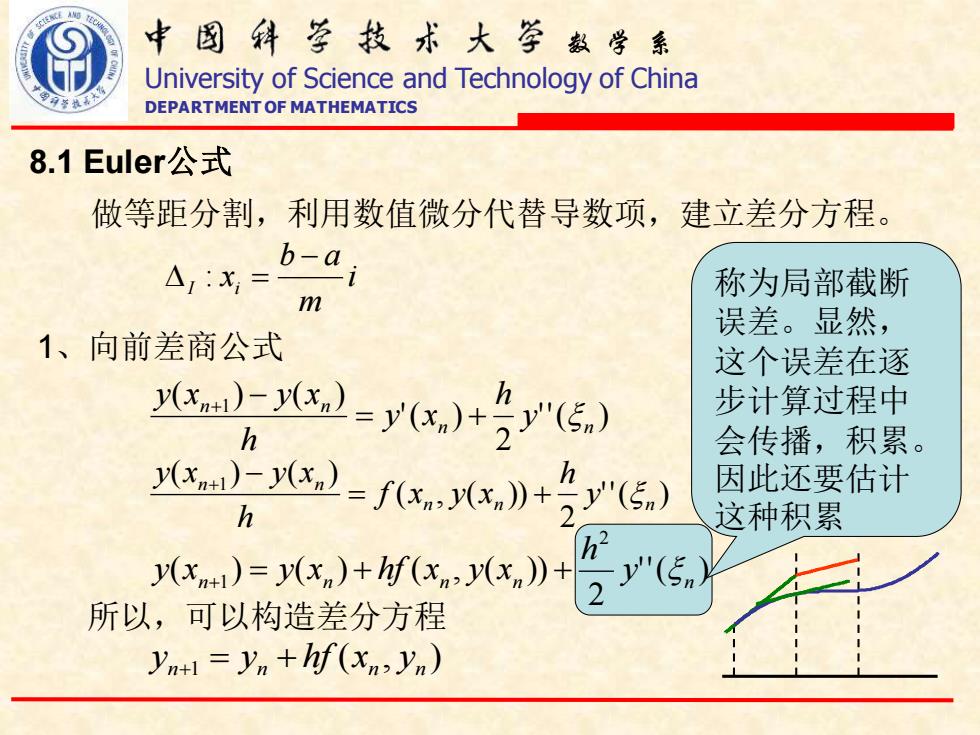
中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 8.1 Euler公式 做等距分割,利用数值微分代替导数项,建立差分方程。 b-ai 称为局部截断 m 误差。显然, 1、向前差商公式 这个误差在逐 -y)+y() 步计算过程中 h 会传播,积累。 区)=fxx》+2"(5.) 因此还要估计 h 这种积累 y(x)=y(x)+hf(xn2 y(x))+ 2(5 所以,可以构造差分方程 ynti=yn+hf(xn2 yn)
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 8.1 Euler公式 做等距分割,利用数值微分代替导数项,建立差分方程。 i m b a x I i − : = 1、向前差商公式 ''( ) 2 '( ) ( ) ( ) 1 n n n n y h y x h y x y x = + + − ''( ) 2 ( , ( )) ( ) ( ) 1 n n n n n y h f x y x h y x y x = + + − ''( ) 2 ( ) ( ) ( , ( )) 2 n 1 n n n n y h y x + = y x + hf x y x + 所以,可以构造差分方程 ( , ) n 1 n n n y = y + hf x y + 称为局部截断 误差。显然, 这个误差在逐 步计算过程中 会传播,积累。 因此还要估计 这种积累

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 定义在假设,=yx),即第i步计算是精确的前提下,考虑 的截断误差R;=y化#)-y+1称为局部截断误差*local truncation error*l。 定义若某算法的局部截断误差为O(+),则称该算法有p阶 精度。 2、收敛性 考察局部误差的传播和积累 y(x)=y(x)+hf(x2 y(x))+ 2y"(5) ynti =yn+hf(xn2yn) 记为hTm+
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 定义 在假设 yi = y(xi ),即第 i 步计算是精确的前提下,考虑 的截断误差 Ri = y(xi+1 ) − yi+1 称为局部截断误差 /* local truncation error */。 定义 若某算法的局部截断误差为O(h p+1 ),则称该算法有p 阶 精度。 记为 2、收敛性 ''( ) 2 ( ) ( ) ( , ( )) 2 n 1 n n n n y h y x + = y x + hf x y x + ( , ) n 1 n n n y = y + hf x y + hTn+1 考察局部误差的传播和积累

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS e=y(x)-y ≤y(xn)-ynl+hf(xn,(xn》-f(xa,yn+hATl ≤en+hLy(xn)-yn+hTl ≤(1+hL)len+hT,T=maxT, ≤1+h)1+hL)en+hT)+h7 =(1+hL)2en+(1+hL)+1)hT ≤(1+hL)2《1+hL)len-2+hT)+(+hL)+1h7 =(1+hL)em-2+(1+hL)2+(1+hL)+1h7 ≤
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 1 1 1 ( ) n+ = n+ − n+ e y x y 1 ( ) ( , ( )) ( , ) n − n + n n − n n + hTn+ y x y h f x y x f x y 1 ( ) n + n − n + hTn+ e hL y x y j j (1+ hL) en + hT , T = max T (1+ hL)((1+ hL) en−1 + hT)+ hT (1 hL) en 1 ((1 hL) 1)hT 2 = + − + + + (1 hL) ((1 hL) en 2 hT) ((1 hL) 1)hT 2 + + − + + + + (1 hL) en ((1 hL) (1 hL) 1)hT 2 2 3 = + − + + + + +
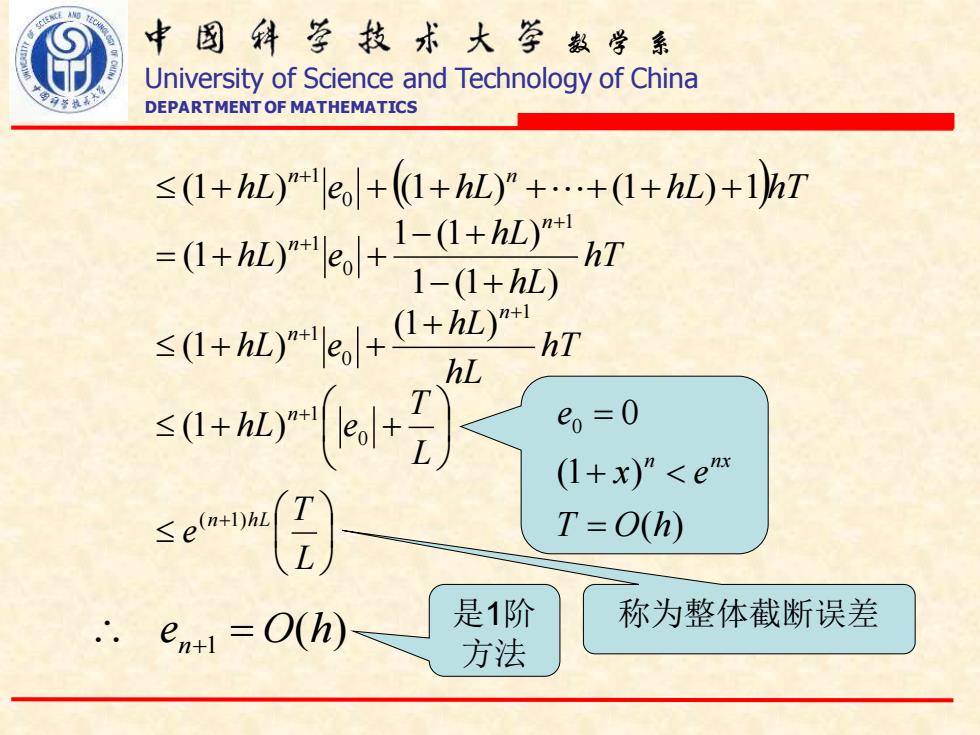
中图科学技术大空数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS ≤(I+hL)mel+(1+hL)”++(1+hL)+1hT =0+rs,+二0+"A 1-(1+hL) s1+L+0+)h7 sd-m) e=0 (1+x)”<em T=O(h) e+1=O(h) 是1阶 称为整体截断误差 方法
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS hL e ( hL hL )hT n n (1 ) 0 (1 ) (1 ) 1 1 + + + + + + + + hT hL hL hL e n n 1 (1 ) 1 (1 ) (1 ) 1 0 1 − + − + = + + + + hT hL hL hL e n n 1 0 1 (1 ) (1 ) + + + + + + + + L T hL e n 0 1 (1 ) + L T e (n 1)hL ( ) en+1 = O h ( ) (1 ) 0 0 T O h x e e n nx = + = 是1阶 称为整体截断误差 方法

中固斜亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 3、稳定性一误差在以后各步的计算中不会无限制扩大。 我们考虑简单情况:仅初值有误差,而其他计算步骤无误差。 设{z,}是初值有误差后的计算值,则 yn+=yn+hf(xn2yn) Ent1=2n+hf(Xn 2n) 所以,我们有: e+i=yn+1-2n+i≤len+hAf(xn,yn)-f(xn,zn)》 e,+hly,-z,=en(1+hL) ≤.≤lell+hL)m1≤eem+hl 可以看出,向前差商公式关于初值是稳定的。当初始误差 充分小,以后各步的误差也充分小
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 3、稳定性-误差在以后各步的计算中不会无限制扩大。 我们考虑简单情况:仅初值有误差,而其他计算步骤无误差。 设 { }i z 是初值有误差后的计算值,则 ( , ) ( , ) 1 1 n n n n n n n n z z hf x z y y hf x y = + = + + + 所以,我们有: ( , ) ( , ) n 1 n 1 n 1 n n n n n e y − z e + h f x y − f x z + + + e hL y z e (1 hL) n + n − n = n + n n hL e hL e e ( 1) 0 1 0 (1 ) + + + 可以看出,向前差商公式关于初值是稳定的。当初始误差 充分小,以后各步的误差也充分小