
第四章球面几何和球面三角 球面几何与平面几何相比较,不难看出有如下特点:(1)相对于其球半径而言,很小的 一片球面可以看成是一个平面。(2)球面几何上的一个大圆在平面几何上相当于扮演者一条 直线.(3)球面几何上的一个大圆与平面几何上的一条直线都有反射对称这个性质. 球面三角学是数学的一个分科,主要研究球面上由三个大圆弧相交所构成的球面三角形 的特性、关系式及其解法等问题 在航海上,当球面三角形的三条边与其所在球的半径相比相当小时,则在容许的误差范 围之内,可视作平面三角形来解。球面三角是船舶驾驶专业两门主要专业课(航海学、航海 天文学)的主要数学基础之一,在学习球面三角之前,先要学习球面几何的基本知识. 4.1球面几何 4.1.1球、球面 空间中与定点0等距离r的所有点的轨迹,称为以0为球心,r为半径的球面,包围在 球面中的实体称为球.连接球面上两点且通过球心的线段称为球直径。半径相等的球称为 等球。 地球其局部地貌虽然是丘陵起伏、山川纵横,但是其全局的形状却十分接近于一个球面。 在航海实际应用上可以把球作为它的第一近似体,航海学和天文航海学的主要问题是定 位,即在地球上确定船帕的地理位置,这是航海专业学生必须掌握的最基本的知识。因此, 必须研究球和球面上的基本点、线、圆以及球面三角形的性质等。 4.1.2大圆 显然,任一平面与球面相截的截痕是圆(如图4.1.1示).一个过球心的截面,在球面上 所截得的圆称为大圆。在平面几何上相当于一条直线.大圆上一段圆周称为大圆弧。反之, 一个不过球心的截面,在球面上所截得的圆称为小圆,小圆上一段圆周称为小圆孤。任何两 个大圆都交于对顶的两点(如图4.1.2示),所以大圆分球和球面为相等的两个部分:且过对 顶的两点能作无数个大圆,而不能作小圆:但如果不过对顶的两点只能作一个大圆,却能作 无数个小圆:两个大圆平面的交线是球的直径也是这两个大圆的直径,并且把两个大圆互相 平分
76 第四章 球面几何和球面三角 球面几何与平面几何相比较,不难看出有如下特点:(1)相对于其球半径而言,很小的 一片球面可以看成是一个平面.(2)球面几何上的一个大圆在平面几何上相当于扮演着一条 直线.(3)球面几何上的一个大圆与平面几何上的一条直线都有反射对称这个性质. 球面三角学是数学的一个分科,主要研究球面上由三个大圆弧相交所构成的球面三角形 的特性、关系式及其解法等问题. 在航海上,当球面三角形的三条边与其所在球的半径相比相当小时,则在容许的误差范 围之内,可视作平面三角形来解. 球面三角是船舶驾驶专业两门主要专业课(航海学、航海 天文学)的主要数学基础之一. 在学习球面三角之前,先要学习球面几何的基本知识. 4.1 球面几何 4.1.1 球、球面 空间中与定点 0 等距离 r 的所有点的轨迹,称为以 0 为球心, r 为半径的球面,包围在 球面中的实体称为球. 连接球面上两点且通过球心的线段称为球直径. 半径相等的球称为 等球. 地球其局部地貌虽然是丘陵起伏、山川纵横,但是其全局的形状却十分接近于一个球面. 在航海实际应用上可以把球作为它的第一近似体. 航海学和天文航海学的主要问题是定 位,即在地球上确定船舶的地理位置,这是航海专业学生必须掌握的最基本的知识. 因此, 必须研究球和球面上的基本点、线、圆以及球面三角形的性质等. 4.1.2 大圆 显然,任一平面与球面相截的截痕是圆(如图 4.1.1 示). 一个过球心的截面,在球面上 所截得的圆称为大圆. 在平面几何上相当于一条直线. 大圆上一段圆周称为大圆弧. 反之, 一个不过球心的截面,在球面上所截得的圆称为小圆,小圆上一段圆周称为小圆弧. 任何两 个大圆都交于对顶的两点(如图 4.1.2 示),所以大圆分球和球面为相等的两个部分;且过对 顶的两点能作无数个大圆,而不能作小圆;但如果不过对顶的两点只能作一个大圆,却能作 无数个小圆;两个大圆平面的交线是球的直径也是这两个大圆的直径,并且把两个大圆互相 平分

图4.1.1 图4.1.2 4.1.3球面距离 球面上一个大圆的长是360°,球面上两点A、B间小于180°的大圆弧(也称劣弧)长 称为球面距离,它是点A、B间的最短球面距离,在航海上称为大圆航线。地球半径大约 为6370km.海上距离的单位是海里,即把地球子午线上'的弧长称为1 nmile.其换算公 式是1nmi1e=1852m 4.1.4轴、极、极距、极线 垂直于任一圆的球直径称为该圆的轴,轴与球面的两个交点称为极,显然,球上任一个 圆都有两个极。从大圆弧或小圆弧上的一点到极的球面距离称为极距。因为同圆上任意一 点的极距都相等,所以也可以称极为该圆的球面中心,称极距为该圆的球面半径 注:球面中心不是圆心:球面半径不是球半径 极距等于90°的大圆弧称为极线或称为赤道.因为任一大圆与其极的极距为90°,所以 大圆弧是它的极的极线:反之,极线必定是大圆弧.如果球面上某一点到其它两点(不是直 径的两个端点)的球面距离均为90°,则前一点必是通过后两点的大圆的极。对一个圆而言, 轴、极必定是成对而出现的:而极和极线也是成对出现的。两个大圆的极之间的大圆弧所对 的球心角等于此两大圆平面的二面角。 4.1.5球面角及其度量 球面上两个大圆弧所构成的角称为球面角。两大圆弧的交点称为球面角的顶点,大圆 弧称为球面角的边, 球面角的大小由这两个大圆弧平面所构成的二面角来确定.球面角的度量方法: 1、作两条边的切线取其夹角(平面角): 2、顶点的极线被球面角两边所截的弧长 3、该弧长所对的球心角
77 图 4.1.1 图 4.1.2 4.1.3 球面距离 球面上一个大圆的长是 0 360 ,球面上两点 A 、B 间小于 0 180 的大圆弧(也称劣弧)长 称为球面距离,它是点 A 、 B 间的最短球面距离,在航海上称为大圆航线. 地球半径大约 为 6370 km. 海上距离的单位是海里,即把地球子午线上 1 的弧长称为 1 n mile. 其换算公 式是 1 n mile =1852 m. 4.1.4 轴、极、极距、极线 垂直于任一圆的球直径称为该圆的轴,轴与球面的两个交点称为极,显然,球上任一个 圆都有两个极. 从大圆弧或小圆弧上的一点到极的球面距离称为极距. 因为同圆上任意一 点的极距都相等,所以也可以称极为该圆的球面中心,称极距为该圆的球面半径. 注:球面中心不是圆心;球面半径不是球半径. 极距等于 0 90 的大圆弧称为极线或称为赤道. 因为任一大圆与其极的极距为 0 90 ,所以 大圆弧是它的极的极线;反之,极线必定是大圆弧. 如果球面上某一点到其它两点(不是直 径的两个端点)的球面距离均为 0 90 ,则前一点必是通过后两点的大圆的极. 对一个圆而言, 轴、极必定是成对而出现的;而极和极线也是成对出现的. 两个大圆的极之间的大圆弧所对 的球心角等于此两大圆平面的二面角. 4.1.5 球面角及其度量 球面上两个大圆弧所构成的角称为球面角. 两大圆弧的交点称为球面角的顶点,大圆 弧称为球面角的边. 球面角的大小由这两个大圆弧平面所构成的二面角来确定. 球面角的度量方法: 1、作两条边的切线取其夹角(平面角); 2、顶点的极线被球面角两边所截的弧长; 3、该弧长所对的球心角

注:极线上的弧长与其所对的球面角同度:球面角的取值范围是0°-360° 4.1.6小圆弧长与大圆弧长之比 圆心角相等的小圆弧长与大圆弧长之比等于小圆极距的正弦或小圆纬度的余弦。即 s如Pa=b=6os4a,如图41.3示 AB 0 4.1.7地球上的基本知识 地球的第一近似体为圆球体,其半径约为6370km, 地球的自转轴称为地轴,地球绕地轴自西向东转。我们可0 由右手法则确定南北极。南北极的极线称为赤道。赤道将 A 地球分为南北两个相等的半球 图41.3 地球南北极与某地A所连成的大圆称为A地的子午圈,通过英国格林尼治天文台的子 午圈称为格林子午圈:连接地球南北极和某地A之间的半个大圆称为A地的午圈(子午线 或经线).在赤道上由格林午圈至A地午圈之间的弧长称为A地的经度.经度相同的点的 轨迹是午圈。位于东半球的称为东经:反之称为西经.东西经的取值范围均是0°-180°, 在A地午圈上由赤道到该地的弧长称为A地的纬度.纬度相同的点的轨迹是平行于赤 道的小圆,该小圆称为纬度圈或等纬圈。纬度越高,等纬圈的长度越短。若A地位于南半 球,称之为南纬,反之称为北纬。南北纬的取值范围均是0°-90°. 在航海上,A地的坐标通常用4(@,)表示,其中p是纬度,入是经度。 例1设某船由A(60N,100°E),向东航行至B(60°N,103E),求AB的距离, 解由4.1.6知,在赤道上,103°-100°-3°×60=180nmi1e,所以 B =180xcos60=90n mile. 即当纬度为60时,等纬圈的长度仅为赤道长度的一半. 例2设两船同在北纬30°N,相距600 n mile,若它们以同速向北航行1800 n mile,求两 船相距多少海里? 600 解由416知,两船在赤道上的距离为c0s30=4005a■i1e, 向北航行1800 n mile,即30°,到达北纬60°N,所以两船相距
78 注:极线上的弧长与其所对的球面角同度;球面角的取值范围是 0 0 0 360 − . 4.1.6 小圆弧长与大圆弧长之比 圆心角相等的小圆弧长与大圆弧长之比等于小圆极距的正弦或小圆纬度的余弦. 即 sin cos ab Pa Aa AB = = ,如图 4.1.3 示. 4.1.7 地球上的基本知识 地球的第一近似体为圆球体,其半径约为 6370 km, 地球的自转轴称为地轴,地球绕地轴自西向东转. 我们可 由右手法则确定南北极. 南北极的极线称为赤道. 赤道将 地球分为南北两个相等的半球. 地球南北极与某地 A 所连成的大圆称为 A 地的子午圈,通过英国格林尼治天文台的子 午圈称为格林子午圈;连接地球南北极和某地 A 之间的半个大圆称为 A 地的午圈(子午线 或经线). 在赤道上由格林午圈至 A 地午圈之间的弧长称为 A 地的经度. 经度相同的点的 轨迹是午圈. 位于东半球的称为东经;反之称为西经. 东西经的取值范围均是 0 0 0 180 − . 在 A 地午圈上由赤道到该地的弧长称为 A 地的纬度. 纬度相同的点的轨迹是平行于赤 道的小圆,该小圆称为纬度圈或等纬圈. 纬度越高,等纬圈的长度越短. 若 A 地位于南半 球,称之为南纬,反之称为北纬. 南北纬的取值范围均是 0 0 0 90 − . 在航海上, A 地的坐标通常用 A(,) 表示,其中 是纬度, 是经度. 例 1 设某船由 0 0 A N E (60 ,100 ) ,向东航行至 0 0 B N E (60 ,103 ) ,求 AB 的距离. 解 由 4.1.6 知,在赤道上, 0 0 0 103 100 3 − = = 60 180 n mile,所以 AB 0 = = 180 cos60 90 n mile. 即当纬度为 0 60 时,等纬圈的长度仅为赤道长度的一半. 例 2 设两船同在北纬 0 30 N ,相距 600 n mile,若它们以同速向北航行 1800 n mile,求两 船相距多少海里? 解 由 4.1.6 知,两船在赤道上的距离为 0 600 400 3 cos30 = n mile, 向北航行 1800 n mile,即 0 30 ,到达北纬 0 60 N ,所以两船相距 图 4.1.3 A a P b B 0 0

400√5.cos60°=200√5nmi1e 注:1、子午圈,午圈,子午线,经线指南北向:纬度圈,等纬圈指东西向。 2、午圈上所有点的经度相同:纬度圈上所有点的纬度相同。 练习题4.1 1、是非题 (1)小球分球为相等的两部分 (②)过球面上在同一直径两端的两点,只能作一个大圆: (3)球面上两点间小于180°圆弧的长是这两点间的最短球 面距离: (4④地球子午线上1”的弧长称为1海里: (⑤)极到极线的球面距离为90°: (6)极距是指任一点到子午线上的球面距离: (7)球面半径与球半径相等: (⑧)球面角与其所对应的大圆弧长相等: 图4.1.4 (⑨)纬度是指地球上某点到北(南)极的球面距离。 2.如图4.1.4所示,球面上的p,为地球北极,弧gcd为赤道,弧aeb为等纬圈。设cd长 200 n mile,e点的纬度为45°,求ef长(n mile)? 3.设某船由A(0°N,100°E)向东航行120 n mile,后沿子午圈向北航行3600 n mile,再转 向沿等纬圈向西航行120 n mile,最后转向沿子午圈向南航行3600 n mile,求: (1)船舶最后到达点的纬度:(2)起航点与到达点相距多少海里? 4.设A船位于(60°V,100°E),B船位于(60°N,120°E),若两船以同速向南航行 则它们在航行3600海里后相距多少海里? 5.设两船同在北纬30°N,相距600 n mile,若它们以同速向北航行900 n mile,则两船 相距多少海里?
79 0 400 3 cos60 200 3 = n mile. 注:1、子午圈,午圈,子午线,经线指南北向;纬度圈,等纬圈指东西向. 2、午圈上所有点的经度相同;纬度圈上所有点的纬度相同. 练习题 4.1 1、是非题 (1)小球分球为相等的两部分; (2)过球面上在同一直径两端的两点,只能作一个大圆; (3)球面上两点间小于 0 180 圆弧的长是这两点间的最短球 面距离; (4)地球子午线上 1 的弧长称为 1 海里; (5)极到极线的球面距离为 0 90 ; (6)极距是指任一点到子午线上的球面距离; (7)球面半径与球半径相等; (8)球面角与其所对应的大圆弧长相等; (9)纬度是指地球上某点到北(南)极的球面距离. 2.如图 4.1.4 所示,球面上的 n p 为地球北极,弧 qcdq 为赤道,弧 aefb 为等纬圈. 设 cd 长 200 n mile,e 点的纬度为 0 45 ,求 ef 长(n mile)? 3.设某船由 0 0 A N E (0 ,100 ) 向东航行 120 n mile,后沿子午圈向北航行 3600 n mile,再转 向沿等纬圈向西航行 120 n mile,最后转向沿子午圈向南航行 3600 n mile,求: (1)船舶最后到达点的纬度;(2)起航点与到达点相距多少海里? 4.设 A 船位于( 0 60 N 0 ,100 E ), B 船位于( 0 60 , N 0 120 E ),若两船以同速向南航行, 则它们在航行 3600 海里后相距多少海里? 5.设两船同在北纬 0 30 N ,相距 600 n mile,若它们以同速向北航行 900 n mile,则两船 相距多少海里? 图 4.1.4

4.2球面三角 4.2.1球面三角形的定义 球面上由三个大圆弧相交于三点所围成的球面部分称为球面三角形.称这三个大圆弧 为球面三角形的边,这三点为球面三角形的项点,由任意两个大圆弧所构成的球面角称为球 面三角形的角。 三边和三个角称为球面三角形六要素。三边用a,b,c表示,三个角用A,B,C 表示,它们的取值范围均是0°-360°.六要素的取值范围均是0°-180°的球面三角形称为 欧拉球面三角形.本书仅讨论欧拉球面三角形 4.2.2球面三角形的分类 1、球面直角(边)三角形 至少有一个角(边)为90°的球面三角形称为球面直角(边)三角形。 2、球面等腰三角形和球面等边三角形 两边或两角相等的球面三角形称为球面等腰三角形:三边或三角相等的球面三角形称为 球面等边三角形. 3、球面初等三角形 相对于球半径三边都非常小的球面三角形称为球面小三角形:一个边和对角相对于其他 两边及其对角都很小的球面三角形称为球面窄三角形.球面小三角形和球面窄三角形统称 为球面初等三角形 4、球面任意三角形 不属于以上三类的球面三角形称为球面任意三角形, 注:球面直角(边)三角形可以是两个角(边)或三个角(边)为90°,这个特点不同于平 面三角形, 4.2.3两个球面三角形的关系 1、全等球面三角形 在同球和等球面上,边角对应相等且排列顺序相同的球面三角形称为全等球面三角形. 2、对称球面三角形 在同球和等球面上,边角对应相等且排列顺序相反的球面三角形称为对称球面三角形 如图4.2.1示
80 4.2 球面三角 4.2.1 球面三角形的定义 球面上由三个大圆弧相交于三点所围成的球面部分称为球面三角形. 称这三个大圆弧 为球面三角形的边,这三点为球面三角形的顶点,由任意两个大圆弧所构成的球面角称为球 面三角形的角. 三边和三个角称为球面三角形六要素. 三边用 a ,b ,c 表示,三个角用 A ,B ,C 表示,它们的取值范围均是 0 0 0 360 − . 六要素的取值范围均是 0 0 0 180 − 的球面三角形称为 欧拉球面三角形. 本书仅讨论欧拉球面三角形. 4.2.2 球面三角形的分类 1、球面直角(边)三角形 至少有一个角(边)为 0 90 的球面三角形称为球面直角(边)三角形. 2、球面等腰三角形和球面等边三角形 两边或两角相等的球面三角形称为球面等腰三角形;三边或三角相等的球面三角形称为 球面等边三角形. 3、球面初等三角形 相对于球半径三边都非常小的球面三角形称为球面小三角形;一个边和对角相对于其他 两边及其对角都很小的球面三角形称为球面窄三角形. 球面小三角形和球面窄三角形统称 为球面初等三角形. 4、球面任意三角形 不属于以上三类的球面三角形称为球面任意三角形. 注:球面直角(边)三角形可以是两个角(边)或三个角(边)为 0 90 ,这个特点不同于平 面三角形. 4.2.3 两个球面三角形的关系 1、全等球面三角形 在同球和等球面上,边角对应相等且排列顺序相同的球面三角形称为全等球面三角形. 2、对称球面三角形 在同球和等球面上,边角对应相等且排列顺序相反的球面三角形称为对称球面三角形. 如图 4.2.1 示
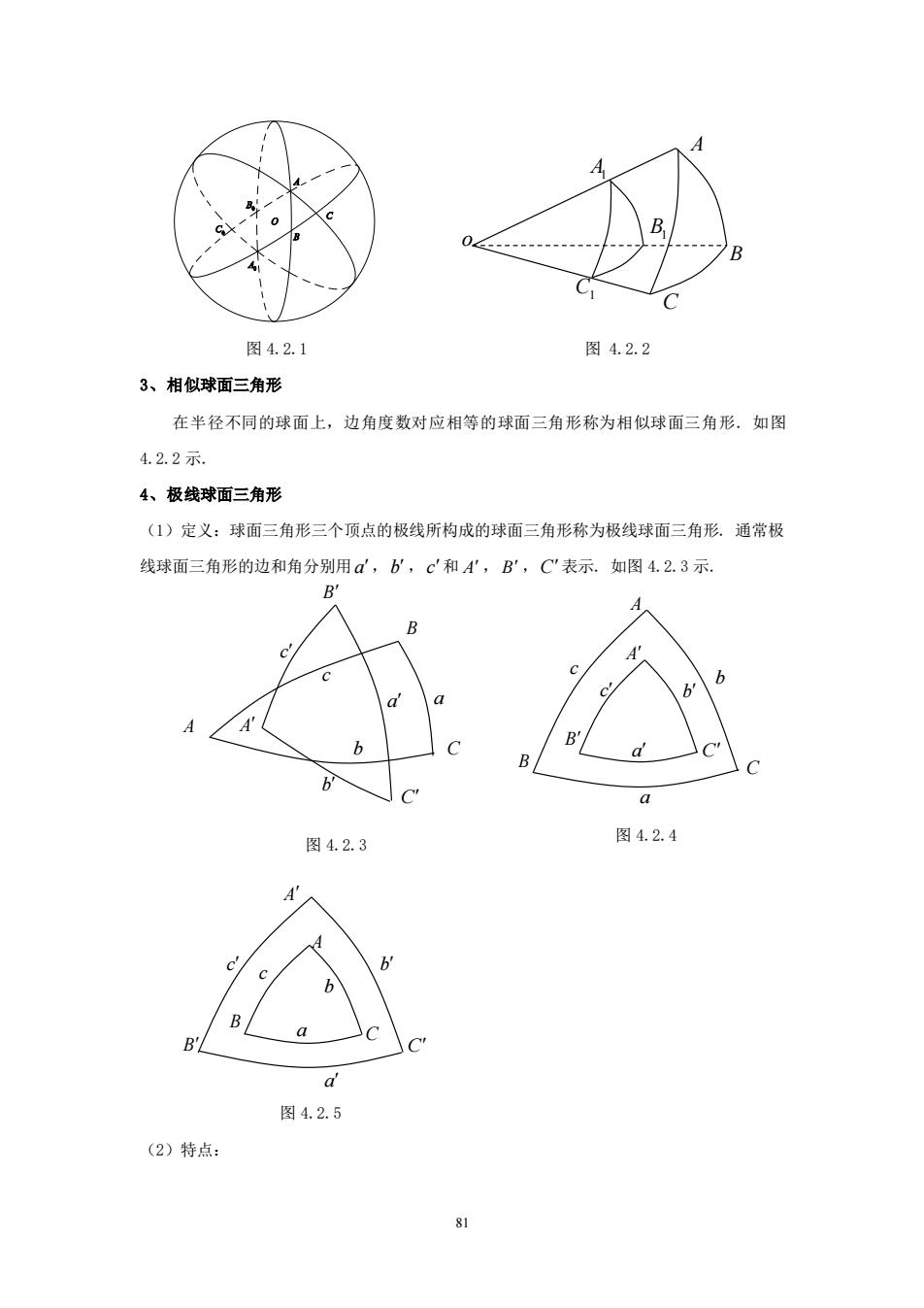
图4.2.1 图4.2.2 3、相似球面三角形 在半径不同的球面上,边角度数对应相等的球面三角形称为相似球面三角形.如图 4.2.2示. 4、极线球面三角形 (1)定义:球面三角形三个顶点的极线所构成的球面三角形称为极线球面三角形.通常极 线球面三角形的边和角分别用d,b,c'和A',B',C表示.如图42.3示. 图4.2.3 图4.2.4 图4.2.5 (2)特点:
81 图 4.2.1 图 4.2.2 3、相似球面三角形 在半径不同的球面上,边角度数对应相等的球面三角形称为相似球面三角形. 如图 4.2.2 示. 4、极线球面三角形 (1)定义:球面三角形三个顶点的极线所构成的球面三角形称为极线球面三角形. 通常极 线球面三角形的边和角分别用 a ,b ,c 和 A , B ,C 表示. 如图 4.2.3 示. (2)特点: o A B1 C1 A1 B C A B C A B C 图 4.2.4 a c b b a c A B C A B C 图 4.2.5 a a b c b c A A B B C C 图 4.2.3 c c b b a a

①若原球面三角形的三边都大于90°,则极线球面三角形在原球面三角形内:如图4.2.4示 ②若原球面三角形的三边都小于90°,则极线球面三角形在原球面三角形外:如图4.2.5示 ③若原球面三角形的一边或两边大于90°,则极线球面三角形与原球面三角形交叉形成。如 图4.2.3示. (3)关系: ①原球面三角形与极线球面三角形是相互的关系,即原球面三角形的顶点是极线球面三角形 对应边的极:反之,极线球面三角形的顶点是原球面三角形对应边的极。 ②原三角形的角(边)与极线球面三角形的边(角)互补.即 a+=180°,d+A=180°, b+B=180°,b+B=180°, c+C'=180°,c+C=180° 注:全等球面三角形与平面三角形全等的条件一样 4.2.4球面三角形的性质 1、球面三角形与三面角的关系 球面三角形与三面角之间可以相互度量,有如下的关系。如图4.2.6示 (1)球心是三面角的顶点: (2)球半径是三面角的棱: (3)球面三角形的边是三面角的平面角: (4)球面三角形的角是三面角的二面角, 02 2、球面三角形的边 (1)三边都是大圆弧,且0°<每一边<180° 图4.2.6 (2)两边之和大于第三边,两边之差小于第三边,如a-b<c<a+: (3)三边之和大于0°且小于360°,即0°<a+b+c<360°. 3、球面三角形的角 (1)0°<每-一角<180° (2)三角之和大于180°小于540°,即180°<A+B+C<540°
82 ①若原球面三角形的三边都大于 0 90 ,则极线球面三角形在原球面三角形内;如图 4.2.4 示. ②若原球面三角形的三边都小于 0 90 ,则极线球面三角形在原球面三角形外;如图 4.2.5 示. ③若原球面三角形的一边或两边大于 0 90 ,则极线球面三角形与原球面三角形交叉形成. 如 图 4.2.3 示. (3)关系: ①原球面三角形与极线球面三角形是相互的关系,即原球面三角形的顶点是极线球面三角形 对应边的极;反之,极线球面三角形的顶点是原球面三角形对应边的极. ②原三角形的角(边)与极线球面三角形的边(角)互补. 即 0 a A + = 180 , 0 a A + =180 , 0 b B+ = 180 , 0 b B + =180 , 0 c C+ = 180 , 0 c C + =180 . 注:全等球面三角形与平面三角形全等的条件一样. 4.2.4 球面三角形的性质 1、球面三角形与三面角的关系 球面三角形与三面角之间可以相互度量,有如下的关系. 如图 4.2.6 示. (1)球心是三面角的顶点; (2)球半径是三面角的棱; (3)球面三角形的边是三面角的平面角; (4)球面三角形的角是三面角的二面角. 2、球面三角形的边 (1)三边都是大圆弧,且 0 0 < 每一边 0 <180 ; (2)两边之和大于第三边,两边之差小于第三边,如 a −b c a +b ; (3)三边之和大于 0 0 且小于 0 360 ,即 0 0 0 < <360 abc + + . 3、球面三角形的角 (1) 0 0 < 每一角 0 <180 ; (2))三角之和大于 0 180 小于 0 540 ,即 0 0 180 < <540 A B C + + ; o A B1 C1 A1 B C 图 4.2.6 b c a

(3)两角之和减去第三角小于180°,如A+B-C180°,球面三角形不存在。 2.a=100°,b=170°,c=70°. 解a+c-170°-b,球面三角形不存在 3.A=100°,B=100°,C=100° 解满足已知三角的三个条件,“球面三角形存在
83 (3)两角之和减去第三角小于 0 180 ,如 0 A B C + − 180 ; (4)两角之和(差)大于(小于)第三角的外角,如 A − B D A + B . 如图 4.2.7 示. 4、边与角 (1)等边对等角,等角对等边; (2)大(小)边对大(小)角,大(小)角对大(小) 边. 4.2.5 球面三角形成立的条件 1、已知球面三角形的三个边时: (1) 0 0 < 每一边 0 <180 ; (2) 0 0 0 < <360 abc + + ; (3)两边之和大于第三边,两边之差小于第三边. 2、已知球面三角形的三个角时: (1) 0 0 < 每一角 0 <180 ; (2) 0 0 180 < <540 A B C + + ; (3)两角之和减去第三角小于 0 180 . 3、若给定球面三角形的两个角(边)及其夹边(角),则仅需满足每一个角和每一个边大于 0 0 ,小于 0 180 的条件,球面三角形都成立. 注: c 边和 C 角在写法上的区别. 例 判断下面的球面三角形是否存在. 1. 0 A =100 , 0 B =170 , 0 C = 70 . 解 ∵ 0 0 A B C + − = 200 180 ,∴球面三角形不存在. 2. 0 a =100 , 0 b =170 , 0 c = 70 . 解 ∵ 0 a c b + = = 170 ,∴球面三角形不存在. 3. 0 A =100 , 0 B =100 , 0 C =100 . 解 ∵ 满足已知三角的三个条件,∴球面三角形存在. 图 4.2.7

4.a=100°,b=100°,c=100 解:满足已知三边的三个条件,“球面三角形存在 5.a=170°,b=170°,C=170°. 解:两个边及其夹角,都满足大于0°,小于180的条件,“球面三角形存在 练习题4.2 1.是非题 (1)球面直边三角形是指只有一个边为90°的球面三角形: (②)在同球上,边角对应相等的球面三角形称为球面全等三角形: (3)球面三角形三边之和大于0°,小于540°: (④球面三角形两角之和必小于第三角: (⑤)球面三角形外角小于相邻的两内角之和. 2.由极线上任一点和极线相连的大圆弧与极线构成怎样的球面角? 3.已知一球面三角形三个角分别为90°、90°、60°,试问该球面三角形的三边各为何值? 4.判断新下列球面三角形是否存在: (1)a=110°,b=60°,c=50°:(2)A=110°,B=60°,C=50°: (3)a=120°,b=120,c=120:(4)A=120°,B=120°,C=120° (5)a=100°,b=170°,c=90°:(6)A=100°,B=170°,C=90°: (7)a=60°,b=60°,c=60°:(8)A=60°,B=60°,C=60°: (9)a=1°,B=179°,c=179°:(10)A=28°,b=179°,C=181° 5.设球面三角形ABC的三边为a、b、c,且a>b>c,它的极线三角形的三边为d、b、 c,求证:dC,求证: (1)2700>B+C>90°:(2)B-C<90°. 7.在球面三角形ABC中,设a=90°,求证:
84 4. 0 a =100 , 0 b =100 , 100o c = . 解 ∵ 满足已知三边的三个条件,∴球面三角形存在. 5. 0 a =170 , 0 b =170 , 0 C =170 . 解 ∵两个边及其夹角,都满足大于 0 0 ,小于 0 180 的条件,∴球面三角形存在. 练习题 4.2 1. 是非题 (1)球面直边三角形是指只有一个边为 0 90 的球面三角形; (2)在同球上,边角对应相等的球面三角形称为球面全等三角形; (3)球面三角形三边之和大于 0 0 ,小于 0 540 ; (4)球面三角形两角之和必小于第三角; (5)球面三角形外角小于相邻的两内角之和. 2.由极线上任一点和极线相连的大圆弧与极线构成怎样的球面角? 3.已知一球面三角形三个角分别为 0 90 、 0 90 、 0 60 ,试问该球面三角形的三边各为何值? 4.判断下列球面三角形是否存在: (1) 0 a =110 , 0 b = 60 , 0 c = 50 ; (2) 0 A =110 , 0 B = 60 , 0 C = 50 ; (3) 0 a =120 , 0 b =120 , 0 c =120 ; (4) 0 A =120 , 0 B =120 , 0 C =120 ; (5) 0 a =100 , 0 b =170 , 0 c = 90 ; (6) 0 A =100 , 0 B =170 , 0 C = 90 ; (7) 0 a = 60 , 0 b = 60 , 0 c = 60 ; (8) 0 A = 60 , 0 B = 60 , 0 C = 60 ; (9) 0 a =1 , 0 B =179 , 0 c =179 ; (10) 0 A = 28 , 0 b =179 , 0 C =181 . 5.设球面三角形 ABC 的三边为 a、b 、c ,且 abc ,它的极线三角形的三边为 a 、b 、 c ,求证: abc . 6.在球面三角形 ABC 中,设 0 A = 90 ,且 B C ,求证: (1) 0 0 270 90 + B C ;(2) 0 B C− 90 . 7. 在球面三角形 ABC 中,设 0 a = 90 ,求证:

(1)270°>b+c>90°:(2)b-c<90° 8.在球面三角形ABC中,求证: D-90°<(4+B-C)<90:(2)0°<a+b-c<180 9.如图4.2.8,AP、BP、CP、DP、EP和ABCDE都是大圆弧,求证 ∠APB+∠BPC+∠CPD+∠DPE+∠EPA=36O° 图4.2.8 图4.2.9 10.如图4.2.9,球面上P点是大圆弧QER的极,Z点是大圆弧SEN的极,求证 (1)SE=EN=QE=ER=90°:(2)ZP=SQ,OZ=PN. 4.3球面三角形公式 4.3.1余弦公式 1、边的余弦公式: 球面三角形一个边的余弦等于其它两边余弦的乘积加上这两边正弦及其夹角余弦的乘 cosa=cosbcosc+sin bsin ccos d cosb=cos a cosc+sin asin ccos B (4.3.1) cosc=cosacosb+sin asin bcosC 公式(4.3.1)通常用于求解已知两边及其夹角求第三边或者已知三边求一角。它在航海 实际工作中是最常用的公式之一,如求起航点与到达点之间的距离。 2、角的余弦公式 球面三角形一个角的余弦等于其它两角余弦的乘积冠以负号加上这两角正弦及其夹边 女
85 (1) 0 0 270 90 + b c ;(2) 0 b c − 90 . 8.在球面三角形 ABC 中,求证: (1) ( ) 0 0 1 90 90 2 − + − A B C ;(2) ( ) 0 0 1 0 180 2 + − a b c . 9. 如图 4.2.8, AP 、 BP 、CP 、 DP、 EP 和 ABCDE 都是大圆弧,求证: 0 + + + + = APB BPC CPD DPE EPA 360 . 图 4.2.8 图 4.2.9 10.如图 4.2.9,球面上 P 点是大圆弧 QER 的极, Z 点是大圆弧 SEN 的极,求证: (1) 0 SE EN QE ER = = = = 90 ;(2) ZP SQ = ,QZ PN = . 4.3 球面三角形公式 4.3.1 余弦公式 1、边的余弦公式: 球面三角形一个边的余弦等于其它两边余弦的乘积加上这两边正弦及其夹角余弦的乘 积. = + = + = + c a b a b C b a c a c B a b c b c A cos cos cos sin sin cos cos cos cos sin sin cos cos cos cos sin sin cos (4.3.1) 公式(4.3.1)通常用于求解已知两边及其夹角求第三边或者已知三边求一角. 它在航海 实际工作中是最常用的公式之一,如求起航点与到达点之间的距离. 2、角的余弦公式: 球面三角形一个角的余弦等于其它两角余弦的乘积冠以负号加上这两角正弦及其夹边