
第六章最或是船位及误差评定 航海上,驾驶员经常观测陆标方位或距离,或者观测天体高度等来确定船位,同时根据 船位误差理论的原则采用正确的方法,对一系列的数据进行处理以提高观测结果的精度,本 章将研究最或是船位的基本理论和船位误差理论。 6.1最或是船位及其误差 6.1.1船位线 在航海定位中,测者对物标进行观测时,其观测值为常数值的点的几何轨迹,称为观测 者的位置线或等值线。航海上船位位置线是指满足某一观测值为定值的点的轨迹,它是一条 (或一对)等值线.在观测时刻,测者(船舶)的位置只可能在位置线上,在观测瞬间,船位 位置线通常以船位线来表示,即指推算船位附近位置线的一段或位置线上某点的切线的一段 航海上常见的船位线有主要有:方位船位线、距离船位线、方位差船位线、距离差船位线、 天文船位线和转移船位线等.下面主要讨论方位船位线和距离船位线. 6.1.2船位线的概念 1、方位船位线:在近距离上,是和所观测已知位置的物标具有相同方位的点的轨迹 (1)平面上:方位船位线是物标M与船位P两点间的直线(如图6.1): (2)球面上:方位船位线是趋向极点P,且通过船位P和物标M所连的恒位线(如图6.2). 图6.1 图6.2 2、距离船位线: (1)平面上:是以物标M为圆心,船位与物标的距离PM为半径的圆: (2)球面上:是以物标M为极点,船位与物标的距离PM为极距的球面小圆, 3、方位差船位线(水平角位置线):在平面上,是船位P与两物标M,M,所构成三角形 128
128 第六章 最或是船位及误差评定 航海上,驾驶员经常观测陆标方位或距离,或者观测天体高度等来确定船位,同时根据 船位误差理论的原则采用正确的方法,对一系列的数据进行处理以提高观测结果的精度,本 章将研究最或是船位的基本理论和船位误差理论. 6.1 最或是船位及其误差 6.1.1 船位线 在航海定位中,测者对物标进行观测时,其观测值为常数值的点的几何轨迹,称为观测 者的位置线或等值线. 航海上船位位置线是指满足某一观测值为定值的点的轨迹,它是一条 (或一对)等值线. 在观测时刻,测者(船舶)的位置只可能在位置线上,在观测瞬间,船位 位置线通常以船位线来表示,即指推算船位附近位置线的一段或位置线上某点的切线的一段. 航海上常见的船位线有主要有:方位船位线、距离船位线、方位差船位线、距离差船位线、 天文船位线和转移船位线等. 下面主要讨论方位船位线和距离船位线. 6.1.2 船位线的概念 1、方位船位线:在近距离上,是和所观测已知位置的物标具有相同方位的点的轨迹. (1)平面上:方位船位线是物标 M 与船位 P 两点间的直线(如图 6.1); (2)球面上:方位船位线是趋向极点 PN 且通过船位 P 和物标 M 所连的恒位线(如图 6.2). 图 6.1 图 6.2 2、距离船位线: (1)平面上:是以物标 M 为圆心,船位与物标的距离 PM 为半径的圆; (2)球面上:是以物标 M 为极点,船位与物标的距离 PM 为极距的球面小圆. 3、方位差船位线(水平角位置线):在平面上,是船位 P 与两物标 M1 , M2 所构成三角形

的外接圆圆弧的一部分(如图6.3). 4、距离差船位线:是以两物标M,M,为焦点的双曲线(如图6.4) 图6.3 图6.4 由于球面上的位置线都比较复杂,有时要把它们全部画在图上,难度较大,且没有必 要.航海人员感兴趣的是航海定位和导航,仅仅只要画出位置线在船舶附近的一小段,或 者画出这一小段位置的切线,来代表这条位置线,所以在海图作业时,通常只画出船位线, 且用船位线来代替位置线进行定位和导航。 6.1.3船位线误差 1.方位船位线误差 观测某一物标的方位船位线的系统误差ε为: 6=t590 57.3 =±s8 D.arcl° (6.1.1) 其中:a=571的度值 观测某一物标的方位船位线的随机误差σ为: 0=±gD 573 =o D.arel° (6.1.2) 其中:D为测者到物标的距离,为系统观测误差,为随机观测误差。 由系统误差和随机误差的表达式可知在观测误差6或0。一定的条件下,观测的物标越 近,船位线误差£或。越小,因此应尽量观测近物标的方位来求方位船位线 2.距离船位线误差 观测某一物标的距离船位线的系统误差为 129
129 的外接圆圆弧的一部分(如图 6.3). 4、距离差船位线:是以两物标 M1 , M2 为焦点的双曲线(如图 6.4). 图 6.3 图 6.4 由于球面上的位置线都比较复杂,有时要把它们全部画在图上,难度较大,且没有必 要. 航海人员感兴趣的是航海定位和导航,仅仅只要画出位置线在船舶附近的一小段,或 者画出这一小段位置的切线,来代表这条位置线,所以在海图作业时,通常只画出船位线, 且用船位线来代替位置线进行定位和导航. 6.1.3 船位线误差 1.方位船位线误差 观测某一物标的方位船位线的系统误差 为: 0 0 57 .3 B D = 0 0 1 = B D arc (6.1.1) 其中: 0 0 1 1 57 .3 arc = = 0 1 的弧度值. 观测某一物标的方位船位线的随机误差 为: =± 0 0 57 .3 B D = 0 0 1 B D arc (6.1.2) 其中: D 为测者到物标的距离, B 为系统观测误差, B 为随机观测误差. 由系统误差和随机误差的表达式可知在观测误差 B 或 B 一定的条件下,观测的物标越 近,船位线误差 或 越小,因此应尽量观测近物标的方位来求方位船位线. 2.距离船位线误差 观测某一物标的距离船位线的系统误差为 :
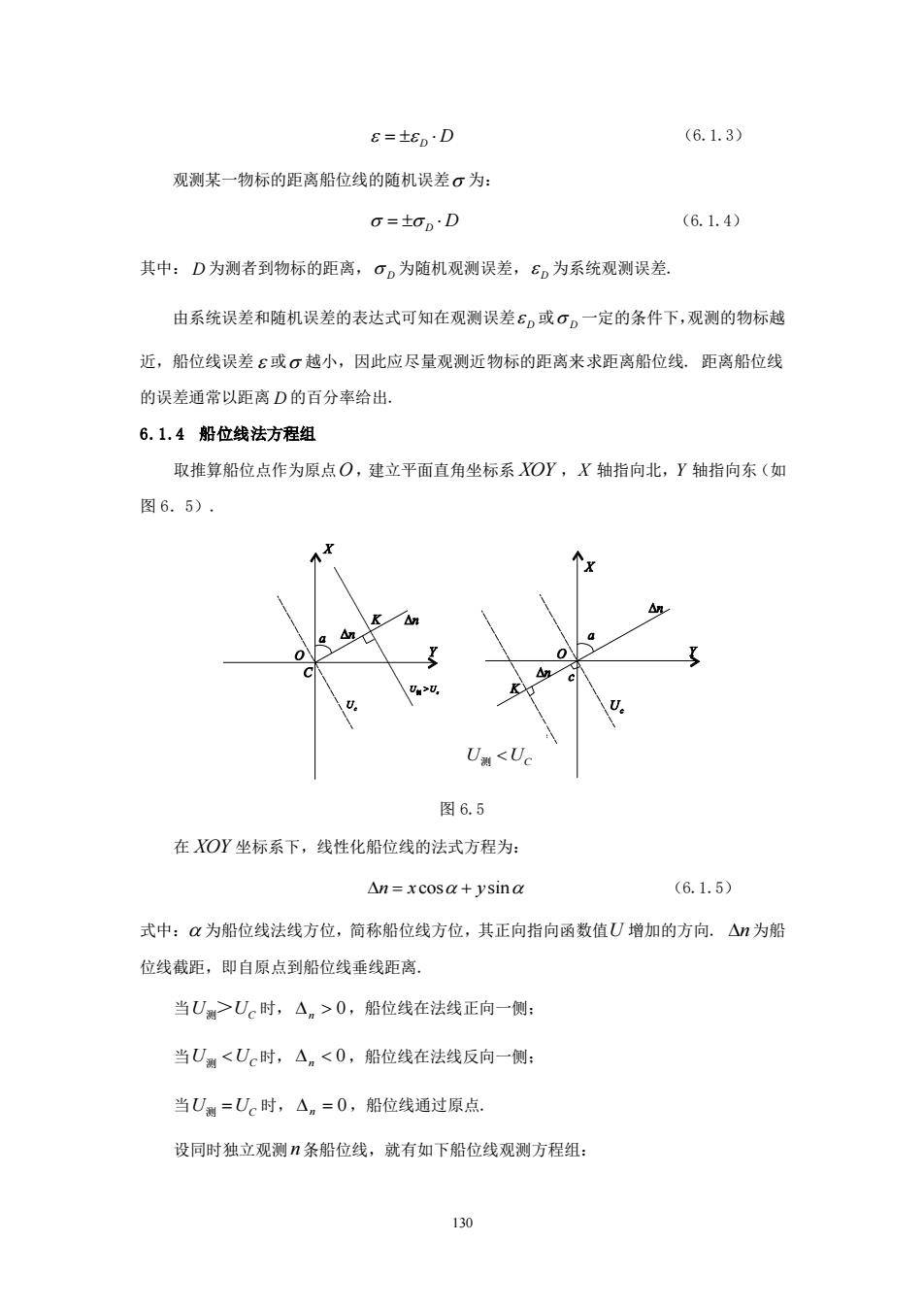
E=±8D·D (6.1.3) 观测某一物标的距离船位线的随机误差σ为: G=top.D (6.1.4) 其中:D为测者到物标的距离,口。为随机观测误差,6D为系统观测误差。 由系统误差和随机误差的表达式可知在观测误差6或0。一定的条件下,观测的物标越 近,船位线误差ε或σ越小,因此应尽量观测近物标的距离来求距离船位线。距离船位线 的误差通常以距离D的百分率给出。 6.1.4船位线法方程组 取推算船位点作为原点O,建立平面直角坐标系XOY,X轴指向北,Y轴指向东(如 图6.5). UaUc时,△.>0,船位线在法线正向一侧: 当U<Uc时,△n<0,船位线在法线反向一侧: 当U测=Uc时,△n=0,船位线通过原点 设同时独立观测条船位线,就有如下船位线观测方程组: 130
130 = D D (6.1.3) 观测某一物标的距离船位线的随机误差 为: = D D (6.1.4) 其中: D 为测者到物标的距离, D 为随机观测误差, D 为系统观测误差. 由系统误差和随机误差的表达式可知在观测误差 D 或 D 一定的条件下,观测的物标越 近,船位线误差 或 越小,因此应尽量观测近物标的距离来求距离船位线. 距离船位线 的误差通常以距离 D 的百分率给出. 6.1.4 船位线法方程组 取推算船位点作为原点 O ,建立平面直角坐标系 XOY ,X 轴指向北, Y 轴指向东(如 图 6.5). 图 6.5 在 XOY 坐标系下,线性化船位线的法式方程为: = + n x y cos sin (6.1.5) 式中: 为船位线法线方位,简称船位线方位,其正向指向函数值 U 增加的方向. n 为船 位线截距,即自原点到船位线垂线距离. 当 U U 测> C 时, n 0 ,船位线在法线正向一侧; 当 U U 测 C 时, n 0 ,船位线在法线反向一侧; 当 U U 测 = C 时, n = 0 ,船位线通过原点. 设同时独立观测 n 条船位线,就有如下船位线观测方程组: U U 测 C

Xa+sma-M=0,A-答1-i2n22》&16 式中:△,表示第i条船位线截距,可把它理解为观测值:G,表示第i条船位线标准误差,乃 表示第条船位线权 根据船位线观测方程组,可直接得到船位线法方程组: [pcosax+[pcosasin aly=[pAncosal (6.1.7) [pcosasin ax+[psin'aly=[pAnsin al 其中:【]为高斯和,方程组(6.1.3)的解为: xIpsin'allpAncosa]-IpcosasinallpAnsin) yIpeoallpAnsina]-Ipeos@sinallpAncosa) (6.1.8) [pcosallpsina]-[pcosasina 这就是最或是船位坐标(x,y): 例设有三条独立等精度船位线: 0D%=t10,2=20,8三40 1a=0° 1=120° a=240 求最或是船位。 解由于是等精度,所以船位线法方程组为: [[cos2alx+[cosasin aly=[Ancosa] [cosasin alx+[sin2 aly=[Ansin a] 列出表6-1如下: 表6-1 coso sin a; cos2 a cosa, sin2a,An,. △n, sin a, sin a, +1.0 1 0 0 0 1 0° +2.'0 120 0.5 0.866 0.25 0.433 0.75 1.732 +4."0 240° -0.5 0.866 0.25 0.433 0.75 -3.464 0.5 1.5 -2 -1.732 由此得船位线法方程组: 3
131 cos sin 0 i i i x y n + − = , 2 i 2 i u p = ( i = 1,2, , n ,n 2 ) (6.1.6) 式中: i n 表示第 i 条船位线截距,可把它理解为观测值; i 表示第 i 条船位线标准误差, i p 表示第 i 条船位线权. 根据船位线观测方程组,可直接得到船位线法方程组: + = + = [ cos sin ] [ sin ] [ sin ] [ cos ] [ cos sin ] [ cos ] 2 2 p x p y p n p x p y p n . (6.1.7) 其中:[ ]为高斯和,方程组(6.1.3)的解为: 2 2 2 2 2 2 2 2 [ sin ][ cos ] [ cos sin ][ sin ] [ cos ][ sin ] [ cos sin ] [ cos ][ sin ] [ cos sin ][ cos ] [ cos ][ sin ] [ cos sin ] p p n p p n x p p p p p n p p n y p p p − = − − = − , (6.1.8) 这就是最或是船位坐标 ( , ) x y . 例 设有三条独立等精度船位线: (1) 1 0 1. 0 0 n = + = ,(2) 2 0 2. 0 120 n = + = ,(3) 3 0 4. 0 240 n = + = ,求最或是船位. 解 由于是等精度,所以船位线法方程组为: + = + = [cos sin ] [sin ] [ sin ] [cos ] [cos sin ] [ cos ] 2 2 x y n x y n 列出表 6-1 如下: 表 6-1 i n i i cos i sin i 2 cos i cos i sin i 2 sin ni i cos ni i sin 1 +1. 0 0 1 0 0 0 0 1 0 2 + 2. 0 120 -0.5 0.866 0.25 -0.433 0.75 -1 1.732 3 + 4. 0 240 -0.5 -0.866 0.25 0.433 0.75 -2 -3.464 [] 0.5 0 1.5 -2 -1.732 由此得船位线法方程组:

1-5=-1732'所以=4 0.5x=-2 y-1.2 6.2图解法求最或是船位 在航海实际工作中,上节根据船位线法方程组,计算出最或是船位坐标的方法过于复杂 因此,有必要利用几何的方法求最或是船位。下面只介绍中心图解法 6.2.1中心图解法 对最或是船位坐标公式(6.1.4)作适当变换,可得如下关系式: ∑∑P[p四 X= ∑P,Wp四 (6.2.1) y=- ∑∑PD P=p.p,sin'(a-a). (6.2.2) 式中:P,为第1,j两条船位线交点权:a,C,表示第1,j两条船位线的方位角:P,P,表 示第1,j两条船位线的权:x,y表示第1,j两条船位线的交点坐标.其中 sin(a,-a) (6.2.3) = △n,cosa,-△n,cosa cos(a-a,) 公式(6.2.1)与力学中求质点系质心坐标的公示相比较,形式上完全一样.这样,如 将第1,广两条船位线的交点M看作具有质量P的质点,则这样一个质点系的质心位置就 是我们要确定的最或是船位。而当M,位置和P,数值已知时,我们便可用图解法求出船位。 因此,此法被称为中心图解法 例如图6,2.1所示,用中心图解法确定最或是船位 132
132 = − = − 1.5 1.732 0.5 2 y x ,所以 = − = − 1.2 4 y x . 6.2 图解法求最或是船位 在航海实际工作中,上节根据船位线法方程组,计算出最或是船位坐标的方法过于复杂. 因此,有必要利用几何的方法求最或是船位. 下面只介绍中心图解法. 6.2.1 中心图解法 对最或是船位坐标公式(6.1.4)作适当变换,可得如下关系式: [ ] [ ] [ ] [ ] ij ij i j ij i j ij ij i j ij i j p x px x p p p y py y p p = = = = , (6.2.1) 2 sin ( ) ij i j j i p p p = − . (6.2.2) 式中: ij p 为第 i , j 两条船位线交点权; , i j 表示第 i , j 两条船位线的方位角; , i j p p 表 示第 i , j 两条船位线的权; ij x , ij y 表示第 i , j 两条船位线的交点坐标. 其中: sin sin sin( ) cos cos cos( ) i j j i ij j i i j j i ij j i n n x n n y − = − − = − , (6.2.3) 公式(6.2.1)与力学中求质点系质心坐标的公示相比较,形式上完全一样. 这样,如 将第 i , j 两条船位线的交点 Mij 看作具有质量 ij p 的质点,则这样一个质点系的质心位置就 是我们要确定的最或是船位. 而当 Mij 位置和 ij p 数值已知时,我们便可用图解法求出船位. 因此,此法被称为中心图解法. 例 如图 6.2.1 所示,用中心图解法确定最或是船位
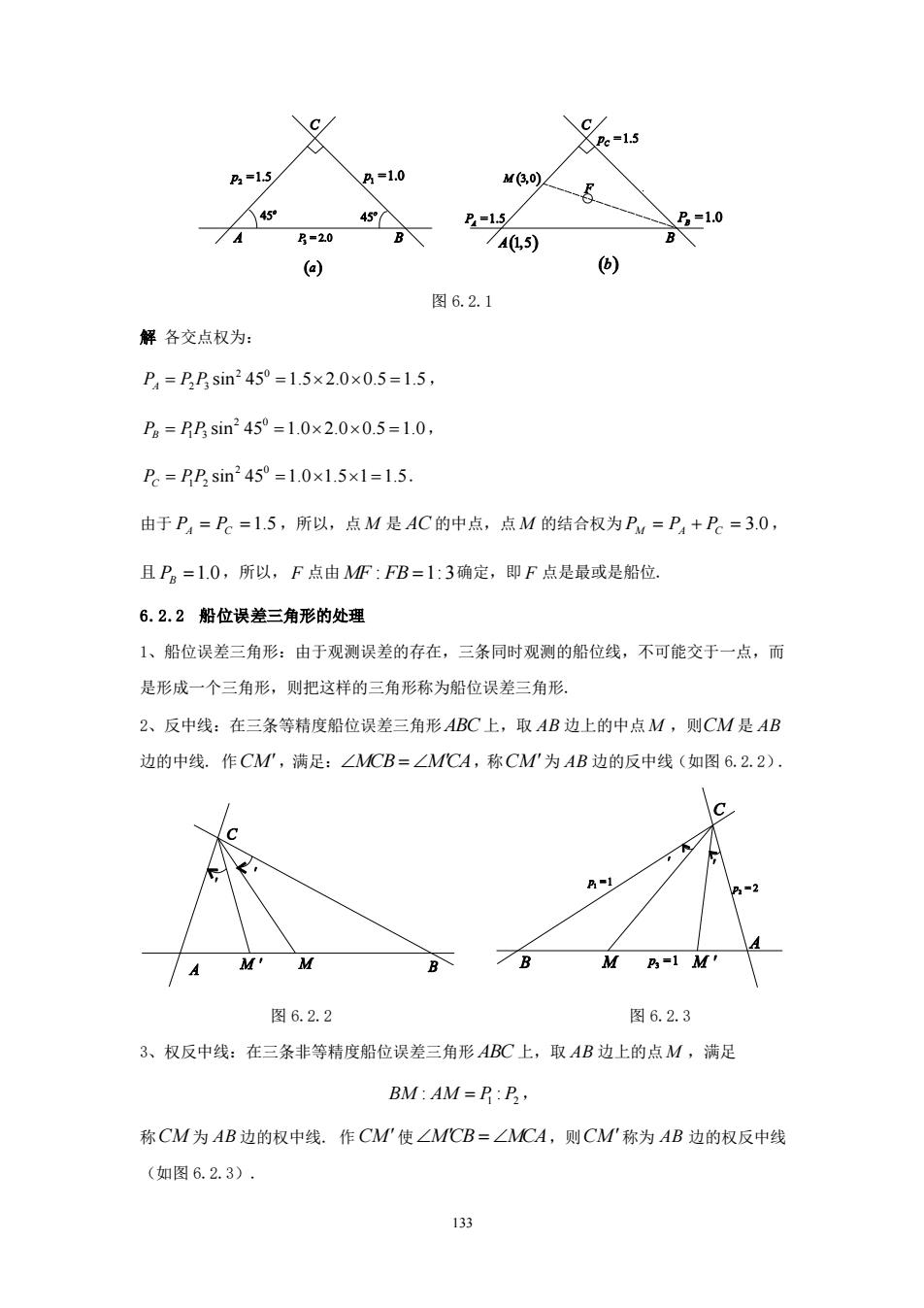
C C A=15 =1.0 Ma.o)∠ 月20 月-15 1.0 B A1,5 6) 图6.2.1 解各交点权为: P=D,Esin245°=1.5×2.0×0.5=1.5, D=PPsin245°=1.0×2.0×0.5=1.0 P=PP sin245°=1.0x1.5×1=1.5. 由于P=P=1.5,所以,点M是AC的中点,点M的结合权为P4=P4+P=3.0, 且P=1.0,所以,F点由MF:FB=1:3确定,即F点是最或是船位 6.2.2船位误差三角形的处理 1、船位误差三角形:由于观测误差的存在,三条同时观测的船位线,不可能交于一点,而 是形成一个三角形,则把这样的三角形称为船位误差三角形. 2、反中线:在三条等精度船位误差三角形ABC上,取AB边上的中点M,则CM是AB 边的中线。作CM',满足:∠MCB=∠MCA,称CM'为AB边的反中线(如图6.2.2) C A M' B M P-1 M' 图6.2.2 图6.2.3 3、权反中线:在三条非等精度船位误差三角形ABC上,取AB边上的点M,满足 BM:AM=P:P, 称CM为AB边的权中线.作CM'使∠MCB=∠MCA,则CM'称为AB边的权反中线 (如图6.2.3) 133
133 图 6.2.1 解 各交点权为: 2 0 2 3 sin 45 1.5 2.0 0.5 1.5 P P P A = = = , 2 0 1 3 sin 45 1.0 2.0 0.5 1.0 P PP B = = = , 2 0 1 2 sin 45 1.0 1.5 1 1.5 P PP C = = = . 由于 PA = PC =1.5 ,所以,点 M 是 AC 的中点,点 M 的结合权为 PM = PA + PC = 3.0, 且 PB =1.0 ,所以, F 点由 MF : FB =1: 3 确定,即 F 点是最或是船位. 6.2.2 船位误差三角形的处理 1、船位误差三角形:由于观测误差的存在,三条同时观测的船位线,不可能交于一点,而 是形成一个三角形,则把这样的三角形称为船位误差三角形. 2、反中线:在三条等精度船位误差三角形 ABC 上,取 AB 边上的中点 M ,则 CM 是 AB 边的中线. 作 CM ,满足: = MCB MCA ,称 CM 为 AB 边的反中线(如图 6.2.2). 图 6.2.2 图 6.2.3 3、权反中线:在三条非等精度船位误差三角形 ABC 上,取 AB 边上的点 M ,满足 1 2 BM AM P P : : = , 称 CM 为 AB 边的权中线. 作 CM 使 = MCB MCA ,则 CM 称为 AB 边的权反中线 (如图 6.2.3)

如果三条船位线只含有随机误差,由中心图解法一般原理可得:最或是船位是误差三角 形各边权反中线的交点:特别地,当三条船位线等精度时,最或是船位是各边反中线的交点。 设有三条船位线等精度(如图6.2.2),在△M4CM和△BCM中,由正弦定理得: CM sin A CM sinA AM sin∠ACM'BM=sin∠BCM' AM-sin B sin∠4CM BM sinA sin∠BCM 因为M是侣边的中点,所品,即 sin∠4CM sinA (△) sin∠BCM sin B 同理,在△4CM'和△BCM中,由正弦定理得: AM'_sin B sin.∠ACM BM'sin A'sin.∠BCM 因为CM是AB边的反中线,所以∠ACM=∠BCM,∠BCM=∠ACM,由此得: AM'_sin B sin∠BCM BM'sin A'sin∠ACM 由式(△),可得 AM'sin2B P BM sinA P. 所以 AM'.P.=BM'.Pa. 这正是A,B两点按权结合于M点的条件.AB边的反中线CM是最或是船位的轨 迹.三条反中线的交点当然就是最或是船位了. 同理可证,三条权反中线的交点是最或是船位。 中心图解法的主要优点是: (1)适用于任意非等精度独立船位线求最或是船位的一般方法: (2)具有明显的力学意义,几何上非常直观,避免繁琐的数学解析计算 中心图解法的主要缺点是:当船位线数目n较大时,交点数目C:=-将迅速增 2 多 当然,航海实际应用中,一般不超过4,又当某些交点权相对较小时(尤其交角很小 的交点权),可以忽略不计,以简化作图。 学习中心图解法的意义还在于,在严格的方法指导下,经过一定的实践,可以用目测 估计的方法确定最或是船位。在船位线等精度的情况下有如下的结论: 134
134 如果三条船位线只含有随机误差,由中心图解法一般原理可得:最或是船位是误差三角 形各边权反中线的交点;特别地,当三条船位线等精度时,最或是船位是各边反中线的交点. 设有三条船位线等精度(如图 6.2.2),在 ACM 和 BCM 中,由正弦定理得: sin sin CM A AM ACM = , sin sin CM A BM BCM = , sin sin . sin sin AM B ACM BM A BCM = , 因为 M 是 AB 边的中点,所以 1 AM BM = ,即 sin sin sin sin ACM A BCM B = . (△) 同理, 在 ACM BCM 和 中 ,由正弦定理得: sin sin . sin sin AM B ACM BM A BCM = , 因为 CM 是 AB 边的反中线,所以 = ACM BCM , = BCM ACM ,由此得: sin sin . sin sin AM B BCM BM A ACM = , 由式(△),可得 2 2 sin sin B A AM B P BM A P = = , 所以 AM P BM P A B = . 这正是 A , B 两点按权结合于 M 点的条件. AB 边的反中线 CM 是最或是船位的轨 迹. 三条反中线的交点当然就是最或是船位了. 同理可证,三条权反中线的交点是最或是船位. 中心图解法的主要优点是: (1)适用于任意非等精度独立船位线求最或是船位的一般方法; (2)具有明显的力学意义,几何上非常直观,避免繁琐的数学解析计算. 中心图解法的主要缺点是:当船位线数目 n 较大时,交点数目 2 n n( 1) 2 n C − = 将迅速增 多. 当然,航海实际应用中, n 一般不超过 4 ,又当某些交点权相对较小时(尤其交角很小 的交点权),可以忽略不计,以简化作图. 学习中心图解法的意义还在于,在严格的方法指导下,经过一定的实践,可以用目测 估计的方法确定最或是船位. 在船位线等精度的情况下有如下的结论:

(1)如果误差三角形是等边三角形,则最或是船位位于三角形中心(图6.2.4): (2)如果误差三角形是等腰三角形,则最或是船位位于三角形短边附近(图6.2.4): (3)如果误差三角形是直角三角形,则最或是船位位于直角附近(图6.2.4c)片 (4)如果误差三角形是一狭长三角形,可将最或是船位确定在短边中心处(图6.2.4) (5)特殊情况下,即在误差三角形附近有不明碍航物时,则需要将最或是船位确定在距碍 航物最近处(图6.2.4e) 图6.2.4 注:1、确定最或是船位,只作两条反中线或权反中线就可以: 2、如果船位误差三角形的边长平均小于2'~3时,可认为观测中只存在随机误差 6.3两条船位线的观测船位及其误差 当船舶驾驶员运用某种定位方法测得最或是船位之后,必须运用科学的方法对这个观测 船位进行系统地分析,以便掌握其可靠的和可能的分布情况,从而保证船舶安全迅速航行 6.3.1船位误差带和船位误差四边形 1.最或是船位 两条船位线的交点即是最或是船位(最接近真实船位的船位),该点的概率密度最大而概 率为零。真实船位离最概率船位越近,出现的概率就越大,反之,其概率就越小, 2、船位误差带 因为每条船位线均含有误差,且误差属于向量误差,即有大小和方向。航海上常用船位 误差带来描述船位线的误差,即以船位线为中心线左右±0(σ为船位线标准误差)的区域 称为船位误差带。真实船位落在一倍(士)、二倍(20)和三倍(士30)船位误差带内的概 率分别为68.3%、95.4%和99.7%.(如图6.3.1). 135
135 (1)如果误差三角形是等边三角形,则最或是船位位于三角形中心(图 6.2.4a); (2)如果误差三角形是等腰三角形,则最或是船位位于三角形短边附近(图 6.2.4b); (3)如果误差三角形是直角三角形,则最或是船位位于直角附近(图 6.2.4c); (4)如果误差三角形是一狭长三角形,可将最或是船位确定在短边中心处(图 6.2.4d); (5)特殊情况下,即在误差三角形附近有不明碍航物时,则需要将最或是船位确定在距碍 航物最近处(图 6.2.4e). 图 6.2.4 注:1、确定最或是船位,只作两条反中线或权反中线就可以; 2、如果船位误差三角形的边长平均小于 2 ~ 3 时,可认为观测中只存在随机误差. 6.3 两条船位线的观测船位及其误差 当船舶驾驶员运用某种定位方法测得最或是船位之后,必须运用科学的方法对这个观测 船位进行系统地分析,以便掌握其可靠的和可能的分布情况,从而保证船舶安全迅速航行. 6.3.1 船位误差带和船位误差四边形 1.最或是船位 两条船位线的交点即是最或是船位(最接近真实船位的船位),该点的概率密度最大而概 率为零。真实船位离最概率船位越近,出现的概率就越大,反之,其概率就越小. 2、 船位误差带 因为每条船位线均含有误差,且误差属于向量误差,即有大小和方向. 航海上常用船位 误差带来描述船位线的误差,即以船位线为中心线左右 c ( 为船位线标准误差)的区域 称为船位误差带. 真实船位落在一倍( )、二倍( 2 )和三倍( 3 )船位误差带内的概 率分别为 68.3%、95.4% 和 99.7%.(如图 6.3.1)

三倍标准误差四边形 二倍标准误差四边形 标准误差四边 图6.3.1 图6.3.2 超出三倍标准误差带的概率为0.3%,几乎不可能出现。因此,航海上常采用95%作 为船位误差界.真实船位相对于最概率船位分布的误差界可用三种几何图形来描述,它们分 别是船位误差四边形、船位误差椭圆和船位误差圆。 (1)船位误差四边形 设I、Ⅱ是两条同时观测到的船位线,其交点p是最或是船位.若I、Ⅱ分别存在的 标准差为±,、士02,则以士O,、±O分别所作船位线I、Ⅱ的平行线交成的四边形 ABCD称为船位误差四边形(如图6.3.2), 由它们的一倍、两倍、三倍标准误差带各自交成的平行四边形分别称为标准误差四边形。 二倍标准误差四边形、三倍标准误差四边形.根据概率的乘法公式,可得船位落入标准误差 四边形内的概率分别为: ±01、±02:B=68.3%×68.3%=46.6%: ±201、±202PB2=95.4%×95.4%=91.0%: ±301、±302:P=997%×99.7%=99.5% 航海上通常以三倍标准误差四边形为极限误差四边形 容易证明,标准误差四边形的面积为: 4o102 5,2sm0 其中0为1、两线的交角,O1、O,为两线的标准差。 因为船位落入标准误差四边形内的概率为定值(46.6%),所以标准误差四边形面积越 136
136 I 标准误差四边形 II I II 1P = 46.6% 2P = 91.1%3P = 95.5% 二倍标准误差四边形 三倍标准误差四边形 图 6.3.1 图 6.3.2 超出三倍标准误差带的概率为 0.3% ,几乎不可能出现. 因此,航海上常采用 95% 作 为船位误差界. 真实船位相对于最概率船位分布的误差界可用三种几何图形来描述,它们分 别是船位误差四边形、船位误差椭圆和船位误差圆. (1) 船位误差四边形 设Ⅰ、Ⅱ是两条同时观测到的船位线,其交点 p 是最或是船位. 若Ⅰ、Ⅱ分别存在的 标准差为 1、 2 ,则以 1 、 2 分别所作船位线Ⅰ、Ⅱ的平行线交成的四边形 ABCD 称为船位误差四边形(如图 6.3.2). 由它们的一倍、两倍、三倍标准误差带各自交成的平行四边形分别称为标准误差四边形、 二倍标准误差四边形、三倍标准误差四边形. 根据概率的乘法公式,可得船位落入标准误差 四边形内的概率分别为: 1、 2 : 1 p 0 0 0 = = 68.3 68.3 46.6 0 0 0 ; 21、 2 2 : 0 0 0 0 0 0 p2 = 95.4 95.4 = 91.0 ; 3 1、 3 2 : 0 0 0 0 0 0 p3 = 99.7 99.7 = 99.5 . 航海上通常以三倍标准误差四边形为极限误差四边形. 容易证明,标准误差四边形的面积为: sin 4 1 2 S1 = , 其中 为 I、II 两线的交角, 1、 2 为两线的标准差. 因为船位落入标准误差四边形内的概率为定值( 0 46.6 0 ),所以标准误差四边形面积越 +3 +2 + −3 −2 −

小,说明船位精度越高。其方法有:(1)减小σ,、σ,的值:(2)两线的交角越接近90越 好 6.3.2船位误差椭圆 由船位误差理论 N() 可知,船位落入最或 是船位处的概率最 0 大,而落入其它点的 概率密度,将随与最 或是船位点的距离的 B.a,Y 增大而减小。在标准 图6.3.3 差四边形周界内,将 真实船位出现的概率相等的各点连接起来,将是一个椭圆。由船位线标准差求得的椭圆,称 为船位标准误差椭圆.该椭圆内切于误差四边形,且切点为各边中点 设1、Ⅱ为两条独立的船位线,其标准误差分别为,02,两条船位线交角为0,两 位置线的交点是最或是船位.建立如图6.3.3所示的斜坐标系XOY,取I线为X轴,IⅡ 线为Y轴,观测船位点为原点.假定真船位于N点,I线的误差为4,IⅡ线的误差为D 于是真船位N的坐标位(x,y)为: Y=_D 可以推出,船位标准误差椭圆的方程为: 2 (ca)(cb=1 (6.3.1) 其中a=,b= sno sin o 当c=1时:称为一倍标准误差椭圆,船位落入的概率为:39.4%: 当c=2时:称为二倍标准误差椭圆,船位落入的概率为:86.5%: 当c=3时:称为三倍标准误差椭圆,船位落入的概率为:98.9%: 37
137 小,说明船位精度越高. 其方法有:(1)减小 1、 2 的值;(2)两线的交角越接近 0 90 越 好. 6.3.2 船位误差椭圆 由船位误差理论 可知,船位落入最或 是船位处的概率最 大,而落入其它点的 概率密度,将随与最 或是船位点的距离的 增大而减小. 在标准 差四边形周界内,将 真实船位出现的概率相等的各点连接起来,将是一个椭圆. 由船位线标准差求得的椭圆,称 为船位标准误差椭圆.该椭圆内切于误差四边形,且切点为各边中点. 设 I、II 为两条独立的船位线,其标准误差分别为 1 2 , ,两条船位线交角为 ,两 位置线的交点是最或是船位. 建立如图 6.3.3 所示的斜坐标系 XOY ,取 I 线为 X 轴,II 线为 Y 轴,观测船位点为原点. 假定真船位于 N 点,I 线的误差为 ,II 线的误差为 , 于是真船位 N 的坐标位( x y, )为: , . sin sin x y = = 可以推出,船位标准误差椭圆的方程为: 1 ( ) ( ) 2 2 2 2 + = cb y ca x (6.3.1) 其中 sin 2 a = , sin 1 b = . 当 c =1 时:称为一倍标准误差椭圆,船位落入的概率为: 0 39.4 0 ; 当 c = 2 时:称为二倍标准误差椭圆,船位落入的概率为: 0 86.5 0 ; 当 c = 3 时:称为三倍标准误差椭圆,船位落入的概率为: 0 98.9 0 ; III II I X Y O N x y ( , ) v 2 2 P , y x 图 6.3.3