
初等丞函数微分法 求导数的方法称为微分法。用定义只能求出 一 些较简单的函数的导数(常函数、幂函数、 正、余弦函数、指数函数、对数函数),对于 比较复杂的函数则往往很困难。本节我们就来 建立求导数的基本公式和基本法则,借助于这 些公式和法则就能比较方便地求出常见的函 数—初等函数的导数,从而是初等函数的求 导问题系统化,简单化
初等函数微分法 求导数的方法称为微分法。用定义只能求出 一些较简单的函数的导数(常函数、幂函数、 正、余弦函数、指数函数、对数函数),对于 比较复杂的函数则往往很困难。本节我们就来 建立求导数的基本公式和基本法则,借助于这 些公式和法则就能比较方便地求出常见的函 数——初等函数的导数,从而是初等函数的求 导问题系统化,简单化

一、和、差、积、商的求导法则 定理如果函数(x),v(x)在点x处可导,则它 们的和、差、积、商(分母不为零)在点x处也 可导,并且 (I)[u(x)士v(x)'=W'(x)±v'(x) (2)[u(x)v(x)]'=W'(x)y(x)+u(x)p'(x) 3r-tor四 (y(x)≠0), v2(x)
一、和、差、积、商的求导法则 定理 可导 并且 们的和、差、积、商 分母不为零 在点 处也 如果函数 在点 处可导 则它 , ( ) ( ), ( ) , x u x v x x ( ( ) 0). ( ) ( ) ( ) ( ) ( ) ] ( ) ( ) (3)[ (2)[ ( ) ( )] ( ) ( ) ( ) ( ); (1)[ ( ) ( )] ( ) ( ); 2 − = = + = v x v x u x v x u x v x v x u x u x v x u x v x u x v x u x v x u x v x
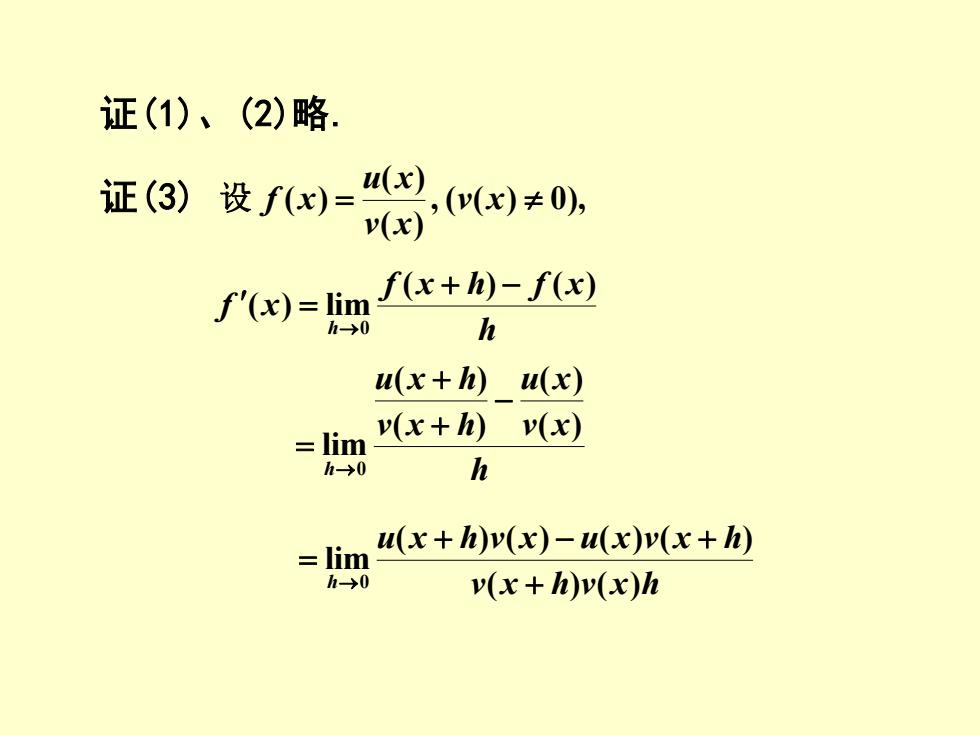
证(1)、(2)略. 证(3) 设f(x)= u(x ,(v(x)≠0), v(x) f'(x)=lim f(x+h)-f(x) h>0 h u(x+h)u(x) v(x+) lim v(x) h-→0 h u(x+h)v(x)-u(x)v(x+h) lim h-→0 v(x+h)v(x)h
证(1)、(2)略. 证(3) , ( ( ) 0), ( ) ( ) ( ) = v x v x u x 设 f x h f x h f x f x h ( ) ( ) ( ) lim 0 + − = → h v x u x v x h u x h h ( ) ( ) ( ) ( ) lim 0 − + + = → v x h v x h u x h v x u x v x h h ( ) ( ) ( ) ( ) ( ) ( ) lim 0 + + − + = →

=lim((-u(x)v-v(x)] h10 v(x+h)v(x)h u(x+h)-u(x) )-.x+)=w lim h h h→0 v(x+h)v(x) ='(x)p()-u4(x)p'(x) [w(x川2 f(x)在x处可导
v x h v x h u x h u x v x u x v x h v x h ( ) ( ) [ ( ) ( )] ( ) ( )[ ( ) ( )] lim 0 + + − − + − = → ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) lim 0 v x h v x h v x h v x v x u x h u x h u x h + + − − + − = → 2 [ ( )] ( ) ( ) ( ) ( ) v x u x v x − u x v x = f (x)在x处可导

注 ① (1)即是和、差的导数等于导数的和、差 (2)即是乘积的导数等于第一个因子的导数 乘以第二个因子再加上第一个因子乘以 第二个因子的导数 (3)即是商的导数等于分子的导数乘以分母 减去分子乘以分母的导数,再除以分母 的平方 ② (1)可推广到任意有限个可导函数的情形 fx=fx片 ③ (2)也可推广到任意有限个函数的情形
注 ① (1)即是和、差的导数等于导数的和、差 (2)即是乘积的导数等于第一个因子的导数 乘以第二个因子再加上第一个因子乘以 第二个因子的导数 (3)即是商的导数等于分子的导数乘以分母 减去分子乘以分母的导数,再除以分母 的平方 ② (1)可推广到任意有限个可导函数的情形 [ ( )] ( ); 1 1 = = = n i i n i fi x f x ③ (2)也可推广到任意有限个函数的情形

(uvw)'u'vw uv'w+uvw →fx川=xf(x).fn(x) +.+f(x)f2(x).f(x) =∑Πfx)f(x)为 i=1 k=1 k≠i 作为(2)的特殊情况 若v=c,则(cu'=cW或[Cf(x)'=Cf'(x); 即常数因子可以提到导数符号的外面 fr-2)
(uvw) = uvw + uvw + uvw ( ) ( ); ( ) ( ) ( ) [ ( )] ( ) ( ) ( ) 1 1 1 2 1 2 1 = = = = + + = n i n k i k i k n n n i i f x f x f x f x f x f x f x f x f x ④ 作为(2)的特殊情况 若v = c,则(cu) = cu 或 [Cf (x)] = Cf (x); 即常数因子可以提到导数符号的外面 [ ( )] ( ) 1 1 k f x k f x n i i i i n i i = = =

即线性组合的导数等于导数的线性组合 —说明求导是一线性运算 ⑤作为(3)的一种特殊情况, 若=1则中= 二、例题分析 例1求y=x3-2.x2+sinx的导数. 解 y'=3x2-4x+c0sx
即线性组合的导数等于导数的线性组合 ——说明求导是一线性运算 ⑤作为(3)的一种特殊情况, 2 ) 1 1, ( v v v u 若 = 则 = − 二、例题分析 例1 2 sin . 求 y = x 3 − x 2 + x的导数 解 2 y = 3x − 4x + cos x

例2求y=sin2xlnx的导数. 解 .y =2sinx.cosx.Inx y'=2c0sx·cosx·lnx+2sinx·(-sinx)·lnx +2sinx·cosx· x 1 =2cos 2x Inx+sin 2x. X 例3求y=tanx的导数. 解y=a=(0空
例 2 求 y = sin 2x ln x的导数 . 解 y = 2sin x cos x ln x y = 2cos x cos x ln x + 2sin x (− sin x) ln x x x x 1 + 2sin cos sin 2 . 1 2cos 2 ln x x = x x + 例 3 求 y = tan x的导数 . 解 ) cos sin = (tan ) = ( xx y x
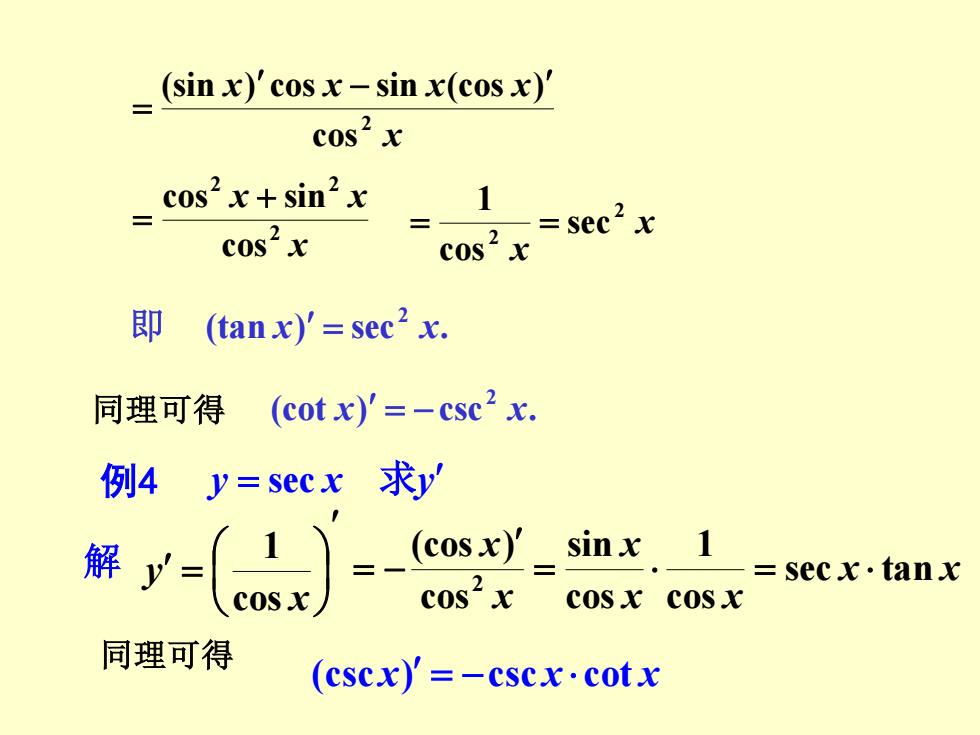
(sin x)'cosx-sin x(cosx)' cos2 x cos'x+sin'x cos2x -=sec2x cos 即 (tanx)'=sec2 x. 同理可得(C0tx)'=-csc2x. 例4y=secx求y' 部r-(e=-oa cos2x cosx cosx 同理可得 (cscx)'=-cscx·cotx
x x x x x 2 cos (sin ) cos − sin (cos ) = x x x 2 2 2 cos cos + sin = x x 2 2 sec cos 1 = = (tan ) sec . 2 即 x = x 同理可得 (cot ) csc . 2 x = − x 例4 y = sec x 求y 解 = x y cos 1 x x 2 cos (cos ) = − x x x x x sec tan cos 1 cos sin = = 同理可得 (cscx) = −csc x cot x
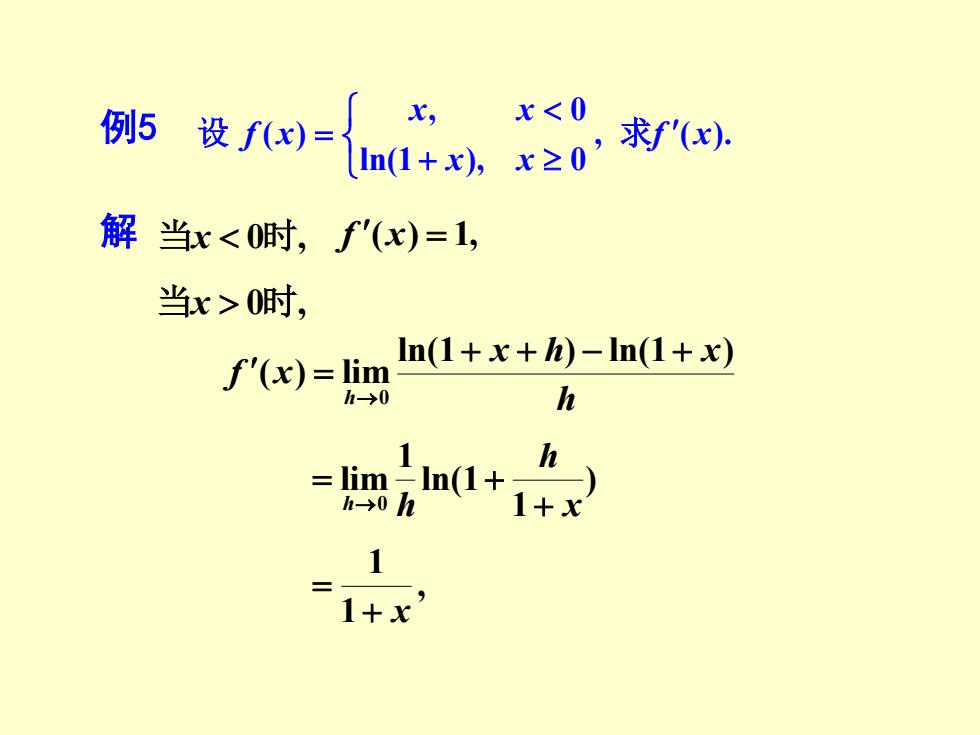
s设-{0n 解当x0时, ln(1+x+-ln(1+x) f(x)=lim →0 h 1+x
例 5 , ( ). ln(1 ), 0 , 0 ( ) f x x x x x f x + 设 = 求 解 当 x 0 时 , f ( x ) = 1 , 当 x 0 时 , h x h x f x h ln(1 ) ln(1 ) ( ) lim0 + + − + = → ) 1 ln( 1 1 lim0 x h h h + = + → , 1 1+ x =