
定积分的性质 一、基本内容 对定积分的补充规定: (1)当a=b时,∫f(x)dc=0: (2)当a>b时,f(x)k=-f(x)d. 说明在下面的性质中,假定定积分都存 在,且不考虑积分上下限的大小
对定积分的补充规定: (1)当a = b时, ( ) = 0 b a f x dx ; (2)当a b时, = − a b b a f (x)dx f (x)dx. 在下面的性质中,假定定积分都存 在,且不考虑积分上下限的大小. 说明 定积分的性质 一、基本内容

性质1 ∫fx)±g(x)=∫f(x)c±∫g(x)d. 证f(x)±g(x)=lim∑Lf(5)±g(5:)l△x 九-→0 i=1 =lim∑f(5)△x,±im∑g(5,)Ac, 0 九→0 i=1 =∫f(x)±g(x)k. (此性质可以推广到有限多个函数作和的情况) j2em-2jfxa
b a [ f (x) g(x)]dx= b a f (x)dx b a g(x)dx . 证 b a [ f (x) g(x)]dx i i i n i = f g x = → lim [ ( ) ( )] 1 0 i i n i = f x = → lim ( ) 1 0 i i n i g x = → lim ( ) 1 0 = b a f (x)dx ( ) . b a g x dx (此性质可以推广到有限多个函数作和的情况) 性质1 = = = b a n i b a i n i f i x dx f x dx 1 1 [ ( )] ( )

性质2 ∫f(x)d&=kfx) (k为常数), 证 kf(x)dk=lim∑f(传)△x, 元0=1 =mk空f5A,=km2f传,)Ax 九-→0 i=1 -k["f(x)dx. 性质1+性质2 得:
性质2 = b a b a kf (x)dx k f (x)dx (k为常数). 证 b a kf (x)dx i i n i = kf x = → lim ( ) 1 0 i i n i = k f x = → lim ( ) 1 0 i i n i = k f x = → lim ( ) 1 0 ( ) . = b a k f x dx 性质1+性质2 得:

[I()+ig(xdx -2对ee+etea 推广: fxds b a i=l i= 即线性组合的定积分等于定积分的线性组合 说明定积分也具有线性运算性质
+ b a [f (x) g(x)]dx = + b a b a f (x)dx g(x)dx 推广: = = = b a n i n i b a ki f i x dx ki f i x dx 1 1 [ ( )] ( ) 即线性组合的定积分等于定积分的线性组合 ——说明定积分也具有线性运算性质

性质3 假设a<c<b )=+d. 补充:不论α,b,c的相对位置如何,上式总成立 例若a<b<c, (df()(d 则f)k=f)-fxw)d -[f(x)dx+"f(x)dx. (定积分对于积分区间具有可加性)
假设a c b b a f (x)dx = + b c c a f (x)dx f (x)dx. 补充:不论 a,b,c 的相对位置如何, 上式总成立. 例 若 a b c, c a f (x)dx = + c b b a f (x)dx f (x)dx b a 则 f (x)dx = − c b c a f (x)dx f (x)dx ( ) ( ) . = + b c c a f x dx f x dx (定积分对于积分区间具有可加性) 性质3

性质4∫1k=k=b-a. 性质5(非负性)如果在区间4,b]上f(x)≥0, 则f(x)&≥0.(a<b) 证f(x)≥0,.f(传)≥0,(i=1,2,.,n) △x≥0,.∑f(传)A,≥0, 2=max{△x1,△x2,.,△xn} im2f5ax=fed≥0
dx b a 1 dx b a = = b − a. 性质5(非负性) 如果在区间[a,b]上 f (x) 0, 则 ( ) 0 f x dx b a . (a b) 证 f (x) 0, ( ) 0, i f (i = 1,2, ,n) 0, xi ( ) 0, 1 = i i n i f x max{ , , , } = x1 x2 xn i i n i f x = → lim ( ) 1 0 ( ) 0. = b a f x dx 性质4

例1比较积分值厂ek和xk的大小. 解令f(x)=e'-x, x∈[-2,0] f(x)>0,.,(e*-x)c>0, ,e*>∫k,于是e*k<. 性质5的推论:(比较定理) (1) 如果在区间a,b]上f(x)≤g(x), 则f(x)k≤∫g(x). (a<b) (2)f(x)≤f(x)k.(a<b) 说明:f(x)川在区间[M,b]上的可积性是显然的
例 1 比较积分值 e dx x −2 0 和 xdx −2 0 的大小. f (x) e x, x 令 = − x[−2, 0] f (x) 0, ( ) 0, 0 2 − − e x dx x e dx x − 0 2 , 0 2 xdx − 于是 e dx x −2 0 . 2 0 xdx − 性质5的推论:(比较定理) 则 f x dx b a ( ) g x dx b a ( ) . (a b) (1) 如果在区间[a,b]上 f (x) g(x), (2) f x dx b a ( ) f x dx b a ( ) . (a b) 说明:| f (x)|在区间[a,b]上的可积性是显然的. 解

性质6(估值定理)设M及m分别是函数 f(x)在区间[a,b]上的最大值及最小值, 则m(b-a)≤∫f(x≤M(b-). Em≤f()sM,.m≤f(x)dc≤iM m(b-a)≤f(x)k≤Mb-a). (此性质可用于估计积分值的大致范围) 2估计积分∫血在的值 解 f(x)=si
设M及m分别是函数 f (x)在区间[a,b]上的最大值及最小值, 则 m(b a) f (x)dx M(b a) b a − − . 证 m f (x) M, ( ) , b a b a b a mdx f x dx Mdx m(b a) f (x)dx M(b a). b a − − (此性质可用于估计积分值的大致范围) 例 2 估计积分 dx x x 2 4 sin 的值. 解 , sin ( ) x x f x = ] 2 , 4 [ x 性质6(估值定理)
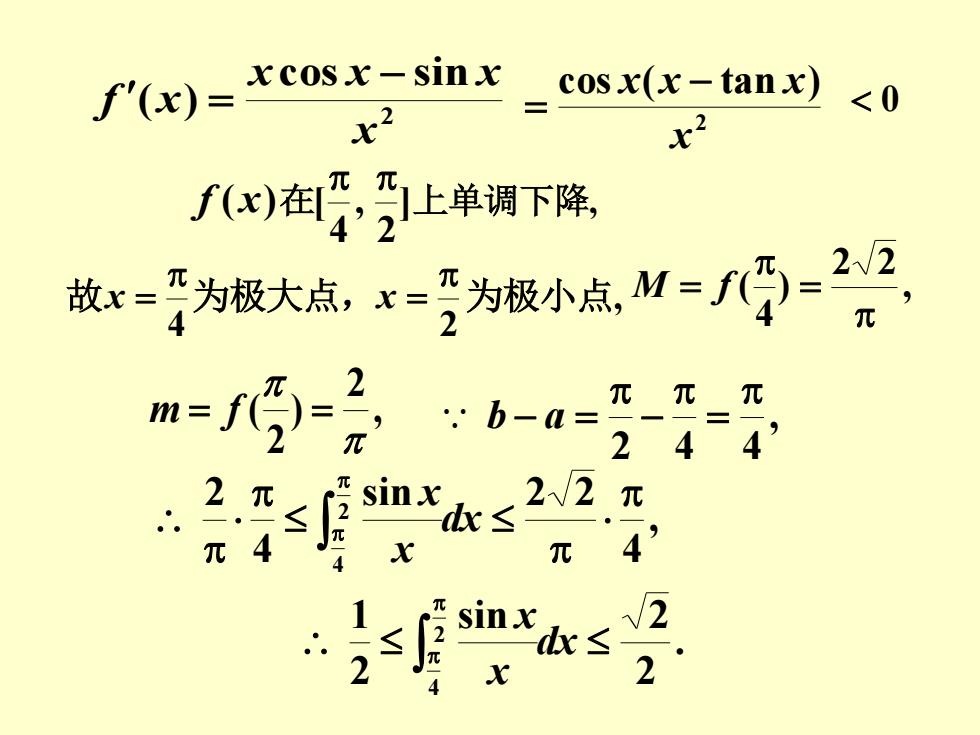
f'(x)= xcosx-sinx cosx(x-tanx) <0 x2 x2 x)在亚上单调下降 故x-为极大点,x=为极小点M=骨=22, m=⑨:-a 兀兀元 2447 ssinx 2√2元 ~d≤ 元4 π4 、≤2 2 ≤ 2
2 cos sin ( ) x x x x f x − = 2 cos ( tan ) x x x − x = f (x)在 ] 2 , 4 [ 上单调下降, 故 4 x = 为极大点, 2 x = 为极小点, , 2 2 ) 4 ( = M = f , 2 ) 2 ( m = f = , 2 4 4 = − b − a = , 4 sin 2 2 4 2 2 4 dx x x . 2 sin 2 2 1 2 4 dx x x 0

性质7(定积分中值定理) 如果函数f(x)在闭区间[α,b]上连续, 则在积分区间4,b]上至少存在一个点5, 使f(x)=f(传)(b-).(a≤专≤b) 积分中值公式 证 'm(b-a)≤f(x)c≤M(b-a) :m≤6afwh≤M 由闭区间上连续函数的介值定理知
如果函数 f (x)在闭区间[a,b]上连续, 则在积分区间[a,b]上至少存在一个点 , 使 f x dx b a ( ) = f ( )(b − a). (a b) 积分中值公式 证 m(b a) f (x)dx M(b a) b a − − f x dx M b a m b a − ( ) 1 由闭区间上连续函数的介值定理知 性质7(定积分中值定理)