
定积分的分都积分法 一、分部积分公式 定积分也可以象不定积分一样进行分部积分, 设函数u(x)、v(x)在区间a,b]上具有连续导数,则 有dw=[uv时-da. 定积分的分部积分公式 推导(ar=y+以,心ay=u可, [uvl=∫t'c+∫uv'idk, i.fudv=[avvda
定积分也可以象不定积分一样进行分部积分, 设函数u(x)、v( x)在区间a,b上具有连续导数,则 有 = − b a b a b a udv uv vdu. 定积分的分部积分公式 推导 (uv) = uv + uv , ( ) , b a b a uv dx uv = , = + b a b a b a uv u vdx uv dx . = − b a b a b a udv uv vdu 定积分的分部积分法 一、分部积分公式

例1计算 ∫aresin xx. 解令u=arcsin七,dy=d, 则du= V1-x2,v=, fareins arcn 君+就-)
解 arcsin . 2 1 0 xdx 令 u = arcsin x, dv = dx, 则 , 1 2 x dx du − = v = x, 2 1 0 arcsin xdx 2 1 = xarcsin x 0 − − 2 1 0 2 1 x xdx 2 6 1 = (1 ) 1 1 2 1 2 0 2 2 1 d x x − − + 12 = 2 1 0 2 + 1− x 1. 2 3 12 = + − 例1 计算
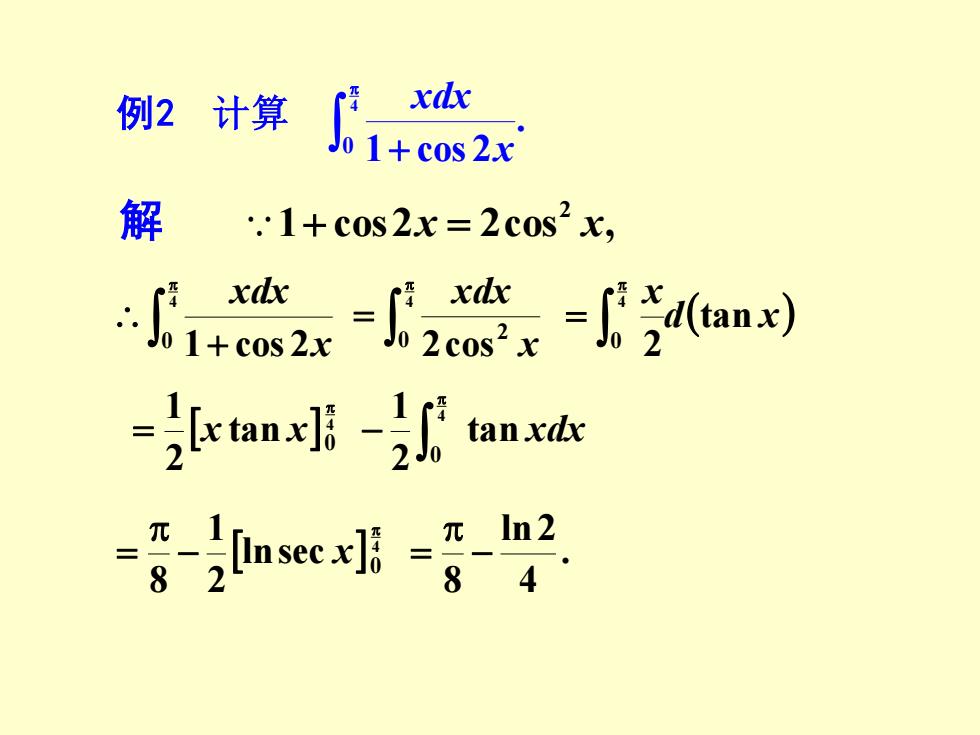
例2计算 1+w2 x 解 1+c0s2x=2c0s2K, -+流=流-a划 =cany月-an 5恤sc时明-g-2
1 cos2 2cos , 2 + x = x + 4 0 1 cos 2x xdx = 4 0 2 2cos x xdx d( x) x tan 2 4 0 = 4 0 tan 2 1 = x x tan xdx 2 1 4 0 − 4 0 lnsec 2 1 8 − = x . 4 ln2 8 − = 例2 计算 . 1 cos 2 4 0 + x xdx 解

例3计算 解 x=-1*3+ =-[n"+]+2+n1+刘 In2 +2 1 1 1+x2+x =-n2+n(1+x)-lm(2+xj = 3 5n2-ln3
例3 计算 . (2 ) 1 ln(1 ) 0 2 + + dx x x 解 + 1 + 0 2 (2 ) ln(1 ) dx x x + = − + 1 0 2 1 ln(1 ) x x d 1 2 0 ln(1 ) + + = − x x + + + 1 0 ln(1 ) 2 1 d x x 3 ln2 = − dx x x + + + 1 0 1 1 2 1 x + x − + 2 1 1 1 1 0 ln(1 ) ln(2 ) 3 ln2 = − + + x − + x ln2 ln3. 3 5 = −

4设fx)=in,求k、 解因为sin没有初等形式的原函数, 无法直接求出f(x),所以采用分部积分法 (dx) =2rf- =f四-2fww
例 4 设 = 求 2 1 , sin ( ) x dt t t f x ( ) . 1 0 xf x dx 解 因为 t sint没有初等形式的原函数, 无法直接求出 f (x),所以采用分部积分法 10 xf ( x )dx = 10 2 ( ) ( ) 21 f x d x 10 2 ( ) 21 = x f x − 10 2 ( ) 21 x df x ( 1 ) 21 = f − 10 2 ( ) 21 x f x dx
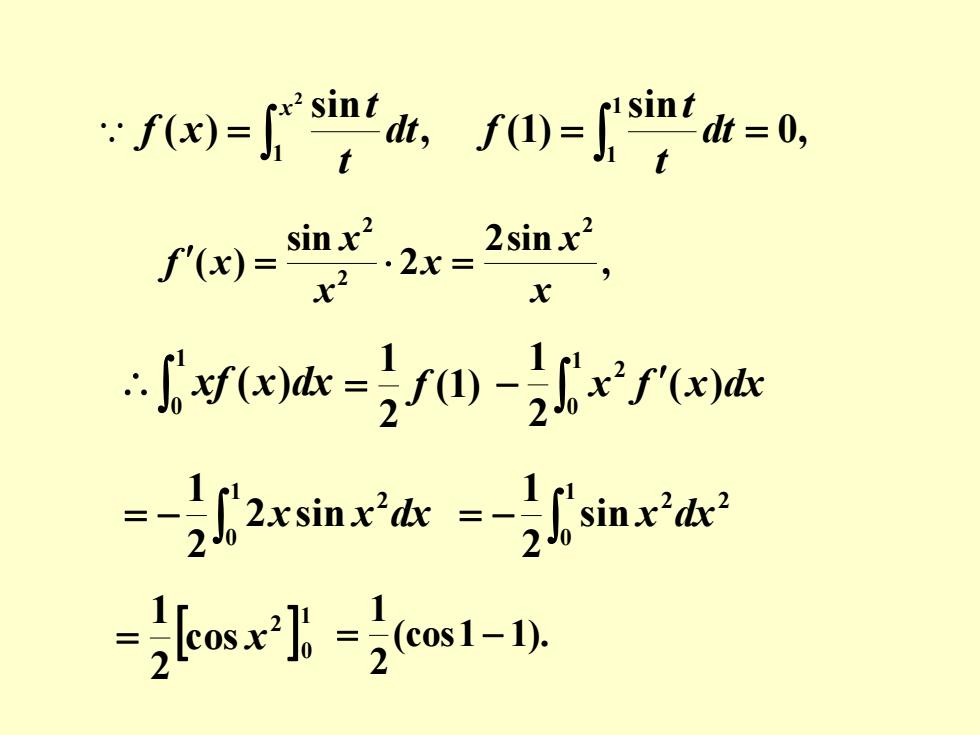
)sint d.m 22 f')= in x2 ÷e=20-2xfww xsin'ids sinxids -eos(ns1-1)
0, sin (1) 1 1 = dt = t t f = 2 1 , sin ( ) x dt t t f x , 2sin 2 sin ( ) 2 2 2 x x x x x f x = = 1 0 xf (x)dx (1) 2 1 = f − 1 0 2 ( ) 2 1 x f x dx = − 1 0 2 2 sin 2 1 x x dx = − 1 0 2 2 sin 2 1 x dx 1 0 2 cos 2 1 = x (cos1 1). 2 1 = −

例5证明定积分公式 Isin"xdfcos"xd n-1n-3 31π n n-2 422 n为正偶数 n-1n-3 42 为大于1的正奇数 、nn-253 证设u=sin"-lx,dw=sinxdx, du =(n-1)sin"xcosxdx,v=-cosx, sim(1sin 0 1-sin-x
= = 2 2 0 0 I sin xdx cos xdx n n n − − − − − − = n n n n n n n n n n , 3 2 5 4 2 1 3 , 2 2 1 4 3 2 1 3 为正偶数 为大于1的正奇数 证 设 sin , 1 u x n− = dv = sin xdx, ( 1)sin cos , 2 du n x xdx n− = − v = −cos x, I x x n x xdx n n n − − = − + − 2 2 0 2 2 0 1 sin cos ( 1) sin cos 0 x 2 1− sin 例5 证明定积分公式

=(n-1)sin-2 xd-(n-1)f sin"xd =(n-1)lm-2-(n-1)Im 积分I关于下标的递推公式 1n-2= n-3 ,直到下标减到0或1为止 n-2 n-4 12m 2m-1.2m-3.5.31n, 2m2m-2 642 2m2m-2642 (m=1,2, L2m+1 2m+12m-1.75‘3, ●
I n xdx n xdx n n n = − − − 2 − 2 0 0 2 ( 1) sin ( 1) sin n n (n 1)I (n 1)I = − −2 − − 2 1 − − n = n I n n I 积分 In 关于下标的递推公式 2 4 2 3 − − − − n = n I n n I , 直到下标减到0或1为止 , 2 1 4 3 6 5 2 2 2 3 2 2 1 2 0 I m m m m I m − − − = (m = 1,2, ) , 3 2 5 4 7 6 2 1 2 2 2 1 2 2 1 1 I m m m m I m − − + + =
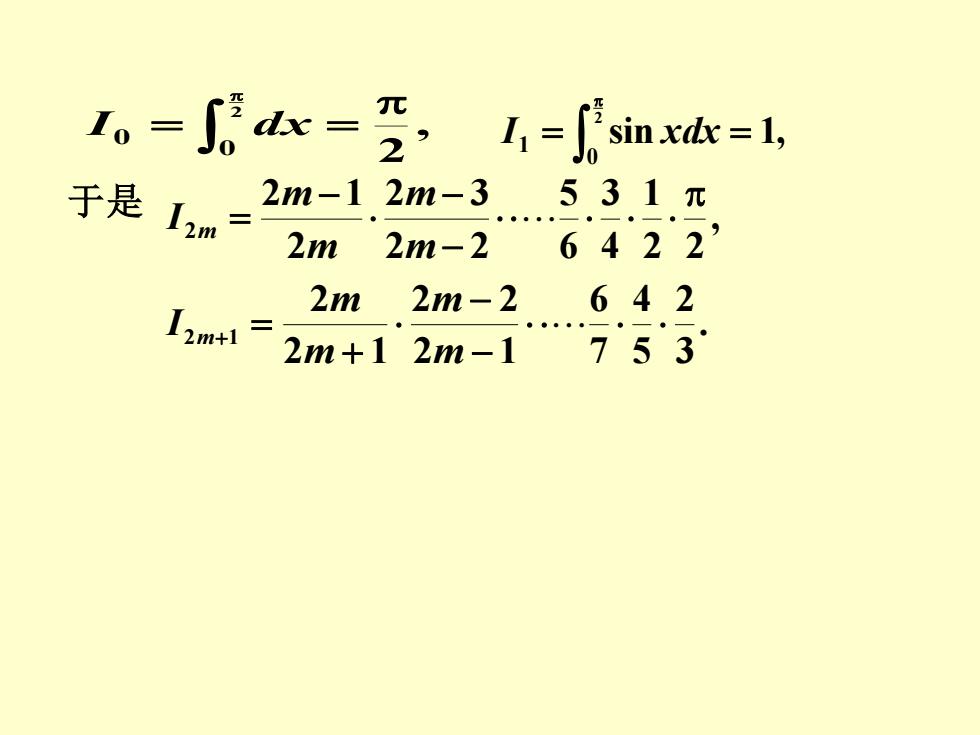
。=Jc=空,五=jsi流=1 0 于是 1n=2m-1.2m-3531元 2m2m-26422' L2m+1 2m2m-2642 2m+12m-1753
, 2 2 0 0 = = I dx sin 1, 2 0 1 = = I xdx 于是 , 2 2 1 4 3 6 5 2 2 2 3 2 2 1 2 − − − = m m m m I m . 3 2 5 4 7 6 2 1 2 2 2 1 2 2 1 − − + + = m m m m I m

例6设f(x)连续证明 jc-n0a=对0o咖w 证一记F(x)=j(x-t)f()h cuw-io咖r 则 F'(x)=G'(x)=∫f(t)dt→F(x)-G(x)=C 0 而F(O)=G(0)=0故F(x)=G(x)
设 f ( x ) 连续 证明 x t f t dt f u du dt x x t − = 0 0 0 ( ) ( ) ( ) 证一记 = − x F x x t f t dt 0 ( ) ( ) ( ) G x f u du dt x t = 0 0 ( ) ( ) 则 = = x F x G x f t dt 0 ( ) ( ) ( ) F(x) − G(x) = C 而 F(0) = G(0) = 0 故 F(x) = G(x) 例6