
第四章不定积分 教学目的: 1.理解原函数与不定积分的概念,掌握不定积分的性质: 2.熟练使用不定积分的基本公式: 3。掌握直接积分法,换元积分法和分部积分法。 4.1不定积分的概念与性质 4.1.1不定积分的概念 【讲解】原函数的概念 定义1设f(x)是定义在某区间I上的已知函数,如果有函数F(x)满 足:F(x)=f(x)或dF(x)=f(x),则称F(x)是f(x)在该区间1 上的一个原函数。 【板演】例1因为(sinx)=cosx,x∈(-o,+oo)所以 sinx是cosx在(-o,+oo)上的一个原函数。 【板演】例2因为(x)=5x4,(x3+2)=5x4,(x3-√7)=5x4, (x+C)=5x(C为任意常数) 所以x,,x+2,x-√7,x+C都是5x的原函数。 【结论】 1、一个函数的原函数若存在,则原函数不唯一,且有无穷多个。 2、同一函数的原函数之间只相差一个常数。 3、若F(x)为f(x)的一个原函数,则F(x)+C可表示f(x)的所有原 函数(C为任意常数)。 【讲解】不定积分的概念 定义2若函数F(x)是f(x)在区间I上的一个原函数,那么f(x)的 所有原函数F(x)+C(C为任意常数),称为f(x)在区间I上的不定 积分。记作「f(x)dk,即 1
1 第四章 不定积分 教学目的: 1. 理解原函数与不定积分的概念,掌握不定积分的性质; 2. 熟练使用不定积分的基本公式; 3. 掌握直接积分法,换元积分法和分部积分法。 4.1 不定积分的概念与性质 4.1.1 不定积分的概念 【讲解】原函数的概念 定义1 设 f (x) 是定义在某区间 I 上的已知函数,如果有函数 F(x) 满 足: F(x) = f (x)或dF(x) = f (x)dx,则称 F(x) 是 f (x) 在该区间 I 上的一个原函数。 【板演】例 1 因为 (sin x) cos x ' = , x (−,+) 所以 sin x 是 cos x 在 (−,+) 上的一个原函数。 【板演】例 2 因为 5 ' 4 (x ) = 5x , 5 ' 4 (x + 2) = 5x , 5 ' 4 (x − 7) = 5x , 5 ' 4 (x +C) = 5x ( C 为任意常数) 所以 5 x , 2 5 x + , 7 5 x − , x + C 5 都是 4 5x 的原函数。 【结论】 1、 一个函数的原函数若存在,则原函数不唯一,且有无穷多个。 2、 同一函数的原函数之间只相差一个常数。 3、若 F(x) 为 f (x) 的一个原函数,则 F(x) + C 可表示 f (x) 的所有原 函数( C 为任意常数)。 【讲解】不定积分的概念 定义 2 若函数 F(x) 是 f (x) 在区间 I 上的一个原函数,那么 f (x) 的 所有原函数 F(x) + C ( C 为任意常数),称为 f (x) 在区间 I 上的不定 积分。记作 f (x)dx ,即
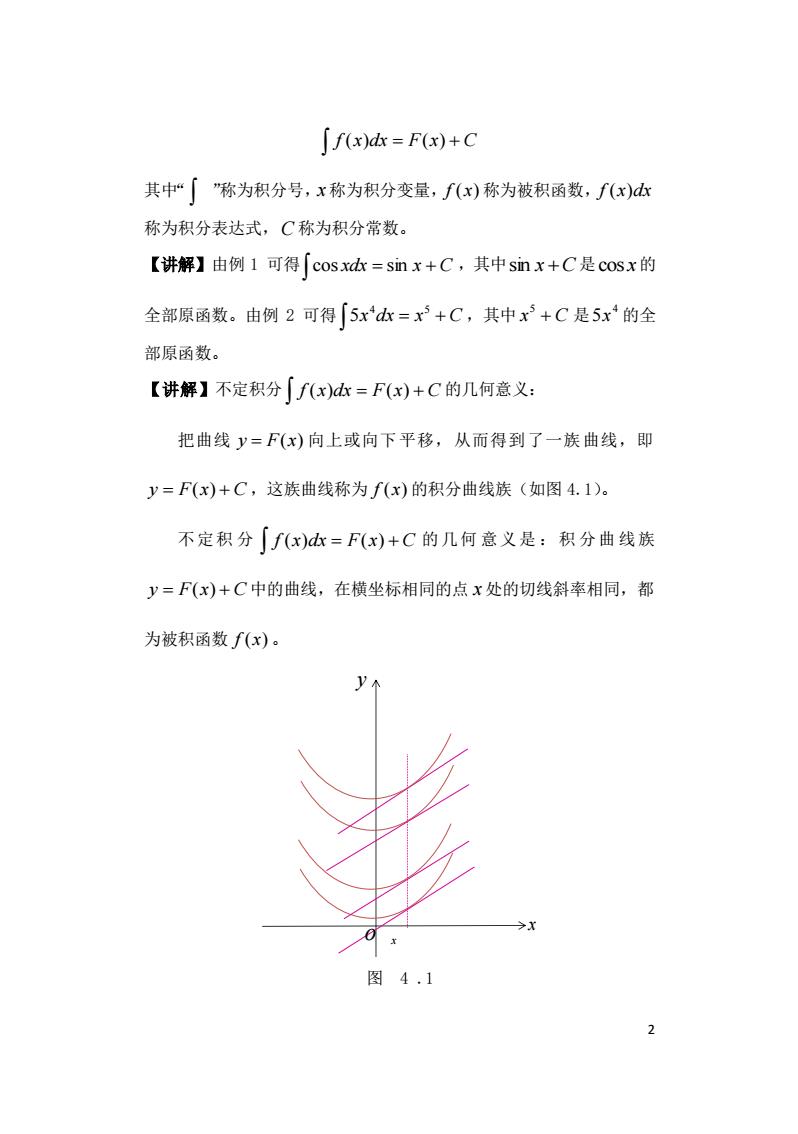
[f(x)dx=F(x)+C 其中“了」"称为积分号,x称为积分变量,f(x)称为被积函数,f(x)d 称为积分表达式,C称为积分常数。 【讲解】由例1可得[cosxdx=snx+C,其中snx+C是cosx的 全部原函数。由例2可得[5xd=x3+C,其中x+C是5x的全 部原函数。 【讲解】不定积分「f(x)dk=F(x)+C的几何意义: 把曲线y=F(x)向上或向下平移,从而得到了一族曲线,即 y=F(x)+C,这族曲线称为f(x)的积分曲线族(如图4.1)。 不定积分f(x)dk=F(x)+C的几何意义是:积分曲线族 y=F(x)+C中的曲线,在横坐标相同的点x处的切线斜率相同,都 为被积函数f(x)
2 f (x)dx = F(x) + C 其中“ ”称为积分号, x 称为积分变量, f (x) 称为被积函数, f (x)dx 称为积分表达式, C 称为积分常数。 【讲解】由例 1 可得 xdx = x + C cos sin ,其中 sin x +C 是 cos x 的 全部原函数。由例 2 可得 x dx = x + C 4 5 5 ,其中 x + C 5 是 4 5x 的全 部原函数。 【讲解】不定积分 f (x)dx = F(x) + C 的几何意义: 把曲线 y = F(x) 向上或向下平移,从而得到了一族曲线,即 y = F(x) + C ,这族曲线称为 f (x) 的积分曲线族(如图 4.1)。 不定积 分 f (x)dx = F(x) + C 的几何 意义是 :积 分曲 线族 y = F(x) + C 中的曲线,在横坐标相同的点 x 处的切线斜率相同,都 为被积函数 f (x) 。 x y o x 图 4 .1

4.1.2不定积分的性质(运算性质): 【讲解】性质1求不定积分与求导数或微分互为逆运算(互逆性)。 (1)不定积分的导数(或微分)等于被积函数(或被积表达式) f(x)dx]=f(x)d f(x)dx=f(x)dx 例如,因为(x2y=2x,有可2xd=2x,d2xdk=2xd (2)一个函数的导数(或微分)的不定积分与这个函数相差一个 任意常数。 F(x)dx F(x)+CdF(x)=F(x)+C 例如,因为(x3y=3x2,有「(x3)dk=x3+C,「3=x3+C 【讲解】性质2不为0的常数因子,可以移到积分号前(齐次性)。 「af(x)dk=a[f(x)dk(a为非零常数) 【讲解】性质3两个函数和差的不定积分,等于两个函数不定积分的 和差(可加性)。 ff(x)±g(xldt=「f(x)dk±[g(x)c 由性质2和性质3得: 【讲解】「[af(x)±bg(x)k=a[f(x)dk±bg(x)dk(a,b为非零 常数) 4.1.3不定积分的基本公式一一直接积分法 1、公式记忆 因为 积分公式 求导公式 1.「dk=x+C (1)x'=1 (C)y=0 ∫oak=c
3 4. 1. 2 不定积分的性质(运算性质): 【讲解】性质 1 求不定积分与求导数或微分互为逆运算(互逆性)。 (1)不定积分的导数(或微分)等于被积函数(或被积表达式) [ ( ) ] = ( ) ' f x dx f x 或 d f (x)dx = f (x)dx 例如,因为 (x ) 2x 2 = ,有 [ 2xdx] = 2x ' , d 2xdx = 2xdx (2)一个函数的导数(或微分)的不定积分与这个函数相差一个 任意常数。 F x dx = F x + C ( ) ( ) ' 或 dF x = F x + C ( ) ( ) 例如,因为 3 2 (x ) = 3x ,有 x dx = x + C 3 ' 3 ( ) , dx = x + C 3 3 【讲解】性质 2 不为 0 的常数因子,可以移到积分号前(齐次性)。 af (x)dx a f (x)dx (a为非零常数) = 【讲解】性质 3 两个函数和差的不定积分,等于两个函数不定积分的 和差(可加性)。 [ f (x) g(x)]dx = f (x)dx g(x)dx 由性质 2 和性质 3 得: 【讲解】 [af (x) bg(x)]dx = a f (x)dx b g(x)dx ( a,b 为非零 常数) 4.1.3 不定积分的基本公式——直接积分法 1、公式记忆 因为 积分公式 求导公式 1. dx = x + C , 0dx = C (1) x =1 (C) = 0

2.x“k=1 Γa+1 a1+C其中a是 (2)(x")=ax 常数,a≠-1 空-+C ) (log =-loge= 1 xlna 1 特别(hx'= x 4.「a'dk= 1a+C,其中a>0 (4)(a)'=ana,其中 且a≠1 a>0且a≠1 特别∫e'd=e'+C 5. 「cosxdx=sinx+C (5)(sin x)=cosx 6. [sin xdx=-cosx+C (6)(cosx)'=-sin x (7)(tanx)'=sec2x (8)(cotx)'=-csc2x l盘-je-omr+C 9 =arcsin x+C 1 (arcsin x)'=- 1-x2 10 10. arctan x+C 1 (arctan x)'= 1+x2 4
4 2. x dx x + C + = + 1 1 1 其中 是 常数, −1 (2) 1 ( ) − = a a x ax 3. x C x dx = + ln ( 3 ) x a e x x a a ln 1 log 1 (log ) = = 特别 x x 1 (ln ) = 4. a C a a dx x x = + ln 1 ,其中 a 0 且 a 1 特别 e dx e C x x = + (4) a a a x x ( ) = ln ,其中 a 0 且 a 1 5. cos xdx = sin x + C (5) (sin x) = cos x 6. sin xdx =-cos x + C (6) (cos x) = −sin x 7. xdx x C x dx = = + sec tan cos 2 2 (7) x x 2 (tan ) = sec 8 . xdx x C x dx = = − + csc cot sin 2 2 (8) x x 2 (cot ) = −csc 9. x C x dx = + − arcsin 1 2 ( 9 ) 2 1 1 (arcsin ) x x − = 10. x C x dx = + + arctan 1 2 ( 10 ) 2 1 1 (arctan ) x x + =

【板演】例1计算不定积分「xd 第∫4r=4+C=+C 【板演】例2计算不定积分「2k 」积分公式4 解j2rk=22r+C 【板演】例3计算不定积分「(3simx+√)d 「(3snx+√F) 性质3 =∫3snxd+东dk 性质2 =3 si xd+∫x2k 积分公式5、2 =-3cosx+C,+( 1+C:r =-+号G+G 注意等式右端的每个不定积分都有一个任意常数,有限个任意常数 的代数和还是一个任意常数,所以上式只写一个任意常数。 作业:习题4.1一1、2、3 4.2换元积分法 【引入】在不定积分的计算中大多数不定积分不能直接求出。例如: 计算不定积分∫cos3x和∫e2k及∫V1-x2dc等等。这是因为 被积函数都是复合函数,根据积分与微分的互逆关系,复合函数的求 导法则反过来也可用于求不定积分。利用中间变量的代换,可得到不 定积分的基本计算方法一一换元积分法。第一类换元积分法也叫凑微 5
5 【板演】例 1 计算不定积分 x dx 3 解 x dx x + C = x + C + = + 3 3 1 4 3 1 1 4 4 【板演】例 2 计算不定积分 dx x 2 解 dx C x x = + 2 ln 2 1 2 【板演】例 3 计算不定积分 (3sin x + x)dx 解 (3sin x + x)dx = 3sin xdx + xdx = xdx + x dx 2 1 3 sin = ) 1 2 1 1 3cos ( 2 1 2 1 x C1 x + C + − + + + = ( ) 3 2 3cos 1 2 2 3 − x + x + C + C = − x + x 2 + C 3 3 2 3cos 注意 等式右端的每个不定积分都有一个任意常数,有限个任意常数 的代数和还是一个任意常数,所以上式只写一个任意常数。 作业:习题 4.1—1、2、3 4.2 换元积分法 【引入】在不定积分的计算中大多数不定积分不能直接求出。例如: 计算不定积分 cos3xdx 和 e dx 2x 及 x dx − 2 1 等等。这是因为 被积函数都是复合函数,根据积分与微分的互逆关系,复合函数的求 导法则反过来也可用于求不定积分。利用中间变量的代换,可得到不 定积分的基本计算方法——换元积分法。第一类换元积分法也叫凑微 积分公式 4 性质 3 性质 2 积分公式 5、2

分法:第二类换元积分法也叫变量置换法。 4.2.1凑微分法 【板演】例1计算不定积分[cos3x 【分析】被积函数是复合函数c0s3x=cosu,而中间变量u=3x且 du=d(3x)=3dx。显然,被积表达式中缺少常数3,故可改变被积表达式 的系数凑出中间变量的微分,即cos3xdx=cos3x·3 dx=cos udu。 由4.1知: ∫os3h凑微分cos3x-3h著 du=3dx 3 r3t∫cosudu=3sinu+c 回代1 in3x+C M=3x3 【复演1例2计算不定积分∫,2小 【分析】技积函数是复合函数十2:7 1=1,而中间变量u=1+2x且 du=d(1+2x)=2dk。显然,应在被积表达式中改变系数凑出中间变 1 量的微分,即: 1+2x=21+2 ,凑微分1「12水 接元=a0ap+c 做+22本=d21+2r1+22 回代1 In1+2x+C u=1+2x2 【讲解】定理1 如果∫f(x)dk=F(x)+C则∫f()du=F(u)+C 6
6 分法;第二类换元积分法也叫变量置换法。 4.2.1 凑微分法 【板演】例 1 计算不定积分 cos3xdx 【分析】 被积函数是复合函数 cos3x=cosu,而中间变量 u=3x 且 du=d(3x)=3dx。显然,被积表达式中缺少常数 3,故可改变被积表达式 的系数凑出中间变量的微分,即 = 。 由 4.1 知: 1 1 1 cos 3 cos 3 3 cos sin 3 3 3 3 3 1 sin 3 3 3 xdx x dx udu u C du dx x u x C u x = + = = + = 凑微分 换元 回代 【板演】例 2 计算不定积分 1 1 2 dx + x 【分析】被积函数是复合函数 1 1 1 2x u = + ,而中间变量 u x = +1 2 且 du d x dx =+= (1 2 2 ) 。显然,应在被积表达式中改变系数凑出中间变 量的微分,即 1 1 1 1 1 2 1 2 2 1 2 2 dx dx du x x u = = + + ( ) 1 1 1 1 1 1 1 2 ln ln 1 2 2 1 2 2 2 2 2 1 2 1 ln 1 2 1 2 2 dx dx du d u u C x x u dx du x u x C u x = = + + + = + = + + = + 凑微分 换元 故 回代 【讲解】定理 1 f x dx F x C f u du F u C ( ) ( ) ( ) ( ) = + = + 如果 则

其中u=(x)是x的任意可微函数。 【板演】推论若f()du=F(u+C且u=(x)可微,则有 ∫f[(x)]p'(x)dk凑微分∫f[(x)]d(x) 换元 (x)=u f(u)du =x)+ 回代 F[(x)]+C .(1 u=(x) 上述(1)式通常也叫第一类换元积分公式。 【讲解】这种先将不定积分被积表达式中分解出的'(x)d山凑成微分 d(x),再作变量代换(x)=u,将原不定积分转化为利用基本积分 公式容易计算的积分「f():,这种方法就叫凑微分法,也叫第一类 换元积分法。 【讲解】注意由定理1可知:将基本积分公式中的积分变量换成任 意一个可微函数,公式仍成立。例如将「cosxdx=sinx+C中积分变 量x换做可微函数3+5x2,则有 「cos(3+5x2)d(3+5x2)=sin(3+5x2)+C 【学生板演】例3计算不定积分「(3x+8)'d 7
7 其中u x x =( )是 的任意可微函数。 【板演】 推论 若 f u du F u C ( ) ( ) = + 且 u x = ( ) 可微,则有 ( ) ( ) ( ) ( ) ( ) ( ) ( ) [ ( )] (1) ( ) f x x dx f x d x f u du x u F x C F x C u x = = + + = 凑微分 换元 回代 上述(1)式通常也叫第一类换元积分公式。 【讲解】这种先将不定积分被积表达式中分解出的 ( ) x dx 凑成微分 d x ( ) ,再作变量代换 ( ) x u = ,将原不定积分转化为利用基本积分 公式容易计算的积分 f u du ( ) ,这种方法就叫凑微分法,也叫第一类 换元积分法。 【讲解】注意 由定理 1 可知:将基本积分公式中的积分变量换成任 意一个可微函数,公式仍成立。例如将 cos sin x dx x C = + 中积分变 量 x 换做可微函数 2 3 5 + x ,则有 ( ) 2 2 2 cos 3 5 (3 5 ) sin (3 5 ) + + = + + x d x x C 【学生板演】例 3 计算不定积分 3 (3 8) x dx +

所以∫(3x+8)3d凑微分()「(3x+8)d( 元小) 。回代 积分公式( )+c} )+C 【学生板演】例4计算不定积分「2xed 换元 所以∫2xe凑微分∫e2xad )dhu 回代 积分公式( )+C )+C 【结论】“凑微分”的关键是把被积表达式分解成两部分,一部分为 复合函数几(x】,而另一部分凑成中间变量的微分 du=do(x)=p'(x)dk。在凑微分时,需熟悉微分的基本公式。在此 将一些常用的微分公式例举如下:
8 ( ) ( ) ( ) ( ) ( ) ( ) 3 3 (3 8) (3 8) ( ) ( ) x dx x d du C C + + + + 换元 所以 凑微分 回代 积分公式 【学生板演】例 4 计算不定积分 2 2 x x e dx ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 x x xe dx e xdx du C C + + 换元 所以 凑微分 回代 积分公式 【结论】 “凑微分”的关键是把被积表达式分解成两部分,一部分为 复 合 函 数 f x [ ( )] , 而 另 一 部 分 凑 成 中 间 变 量 的 微 分 du d x x dx = = ( ) ( ) 。在凑微分时,需熟悉微分的基本公式。在此 将一些常用的微分公式例举如下:

1.dk=。d(r+b)(a≠0,a与b均为常数) 2达==2石ar+)(a0a屿的为常数) 3.上=dnl0) 左=2a同=daG+b)(az0,a与的为常数 5. 61+文=(arcn) 7.e'dk=d(e) 8.cosxdx=d(sinx) 9.sinxdx=-d(cosx) 10. -x2 dx=d(arcsinx) 【板演】例5计算不定积分血太 凑微分 解因为上本=d血) 换元 所以∫hxdk=xxd(x)nx=ufudu -+c回+c 凑微分法运用熟练后,可省略换元步骤,直接写出结果。 9
9 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 2 1 1. 0, 1 1 2. 0, 2 2 1 3. ln 1 2 4. 2 0, 1 1 5. 1 6. arctan 1 7. 8. cos sin 9. sin cos 1 10. arcsin 1 x x dx d ax b a a b a xdx dx d ax b a a b a dx d x x dx d x d a x b a a b x a dx d x x dx d x x e dx d e xdx d x xdx d x dx d x x = + = = + = = = + = − = + = = = − = − 与 均为常数 与 均为常数 与 均为常数 【板演】 例 5 计算不定积分 ln x dx x ( ) ( ) ( ) 2 2 1 ln ln l ln ln ln ln 1 1 ln 2 2 dx d x x x dx x dx xd x x u udu x x u C x C = = = = = + + 解 因为 所以 回代 凑微分法运用熟练后,可省略换元步骤,直接写出结果。 凑微分 换元

例6计算不定积分osd x 凑微分 dh=2d 1 解fs5js回 =2sin√F+C 积分公式[cosxdx=sinx+C 4.2.2变量置换法 【讲解】需要计算的不定积分[f(x)dk形式虽然简单,但是却不易直 接求出。这时可适当选择x=w()进行变量置换,把不定积分 f(x)d转化为较容易计算的不定积分「f[w(u)]w'(u)du的形式。 这就是积分的变量置换法,也叫第二类换元积分法。 【核演】制11计草不定积分后一产 【分折】此不定积分的技积函数是无程分式一,此时我们能难 处理的根式部分√x-3作为一个整体,即令u=√x-3将无理式转化 为有理式,从而被积函数形式上得到简化。且有x=2+3.dk=2udu 代入原式有 g2a=e+恤-ac 再将u=√x-3回代,即可。 10
10 例 6 计算不定积分 cos x dx x ( ) cos 1 = cos 2 cos 2sin x dx x dx xd x x x x C = = + 解 4.2.2 变量置换法 【讲解】需要计算的不定积分 f x dx ( ) 形式虽然简单,但是却不易直 接求出。这时可适当选择 x u = ( ) 进行变量置换,把不定积分 f x dx ( ) 转化为较容易计算的不定积分 f u u du ( ) ( ) 的形式。 这就是积分的变量置换法,也叫第二类换元积分法。 【板演】 例 11 计算不定积分 3 x dx x − 【分析】 此不定积分的被积函数是无理分式 3 x x − ,此时我们把难 处理的根式部分 x −3 作为一个整体,即令 u x = −3 将无理式转化 为有理式,从而被积函数形式上得到简化。且有 2 x u dx udu = + = 3, 2 , 代入原式有 ( ) 2 3 2 2 3 2 2 3 6 3 u udu u du u u C u + = + = + + 再将 u x = −3 回代,即可。 凑微分 1 dx d x 2 x = cos sin xdx x C = + 积分公式