反常积分 在前面所讨时论的定积分事实上是有条件 的:一是积分区间是有限区间,二是被积函数 在积分区间上有界。但实际问题常常要突破这 两个前提,因此需要对定积分作如下两种推广 :无穷区间上的积分一无穷限积分,无界函 数在有限区间上的积分—无界函数积分或瑕 积分,统称为广义积分或旁义积分,以前讨论 过的定积分称为常义积分
反常积分 在前面所讨论的定积分事实上是有条件 的:一是积分区间是有限区间,二是被积函数 在积分区间上有界。但实际问题常常要突破这 两个前提,因此需要对定积分作如下两种推广 :无穷区间上的积分——无穷限积分,无界函 数在有限区间上的积分——无界函数积分或瑕 积分,统称为广义积分或旁义积分,以前讨论 过的定积分称为常义积分

一、无穷限的广义积分 定义1设函数f(x)在区间a,+o)上连续,取 b>a,如果极限imf(x)c存在,则称此极 b+00 限为函数f(x)在无穷区间[M,+oo)上的广义积 分,记作f(x)c. [f(x)dx =im ["f(x)dx 当极限存在时,称广义积分收敛;当极限不存在 时,称广义积分发散
定 义 1 设函数 f (x) 在区间[a,+)上连续,取 b a,如果极限 →+ b b a lim f (x)dx存在,则称此极 限为函数 f (x) 在无穷区间[a,+) 上的广义积 分,记作 + a f (x)dx. + a f (x)dx →+ = b b a lim f (x)dx 当极限存在时,称广义积分收敛;当极限不存在 时,称广义积分发散. 一、无穷限的广义积分

类似地,设函数f(x)在区间(-0,b]上连续,取 a<b,如果极限imf(x)存在,则称此极 限为函数f(x)在无穷区间(-o∞,b]上的广义积 分,记作”nf(x)dc. ∫fx)k=lim f(x) 当极限存在时,称广义积分收敛;当极限不存在 时,称广义积分发散
类似地,设函数 f (x) 在区间(−,b]上连续,取 a b,如果极限 →− b a a lim f (x)dx存在,则称此极 限为函数 f (x) 在无穷区间(−,b] 上的广义积 分,记作− b f (x)dx. − b f (x)dx →− = b a a lim f (x)dx 当极限存在时,称广义积分收敛;当极限不存在 时,称广义积分发散

设函数f(x)在区间(-0,+0)上连续,如果 广义积分f(x)和f(x)都收敛,则 称上述两广义积分之和为函数f(x)在无穷区间 (-o,+o)上的广义积分,记作nf(x). -limdx+iyd 极限存在称广义积分收敛;否则称广义积分发散
设函数 f (x) 在区间(−,+) 上连续,如 果 广义积分− 0 f (x)dx 和 + 0 f (x)dx 都收敛,则 称上述两广义积分之和为函数 f (x) 在无穷区间 (−,+)上的广义积分,记作 + − f (x)dx . →− = 0 lim ( ) a a f x dx →+ + b b f x dx 0 lim ( ) 极限存在称广义积分收敛;否则称广义积分发散

例1计算广义积分 -∞1+x2 解 = d + dx )1+x =▣+典14 6to01+2 -lim[aretanim arctanx →-∞ b)+00 2计算广义积分 解 sin -d
. 1 2 + − + x dx 解 + − + 2 1 x dx − + = 0 2 1 x dx + + + 0 2 1 x dx + = →− 0 2 1 1 lim a a dx x + + →+ b b dx x 0 2 1 1 lim 0 lim arctan a a x →− = b b arctan x 0 lim →+ + a a lim arctan →− = − b b lim arctan →+ + . 2 2 = + = − − 例2 计算广义积分 . 1 sin 1 2 2 + dx x x 解 + 2 1 sin 1 2 dx x x + = − 2 1 1 sin x d x 例1 计算广义积分
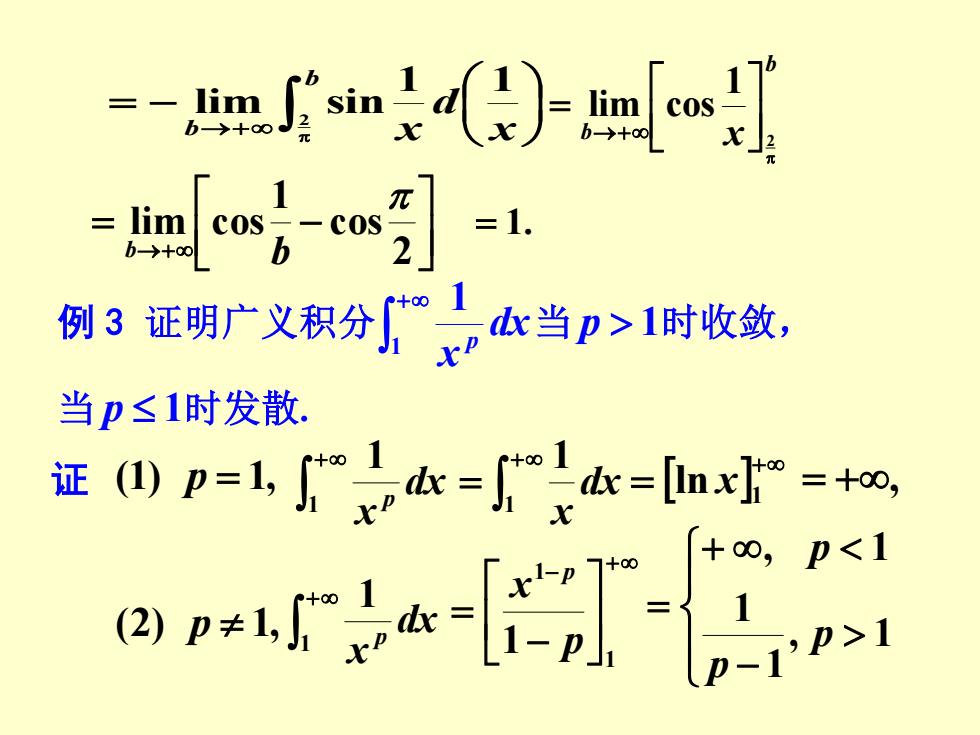
-tm.Jsin)-co w-co. 例3证明广义积分当p>1时收敛 当p≤1时发散. 证(0p=lc==血m=+o era-任 +∞,p<1
= − →+ b b x d x 2 1 1 lim sin b b x = →+ 2 1 lim cos = − →+ 2 cos 1 lim cos b b = 1. 例 3 证明广义积分 + 1 1 dx x p 当 p 1时收敛, 当 p 1时发散. 证 (1) p = 1, + 1 1 dx x p + = 1 1 dx x + = 1 ln x = +, (2) p 1, + 1 1 dx x p + − − = 1 1 1 p x p − + = , 1 1 1 , 1 p p p

因此当p>1时广义积分收敛,其值为 p-1 当p≤1时广义积分发散. 例4证明广义积分∫e当p>0时收敛, 当p0时收敛,当p<0时发散
因此当p 1时广义积分收敛,其值为 1 1 p − ; 当 p 1时广义积分发散. 例 4 证明广义积分 + − a p x e dx当 p 0时收敛, 当 p 0时发散. 证 + − a px e dx − →+ = b a px b lim e dx b a px b p e = − − →+ lim = − − − →+ p e p e pa pb b lim = − , 0 , 0 p p p e ap 即当p 0时收敛,当p 0时发散

二、无界函数的广义积分 定义2设函数f(x)在区间(4,b]上连续,而在 点的右邻域内无界.取ε>0,如果极限 Iim心ef(x)dc存在,则称此极限为函数f(r) 6→+0。 在区间(a,b上的广义积分,记作f(x)d. fx=limefx 当极限存在时,称广义积分收敛;当极限不存在 时,称广义积分发散
定义 2 设函数 f (x)在区间(a,b]上连续,而在 点a 的右邻域内无界.取 0 ,如果极限 →+ + b a f x dx lim ( ) 0 存在,则称此极限为函数f (x) 在区间(a,b]上的广义积分,记作 b a f (x)dx. b a f (x)dx →+ + = b a f x dx lim ( ) 0 当极限存在时,称广义积分收敛;当极限不存在 时,称广义积分发散. 二、无界函数的广义积分

类似地,设函数f(x)在区间,b)上连续, 而在点b的左邻域内无界.取ε>0,如果极限 mf(x)c存在,则称此极限为函数厂) 在区间M,b)上的广义积分, 记作f(x)=imf(x). 当极限存在时,称广义积分收敛;当极限不存在 时,称广义积分发散. 设函数f(x)在区间4,b]上除点c(M<c<b)外连 续,而在点c的邻域内无界.如果两个广义积分 f(x)c和f(x)都收敛,则定义
类似地,设函数 f (x) 在区间[a,b) 上连续, 而在点b 的左邻域内无界.取 0 ,如果极限 − →+ b a lim f (x)dx 0 存在,则称此极限为函数f (x) 在区间[a,b)上的广义积分, 记作 b a f (x)dx − →+ = b a lim f (x)dx 0 . 当极限存在时,称广义积分收敛;当极限不存在 时,称广义积分发散. 设函数 f (x)在区间[a,b]上除点c (a c b)外连 续,而在点c 的邻域内无界.如果两个广义积分 c a f (x)dx和 b c f (x)dx都收敛,则定义

Cf(x)dx=∫if(x)dx+∫f(x)dx n(d()d 否则, 就称广义积分f(x)c发散 定义中c为瑕点,以上积分称为瑕积分. 例5计算广义积分 x (a>0. 解 lim- =+00, x→a-0/a2-x2 ∴.x=为被积函数的无穷间断点 dx -8 dx a2-x2 lim[" 8-→+0J0 Va2-x2
b a f (x)dx = c a f (x)dx+ b c f (x)dx − →+ = c a lim f (x)dx 0 + →+ + b c f x dx lim ( ) 0 否则,就称广义积分 b a f (x)dx发散. 定义中c为瑕点,以上积分称为瑕积分. 例5 计算广义积分 ( 0). 0 2 2 − a a x a dx 解 , 1 lim 2 2 0 = + x→a− a − x x = a为被积函数的无穷间断点. − a a x dx 0 2 2 − →+ − = a a x dx 0 2 2 0 lim