
第三节 定定积分在物理学中的应用 前面我们已经介绍了定积分在几何方 面的应用,我们看到,在利用定积分解决几 何上诸如平面图形的面积、平面曲线的弧长、 旋转体的体积等问题时,关键在于写出所求 量的微元 定积分在物理方面的应用的关键也是 如此,希望大家注意如何写出所求量的微元 微功、微压力、微引力等
第三节 定积分在物理学中的应用 前面我们已经介绍了定积分在几何方 面的应用,我们看到,在利用定积分解决几 何上诸如平面图形的面积、平面曲线的弧长、 旋转体的体积等问题时,关键在于写出所求 量的微元 定积分在物理方面的应用的关键也是 如此,希望大家注意如何写出所求量的微元 ——微功、微压力、微引力等

一、变力沿直线作功 由物理学知道,如果一个物体在常力F 作用下,使得物体沿力的方向作直线运动, 物体有位移s时,力对物体所作的功为: W-F*s 这个公式只有在力F是不变的情况下才 适用,但在实际问题中,物体在运动过程中 所受到的力是变化的。下面我们通过例子来 说明如何利用微元法来求变力所作的功。 例1己知弹簧每伸长0.02m要用9,8N的力, 求把弹簧拉长0,1m需作多少功
由物理学知道,如果一个物体在常力F 作用下,使得物体沿力的方向作直线运动 , 物体有位移 s 时,力F对物体所作的功为: W=F*s 这个公式只有在力F是不变的情况下才 适用,但在实际问题中,物体在运动过程中 所受到的力是变化的。下面我们通过例子来 说明如何利用微元法来求变力所作的功。 例1 已知弹簧每伸长 0.02 m 要用 9,8 N 的力, 求把弹簧拉长 0,1 m 需作多少功 一、变力沿直线作功

解当我们拉长弹簧时,需要克服弹性力 作功,由Hoke定律,弹性力F与伸长 量x之间有函数关系:F=x k—弹性系数 由题设9.8=0.02k =490 F=490x 要求的是变力所作的功 用微元法 取x为积分变量积分区间为0,0.1] ∀[x,x+c0,0.1 弹簧由x处拉到x+处,由F化) 的连续性,当很小时,弹性力Fx)变 化很小,可近似地看作是不变的(常力)
当我们拉长弹簧时,需要克服弹性力 作功,由 Hoke 定律,弹性力F与伸长 量 x 之间有函数关系:F=kx k ——弹性系数 用微元法 由题设 9.8=0.02k k= 490 要求的是变力所作的功 F=490x 取 x 为积分变量 积分区间为 [0 ,0.1] [x, x + dx] [0,0.1] 弹簧由 x 处拉到 x +dx 处,由 F (x ) 的连续性,当 dx 很小时,弹性力F (x) 变 化很小,可近似地看作是不变的(常力) 解

于是在小区间x,x+心]上对应的变 力F所作的功近似于把变力F看作常力 F=490x所作的功 dW=F(x)dx=490xdx 0.1 W=490x=2.45 (J) 例2发射火箭需要计算克服地球引力所 作的功,设火箭的质量为m,问将火箭 垂直地向上发射到离地面高H时,需作 多少功。并由此计算初速度至少为多少 时,方可使火箭脱离地球的引力范围
于是在小区间 [x, x +dx ]上对应的变 力F所作的功近似于把变力F看作常力 F =490x 所作的功 dW = F(x)dx = 490xdx ( ) = = 0.1 0 W 490xdx 2.45 J 例2 发射火箭需要计算克服地球引力所 作的功,设火箭的质量为 m ,问将火箭 垂直地向上发射到离地面高H 时,需作 多少功。并由此计算初速度至少为多少 时,方可使火箭脱离地球的引力范围
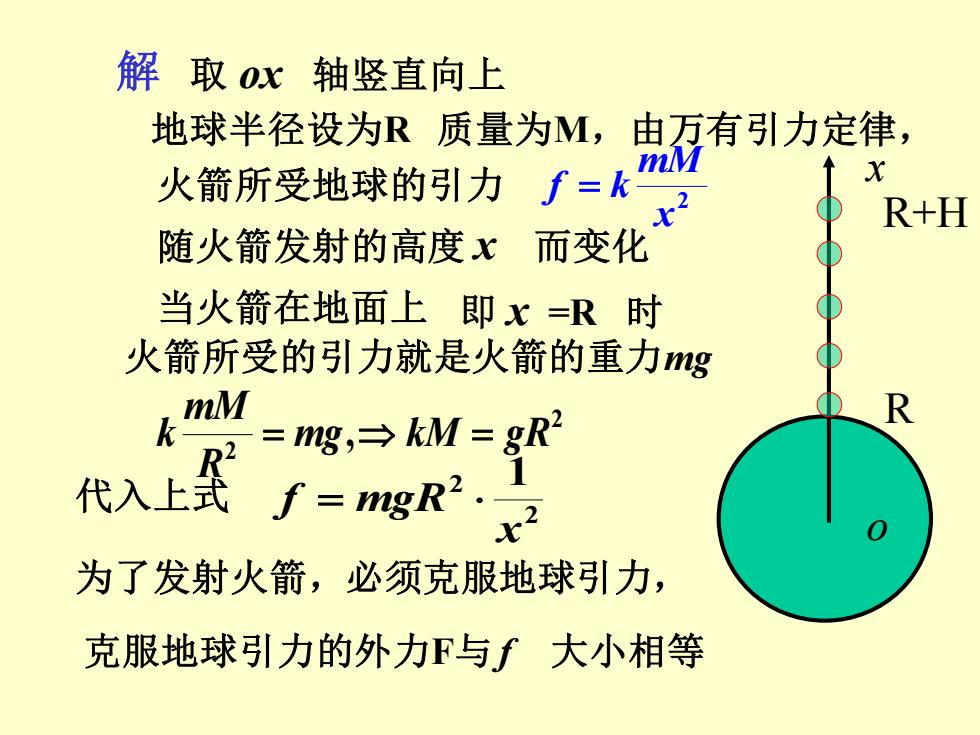
解取ox轴竖直向上 地球半径设为R质量为M,由万有引力定律, 火箭所受地球的引力∫=k X R+H 随火箭发射的高度x而变化 当火箭在地面上即x=R时 火箭所受的引力就是火箭的重力mg M k =g,→kM=gR2 代入上£f=mgR x2 为了发射火箭,必须克服地球引力, 克服地球引力的外力F与f大小相等
解 取 ox 轴竖直向上 x o R R+H 地球半径设为R 质量为M,由万有引力定律, 即 x =R 时 火箭所受的引力就是火箭的重力mg 2 x mM 火箭所受地球的引力 f = k 随火箭发射的高度 x 而变化 当火箭在地面上 2 2 mg, kM gR R mM k = = 代入上式 2 2 1 x f = mgR 为了发射火箭,必须克服地球引力, 克服地球引力的外力F与 f 大小相等

F()=gR2.1 下面用微元法来求变力所作的功。 取x为积分变量x∈[R,R+H] W=Fx)=mgR之 R+H 为了使火箭脱离地球引力范围,也 就是说要把火箭发射到无穷远处H→+∞ 所须作的功 w-mn-m心R(RR十甘=腾R H→+∞
2 2 1 ( ) x F x = mgR 下面用微元法来求变力所作的功。 x[R,R+ H] dx x dW F x dx mgR 2 2 1 = ( ) = dx x W mgR R H R H + = 2 2 1 ) 1 1 ( 2 R R H mgR + = − 取 x 为积分变量 mgR R R H w w mgR H H H = + = = − →+ →+ ) 1 1 ( 2 lim lim H → + 所须作的功 为了使火箭脱离地球引力范围,也 就是说要把火箭发射到无穷远处

这功是由火箭上的动能转化而来,若火箭 离开地面时的初速度为Vo 则动能为 2 2 因此要使火箭脱离地球引力范围,须有 m2sR≥2gR g=9.8×10-3km/s2,R=6371km 代入上式得≥11.2、—第二字宙速度
0 v 则动能为 2 0 2 1 mv 因此要使火箭脱离地球引力范围,须有 mv mgR 2 0 2 1 v0 2gR g 9.8 10 km s ,R 6371km 3 2 = = − 代入上式得 s v 11.2 km 0 ——第二宇宙速度 这功是由火箭上的动能转化而来,若火箭 离开地面时的初速度为

例3半径为R,高为H的圆柱形贮水桶,盛满了水, 问将水桶中的水全部吸出须作多少功? 这个问题虽然不是变力作功问题,但是由于吸 解 出同样重量不同深度的水时所作的功是不同的,所 以也要用定积分来计算。可以理解水是一层一层地 被吸到桶口的 在区间【yy+少】上对应一小薄柱体 该水柱重为Rdy 将这一小水柱提到桶口所经过的距离 H-y
半径为R,高为H 的圆柱形贮水桶,盛满了水, 问将水桶中的水全部吸出须作多少功? 解 这个问题虽然不是变力作功问题,但是由于吸 出同样重量不同深度的水时所作的功是不同的,所 以也要用定积分来计算。可以理解水是一层一层地 被吸到桶口的 在区间 [ y ,y + dy ] 上对应一小薄柱体 该水柱重为 R dy 2 将这一小水柱提到桶口所经过的距离 H − y 例3

dw=πR(H-y)d H →w=R∫H-J=7RH 将以上几例的解法一般化可得 若一物体在变力F(x) 的作用下,沿 力的方向(0x轴)作直线运动,当物体由 x=M移到x=b时,变力F(x) 对物体所作的功为 w=[F(x)dx
dw R (H y)dy 2 = − 2 2 0 2 2 w R (H y)dy R H H = − = 将以上几例的解法一般化 可得 若一物体在变力 F ( x ) 的作用下,沿 力的方向(ox 轴)作直线运动,当物体由 x = a 移到 x = b 时,变力 F ( x ) = b a w F(x)dx 对物体所作的功为

二、液体的侧压力 由物理学知道,一水平放置在液体中的薄板, 其面积为A,距液面的深度为,则该薄板的一 侧所受的压力P等于液体的压强卫与受力面积的 乘积,而压强等于深度与比重的乘积,于是 P=pA=yhA 但在实际问题中,往往需要计算与液面垂直放 置的薄板一侧的所受的压力,由于薄板在不同深度 处压强不同,因而不能直接应用上述公式进行计算, 需要采用微元法,利用定积分来计算。 例4设半径为R的圆形水闸门,水面与闸顶平齐, 求闸门一侧所受的压力
由物理学知道,一水平放置在液体中的薄板, 其面积为A,距液面的深度为 h ,则该薄板的一 侧所受的压力P等于液体的压强 p 与受力面积的 乘积,而压强等于深度与比重的乘积,于是 P = pA = hA 但在实际问题中,往往需要计算与液面垂直放 置的薄板一侧的所受的压力,由于薄板在不同深度 处压强不同,因而不能直接应用上述公式进行计算, 需要采用微元法,利用定积分来计算。 例4 设半径为R的圆形水闸门,水面与闸顶平齐, 求闸门一侧所受的压力。 二、液体的侧压力