
定积分的概念 前一章我们从导数的逆运算引出了不定积 分,系统地介绍了积分法,这是积分学的第一类 基本问题。本章先从实例出发,引出积分学的第 二类基本问题一定积分,它是微分(求局部量 )的逆运算(微分的无限求和一求总量),然 后着重介绍定积分的计算方法,它在科学技术领 域中有着极其广泛的应用。 重点 定积分的概念和性质,微积分基本公 式,定积分的换元法和分部积分法 难点 定义及换元法和分部法的运用
定积分的概念 前一章我们从导数的逆运算引出了不定积 分,系统地介绍了积分法,这是积分学的第一类 基本问题。本章先从实例出发,引出积分学的第 二类基本问题——定积分,它是微分(求局部量 )的逆运算(微分的无限求和——求总量),然 后着重介绍定积分的计算方法,它在科学技术领 域中有着极其广泛的应用。 重点 定积分的概念和性质,微积分基本公 式,定积分的换元法和分部积分法 难点 定义及换元法和分部法的运用

基车要求 ①正确理解定积分的概念及其实际背景 ②记住定积分的性质并能正确地运用 ③掌握变上限定积分概念,微积分基本定理, 并会用N-L公式计算定积分, ④能正确熟练地运用换元法和分部积分法 计算定积分 ⑤正确理解两类广义积分概念, 并会用定义计算一些较简单的广义积分
基本要求 ①正确理解定积分的概念及其实际背景 ②记住定积分的性质并能正确地运用 ③掌握变上限定积分概念,微积分基本定理, 并会用N-L公式计算定积分, ④能正确熟练地运用换元法和分部积分法 ⑤正确理解两类广义积分概念, 并会用定义 计算一些较简单的广义积分。 计 算定积分
一、问题的提出 实例1(求曲边梯形的面积) 求面积问题由来已久,对于由直线所围成的 平面图形的面积我们己经会求,下图所示的图形 如何求面积 m 将其置于直角 坐标系下考察 B 问题归结为AmBbaA与AnBbaA n 的面积之差 曲边梯形 0 bx
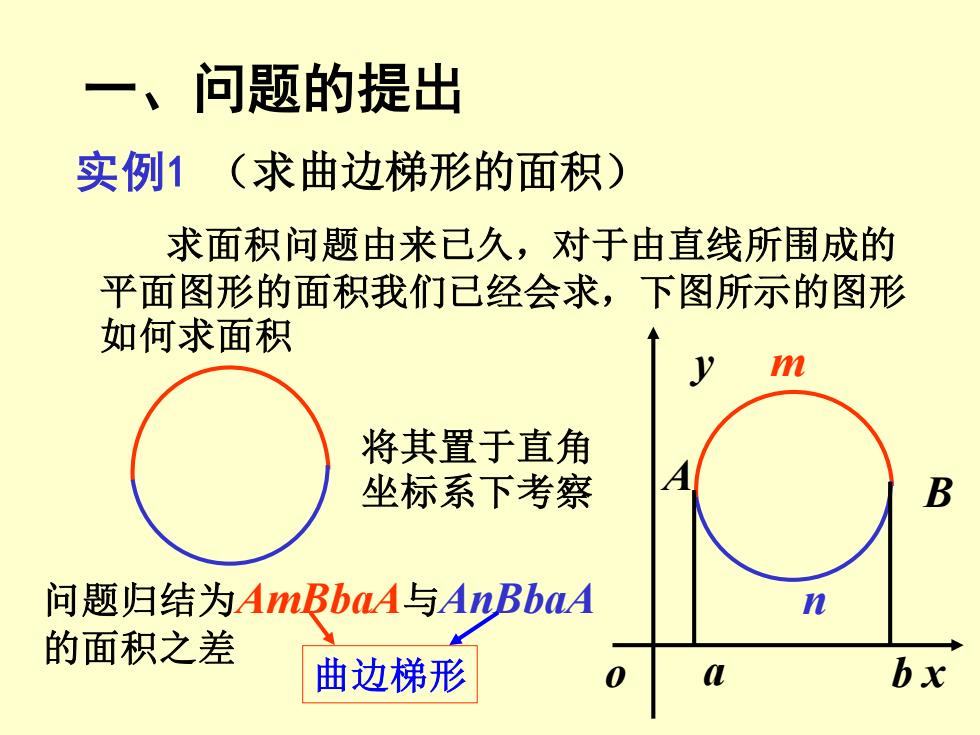
实例1 (求曲边梯形的面积) 求面积问题由来已久,对于由直线所围成的 平面图形的面积我们已经会求,下图所示的图形 如何求面积 将其置于直角 坐标系下考察 o x y a b A B m 问题归结为AmBbaA与AnBbaA n 的面积之差 曲边梯形 一、问题的提出
曲边梯形由连续曲线 y=f(x) 11 y=f(x)(f(x)≥0)、 x轴与两条直线x=M、 A=? x=b所围成. 用矩形面积近似取代曲边梯形面积
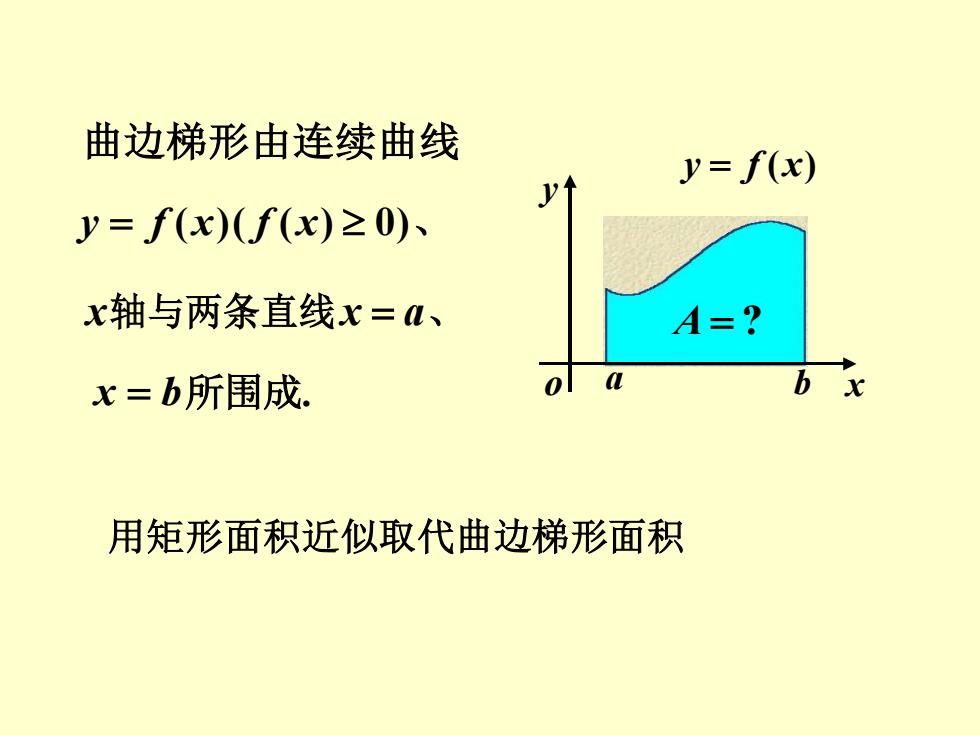
曲边梯形由连续曲线 y = f (x)( f (x) 0)、 x轴与两条直线x = a、 x = b所围成. a b x y o y = f (x) A = ? 用矩形面积近似取代曲边梯形面积
(四个小矩形) (九个小矩形) 显然,小矩形越多,矩形总面积越接近 曲边梯形面积. 观察下列演示过程,注意当分割加细时, 矩形面积和与曲边梯形面积的关系
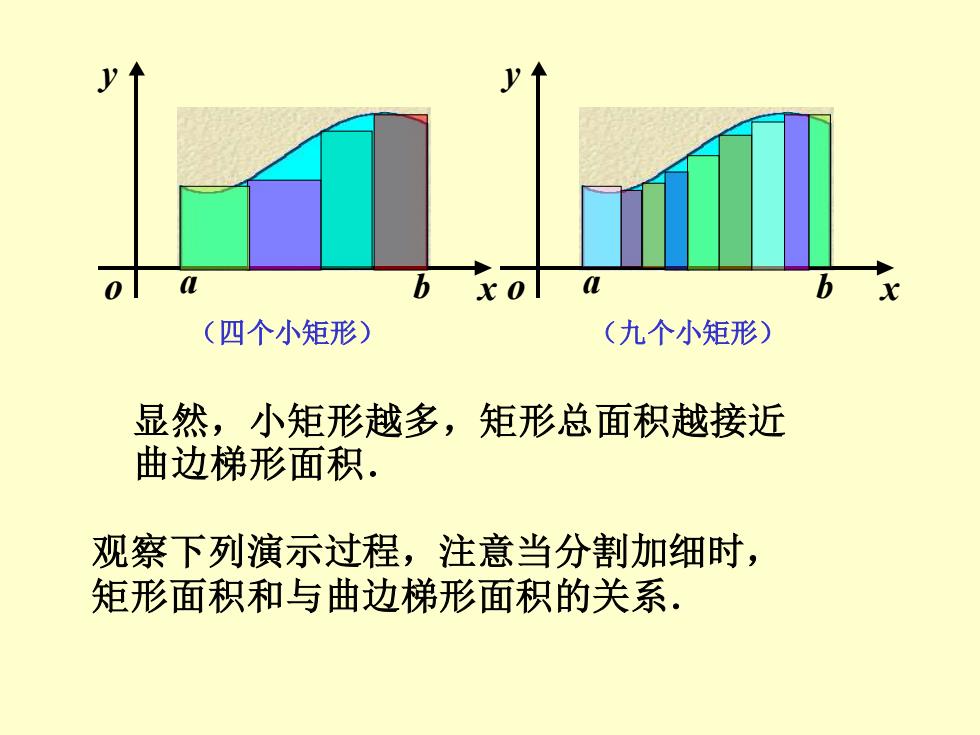
a b x y o (四个小矩形) a b x y o (九个小矩形) 显然,小矩形越多,矩形总面积越接近 曲边梯形面积. 观察下列演示过程,注意当分割加细时, 矩形面积和与曲边梯形面积的关系.

观察下列演示过程,注意当分割加细时, 矩形面积和与曲边梯形面积的关系. 3个分割点的图示 1.(上和-下和) 1.05556(积分近似值)
观察下列演示过程,注意当分割加细时, 矩形面积和与曲边梯形面积的关系. 播放

曲边梯形如图所示 在区间[a,b1内插入若干 个分点,M=x0<X1<x2<.<x-1<xn=b, 把区间[a,b]分成n 个小区间[-1,xb 长度为△x:=X,-X-9 在每个小区间[x-1,x】 上任取一点5 Xi-Exi 以[x-1,x为底,f(传)为高的小矩形面积为 A:=f(5:)△x
曲边梯形如图所示 a b x y o , [ , ] a x0 x1 x2 x 1 x b a b 个分点, = n− n = 在区间 内插入若干 ; [ , ] [ , ] 1 1 − − i = i − i i i x x x x x a b n 长度为 个小区间 , 把区间 分成 上任取一点 , i 在每个小区间 i xi xi [ , ] −1 x1 xi−1 xi xn−1 以[xi−1 , xi ]为底,f (i )为高的小矩形面积为 i i xi A = f ( )

曲边梯形面积的近似值为 A≈∑f(5:)△x i=1 当分割无限加细,即小区间的最大长度 2=max{△x1,△x2,.△xn} 趋近于零(九→0)时, 曲边梯形面积为A=lim∑f(传:)△r, i=1
曲边梯形面积的近似值为 i n i A f i x = ( ) 1 趋近于零 时, 当分割无限加细 即小区间的最大长度 ( 0) max{ , , } , 1 2 → = x x xn 曲边梯形面积为 i n i A = f i x = → lim ( ) 1 0

实例2(求变速直线运动的路程) 设某物体作直线运动,已知速度y=v(t)是 时间间隔[T,T,】上t的一个连续函数,且 v(t)≥0,求物体在这段时间内所经过的路程 思路:把整段时间分割成若干小段,每小段上 速度看作不变,求出各小段的路程再相加,便 得到路程的近似值,最后通过对时间的无限细 分过程求得路程的精确值
实例2 (求变速直线运动的路程) 设某物体作直线运动,已知速度v = v(t)是 时间间隔[ , ] T1 T2 上t 的一个连续函数,且 v(t) 0,求物体在这段时间内所经过的路程. 思路:把整段时间分割成若干小段,每小段上 速度看作不变,求出各小段的路程再相加,便 得到路程的近似值,最后通过对时间的无限细 分过程求得路程的精确值.

(1)分割T1=t<t1<t2<.<tn-1<tn=T3 △t:=t:-t1△S:≈y(△t 部分路程值 某时刻的速度 (2)求和s=∑4s,≈∑(c)4 i=1 (3)取极限 入=max{△t1,△t2,.,△tn} 路程的精确值s=m∑(;)△1 λ→0 i=1
1 0 1 2 1 T2 T t t t t t = n− n = i = i − i−1 t t t i i i s v( )t 部分路程值 某时刻的速度 (2)求和 i i n i n i i s s v( )t 1 1 = = = (3)取极限 max{ , , , } 1 2 n = t t t 路程的精确值 i n i i s = v t = → lim ( ) 1 0 (1)分割