
第三章导数的应用 3.1微分中值定理 3.1.1罗尔定理 一【定理讲述】定理1(罗尔定理)设函数(x)满足如下条件: )在闭区间【a,上连续: (2)在开区间(a,b)内可导: (3)fa)=fb)】 则在(a,b)内至少存在一点5,使得∫'()=0(a<5<b). 二几何意义 【作图、观察图像】设y=)是一条光滑曲线。 并且在点A,B处的纵坐标相等,即(a)=f(b) 那么可以看出,在弧AB上至少有一点C(5,(传》,其中a<5<b,曲线在 点C处的切线平行于x轴,即∫"(⑤)=0(图3.1.1D。 图3.1.1 例1设函数)=-2x-3,不求该函数的导数,说明方程 ∫"(x)=0有几个实根,并指出其所在的区间。 解由于x)=(x+1x-3),在-1,3]上连续,在(-1,3)内可导,且 八-)=f3)=0,故其在区间-1,]上满足罗尔定理的条件,所以至少存在
1 第三章 导数的应用 3.1 微分中值定理 3.1.1 罗尔定理 一 【定理讲述】定理 1(罗尔定理) 设函数 f (x) 满足如下条件: (1) 在闭区间 [a,b] 上连续; (2)在开区间 (a,b) 内可导; (3) f (a) = f (b); 则在 (a,b) 内至少存在一点 ,使得 f ( ) = 0 ( a b )。 二 几何意义 【作图、观察图像】设 y = f (x) 是一条光滑曲线, 并且在点 A, B 处的纵坐标相等,即 f (a) = f (b) , 那么可以看出,在弧 AB 上至少有一点 C (, f ( )) ,其中 a b ,曲线在 点 C 处的切线平行于 x 轴,即 f ( ) = 0 (图 3.1.1)。 o C a b A B f ( ) y = f (x) x y a b A B f ( ) y = f (x) x y a b A B f ( ) y = f (x) x y 图 3.1.1 例 1 设函数 ( ) 2 3 2 f x = x − x − ,不求该函数的导数,说明方程 f (x) = 0 有几个实根,并指出其所在的区间。 解 由于 f (x) = (x +1)(x − 3) ,在 [−1,3] 上连续,在 (−1,3) 内可导,且 f (−1) = f (3) = 0 ,故其在区间 [−1,3] 上满足罗尔定理的条件,所以至少存在

一点5∈(-山3),使得八⑤)=0,且广()是一-次函数,所以方程有且只有 一个实根。 3.1.2拉格朗日中值定理 一【定理讲述】定塞2(拉格朗日中值定理)设函数儿四)满足如下条件, ()在闭区间【a,b]上连续 (2)在开区间(a,)内可导: 则在(a,b)内至少存在一点5,使得 b-fa-f(⑤)a<5<b b-a 二几何意义 【作图、观察图像】在弧AB上除端点外处处具有不垂直于X轴的切线, 那么这弧上至少有一点C,,使曲线在C点处的切线平行于弦AB(图3.1.2)。 y■fx) 图3.1.2 推论1若∫)=0,re(a,b),则函数f)在(a,b)内是-个常数。 推论2若函数fx以8四)在开区间(a,b)内恒有f"()=8(),则在 (a,b)内f)与8()仅相差一个常数C,即f)=8+C, xE(a,b) 例2试用拉格朗日中值定理证明恒等式:sin'x+C0s2x=1,对于一切 x∈(-0,+o∞). 2
2 一点 (−1,3) ,使得 f ( ) = 0 ,且 f '(x) 是一次函数,所以方程有且只有 一个实根。 3.1.2 拉格朗日中值定理 一 【定理讲述】 定理 2(拉格朗日中值定理) 设函数 f (x) 满足如下条件: (1) 在闭区间 [a,b] 上连续; (2)在开区间 (a,b) 内可导; 则在 (a,b) 内至少存在一点 ,使得 ( ) ( ) ( ) ' f b a f b f a = − − , a b 二 几何意义 【作图、观察图像】在弧 AB 上除端点外处处具有不垂直于 x 轴的切线, 那么这弧上至少有一点 C ,使曲线在 C 点处的切线平行于弦 AB (图 3.1.2)。 a o b x y y = f (x) A C B x N M a o b x y o x y y = f (x) A C B x N M 图 3.1.2 推论 1 若 f (x) 0, x (a,b) , 则函数 f (x) 在 (a,b) 内是一个常数。 推论 2 若函数 f (x), g(x) 在开区间 (a,b) 内恒有 f (x) = g (x) ,则在 (a,b) 内 f (x) 与 g(x) 仅 相 差 一 个 常 数 C , 即 f (x) = g(x) +C , x (a,b) 。 例 2 试用拉格朗日中值定理证明恒等式: sin cos 1 2 2 x + x = ,对于一切 x (−,+)

证明设)=s加2x+c0sx,任取x∈(-0,+0),考患0与x之 间的闭区间,可知:)在该区间内满足拉格朗日中值定理的条件,所以有 fx)-f0=f() x-0 ,而f(x)=2snxc0sr-2 sin xc0sx=0,故 有f(x)=f0).即fx)=f0)=1. 【讲述】例3对函数y=x+血×在区间L,2]上验证拉格朗日中值定理. 解由于函数y=X+血x是初等函数,所以其在区向L,2]上选续,在开区 间山2)内可导,根据拉格朗日中值定理有: 2)-=f(5⑤) 2-1 即 1+h2=f(E). 3.1.3【了解】柯西定理 定理3(柯西定理)设函数)和8()满足条件: ()在闭区向a,1上连续: (2)在开区何(a,b)内可导 (3)g'(x)≠0(∈(a,b). f(b)-f(a)_f() 则在(a,b)内至少存在-一点5,使得8()-8a)g⑤),a<5<b】 作业:习题3.1一1、2③ 3.2洛必达法则 【于1口”是丙个无方小量之比的极,此根斑存在,头值为.而 一即也是两个无方小量之比的根限,但此极限不存在。我们把这类极跟多
3 证明 设 f x x x 2 2 ( ) = sin + cos ,任取 x (−,+) ,考虑 0 与 x 之 间的闭区间,可知 f (x) 在该区间内满足拉格朗日中值定理的条件,所以有 '( ) 0 ( ) (0) f x f x f = − − ,而 f '(x) = 2sin x cos x − 2sin x cos x = 0 ,故 有 f (x) = f (0) ,即 f (x) = f (0) = 1。 【讲述】例 3 对函数 y = x + ln x 在区间 [1,2] 上验证拉格朗日中值定理。 解 由于函数 y = x + ln x 是初等函数,所以其在区间 [1,2] 上连续,在开区 间 (1,2) 内可导, 根据拉格朗 日中值定理有: '( ) 2 1 (2) (1) f y y = − − ,即 1+ ln 2 = f ()。 3.1.3 【了解】柯西定理 定理 3( 柯西定理) 设函数 f (x) 和 g(x) 满足条件: (1)在闭区间 [a,b] 上连续; (2)在开区间 (a,b) 内可导; (3) g (x) 0 (x (a,b)) 。 则在 (a,b) 内至少存在一点 ,使得 '( ) '( ) ( ) ( ) ( ) ( ) = − − g f g b g a f b f a , a b 。 作业:习题 3.1—1、2③ 3.2 洛必达法则 【引子】 x x x sin lim →0 是两个无穷小量之比的极限,此极限存在,其值为 1,而 2 0 sin lim x x x→ 也是两个无穷小量之比的极限,但此极限不存在。我们把这类极限称

为未定式,记为0或巴。过去我们用恒等变形法,变量替换法等技巧,解决了 000 某些未定式的极限计算。 当女-0织=0,题得号起 式。 定理1(洛必达法则)设函数f(x)与g(x)满足条件: 4)mf)=0,1m8()=0: (2)f(x)与g(x)在点x的附近(点x。可除外)可导,且g(x)≠0: 虫得能a 唤得=8a (用中值定理的证明略) 定义1这种在一定条件下,通过对未定式的分子、分母分别求导再求极限的 方法,称为洛必达法则。 州1 解这是号型未定式用路经选法测附 g %:来吗到 0 解这是。型未定式,用洛必达法则得
4 为未定式,记为 0 0 或 。过去我们用恒等变形法,变量替换法等技巧,解决了 某些未定式的极限计算。 3.2.1 0 0 型未定式 当 lim ( ) 0, lim ( ) 0 0 0 = = → → f x g x x x x x 时,极限 ( ) ( ) lim 0 g x f x x→x 称为 0 0 型未定 式。 定理 1(洛必达法则) 设函数 f (x) 与 g(x) 满足条件: (1) lim ( ) 0, lim ( ) 0 0 0 = = → → f x g x x x x x ; (2) f (x) 与 g(x) 在点 0 x 的附近(点 0 x 可除外)可导 ,且 ( ) 0 / g x ; (3) ( ) ( ) lim / / 0 g x f x x→x 存在(或 ); 则 ( ) ( ) lim 0 g x f x x→x = ( ) ( ) lim / / 0 g x f x x→x (或 )。 (用中值定理的证明略) 定义 1 这种在一定条件下,通过对未定式的分子、分母分别求导再求极限的 方法,称为洛必达法则。 例 1 求极限 x x e x x − − → 1 3 lim 2 0 。 解 这是 0 0 型未定式,用洛必达法则得 x x e x x − − → 1 3 lim 2 0 1 1 6 1 1 lim 0 0 0 = − − = − − = → x x e x 例 2 求极限 2 0 ln(1 ) lim x x x + → 。 解 这是 0 0 型未定式,用洛必达法则得

“-克-2网 1 x2 1上送关于→无时日型米定武价备修达法测,对于→0时的 8装大适 例3求极限m。 arccotx 解这是号型未定式。用洛么达法则得 x2 @rotx即吓om平®争 y 注意2如果八①当x→时,仍属。型,且仍满足洛必达法则中的 8'x) 条件,那么可继铁应用洛必达法则进行计算,即m =lim f(x) 8(x) 6g(x) 三m。,依次类推,直到求出所要求的极限。 州4求限四产 解选是型未定大,用路达法侧烟 注意3若所求极限已不是未定式,则不能再应用洛必达法则,否则会导致错 误的结果
5 2 0 ln(1 ) lim x x x + → = + = = + = → + → → 2 (1 ) 1 lim 2 lim ( ) (ln(1 )) lim 0 1 1 0 2 / / 0 0 0 x x x x x x x x x 注意 1 上述关于 0 x → x 时, 0 0 型未定式的洛必达法则,对于 x → 时的 0 0 型未定式同样适用。 例 3 求极限 x x arc x 1 cot lim →+ 。 解 这是 0 0 型未定式,用洛必达法则得 x x arc x 1 cot lim →+ 1 1 lim 1 lim ) 1 ( ( cot ) lim 2 2 2 1 1 / / 2 0 0 = + = − − = = →+ + →+ →+ x x x x arc x x x x x 注意 2 如果 ( ) ( ) / / g x f x 当 0 x → x 时,仍属 0 0 型,且仍满足洛必达法则中的 条件,那么可继续应用洛必达法则进行计算,即 ( ) ( ) lim 0 g x f x x→x 0 0 = ( ) ( ) lim / / 0 g x f x x→x 0 0 = ( ) ( ) lim " " 0 g x f x x→x ,依次类推,直到求出所要求的极限。 例 4 求极限 3 0 sin lim x x x x − → 。 解 这是 0 0 型未定式,用洛必达法则得 3 0 sin lim x x x x − → 2 0 3 1 cos lim 0 0 x x x − = → 6 1 6 sin lim 0 0 0 = = → x x x 注意 3 若所求极限已不是未定式,则不能再应用洛必达法则,否则会导致错 误的结果

例5求极限snx 解这是日型未定式,但分子分母分别求导数后,将化为 0 cosx 此式震荡无极限,故洛必达法则失效,不能使用。但原极限存在,可用下法 limo sin x =msm 3.22日型未定式 当里了)=必巴g)=0时,展限回用为公型未 g(x) 定式 定理2(洛必达法则)设函数f(x)与g(x)满足条件: (1)lim f(x)=o,lim g(x)=o: (2)f(x)与g(x)在点x的附近(点x可除外)可导,且g(x)≠0: 3)nmf因存在(或为o g'(x) 典得得 对于x→0时的口型未定式,定理2同样成立,注意2,注意3,有类似 的结论。 6
6 例 5 求极限 x x x x sin 1 sin lim 2 →0 。 解 这是 0 0 型未定式,但分子分母分别求导数后,将化为 x x x x x cos 1 cos 1 2 sin lim 0 − → 此式震荡无极限,故洛必达法则失效,不能使用。但原极限存在,可用下法 求得 0 1 0 sin lim 1 lim sin sin 1 sin lim sin 1 sin lim 0 0 0 2 0 = = = = → → → → x x x x x x x x x x x x x x x 3.2.2 型未定式 当 = = → → lim ( ) , lim ( ) 0 0 f x g x x x x x 时,极限 ( ) ( ) lim 0 g x f x x→x 称为 型未 定式 定理 2 (洛必达法则)设函数 f (x) 与 g(x) 满足条件: (1) = = → → lim ( ) , lim ( ) 0 0 f x g x x x x x ; (2) f (x) 与 g(x) 在点 0 x 的附近(点 0 x 可除外)可导,且 ( ) 0 / g x ; (3) ( ) ( ) lim / / 0 g x f x x→x 存在(或为 ); 则 ( ) ( ) lim 0 g x f x x→x = ( ) ( ) lim / / 0 g x f x x→x (证明略)。 对于 x → 时的 型未定式, 定理 2 同样成立,注意 2,注意 3,有类似 的结论

例6求极限血xhx x2+1 解这是2型未定式,用洛必达法则得 2x limxlime x+msto x 例7求极限m 解这是”型未定式,用洛必达法则得 lim 6x 例8求极限mant 号tan3x 解这是2型未定式,用洛必达法则得 a2之 cos2x sin 2x= 6c0s6=3 2c0s2x 家强器 解这是”型未定式,用洛必达法则得 >
7 例 6 求极限 x x x x ln 1 lim 2 + →+ 。 解 这是 型未定式,用洛必达法则得 x x x x ln 1 lim 2 + →+ = + + →+ →+ = = x x x x x 1 2 lim ln 1 2 lim 例 7 求极限 x x e x 3 lim →+ 。 解 这是 型未定式,用洛必达法则得 x x e x 3 lim →+ 0 6 lim 6 lim 3 lim 2 = = →+ →+ →+ = = x x x x x x e e x e x 例 8 求极限 x x x tan 3 tan lim 2 → 解 这是 型未定式,用洛必达法则得 = → x x x tan 3 tan lim 2 0 0 2 2 2 2 2 2 cos cos 3 lim 3 1 3sec 3 sec lim = → → = x x x x x x = → 0 0 2 sin 2 sin 6 lim x x x 3 2cos 2 6cos 6 lim 2 = → x x x 例 9 求极限 x x x ln sin 5 ln sin lim →+0 。 解 这是 型未定式,用洛必达法则得

coSx sin x sin 5x 5cos5x=1 生4在未定式中,者m侣不在,不能指m侣不 8(x) 8(x) 在!此时应使用其他方法求限。一 =-1,但 ,极限不存在 x 作业:习题3.2:1-(1)(2) 3.3函数的极值 3.3.1函数的单调性 定理1设函数f)在(a,b)内可导, 0如果在(a,b)内∫"(x)>0,则f)在(a,b)内是单调递增的: ②如果在a,b)内f"(x)<0,则f()在a,b)内是单调递减的 ③如果在(a,b)内f'田)=0,则f四)在(a,b)内是常数. 定理1的几何意义非常清楚。见图3.3.1 8
8 1 cos 5cos5 lim 5 1 sin sin 5 lim 5 1 sin sin 5 lim cos5 cos lim 5 1 sin 5 5cos5 sin cos lim ln sin 5 ln sin lim 0 0 0 0 0 0 0 0 = = = = = →+ →+ →+ →+ →+ →+ x x x x x x x x x x x x x x x x x x x x 注意 4 在 0 0 或 未定式中,若 ( ) lim ( ) f x g x 不存在,不能断言 lim ( ) ( ) f x g x 不 存在!此时应使用其他方法求极限。例如 sin lim x x x → x − = −1 ,但 = − → x x x x (sin ) lim cos 1 lim x 1 x → − ,极限不存在。 作业:习题 3.2:1-(1)(2) 3.3 函数的极值 3.3.1 函数的单调性 定理 1 设函数 f (x) 在 (a,b) 内可导, ⑴ 如果在 (a,b) 内 f (x) 0 ,则 f (x) 在 (a,b) 内是单调递增的; ⑵ 如果在 (a,b) 内 f (x) 0 ,则 f (x) 在 (a,b) 内是单调递减的; ⑶ 如果在 (a,b) 内 f (x) = 0 ,则 f (x) 在 (a,b) 内是常数。 定理 1 的几何意义非常清楚。见图 3.3.1
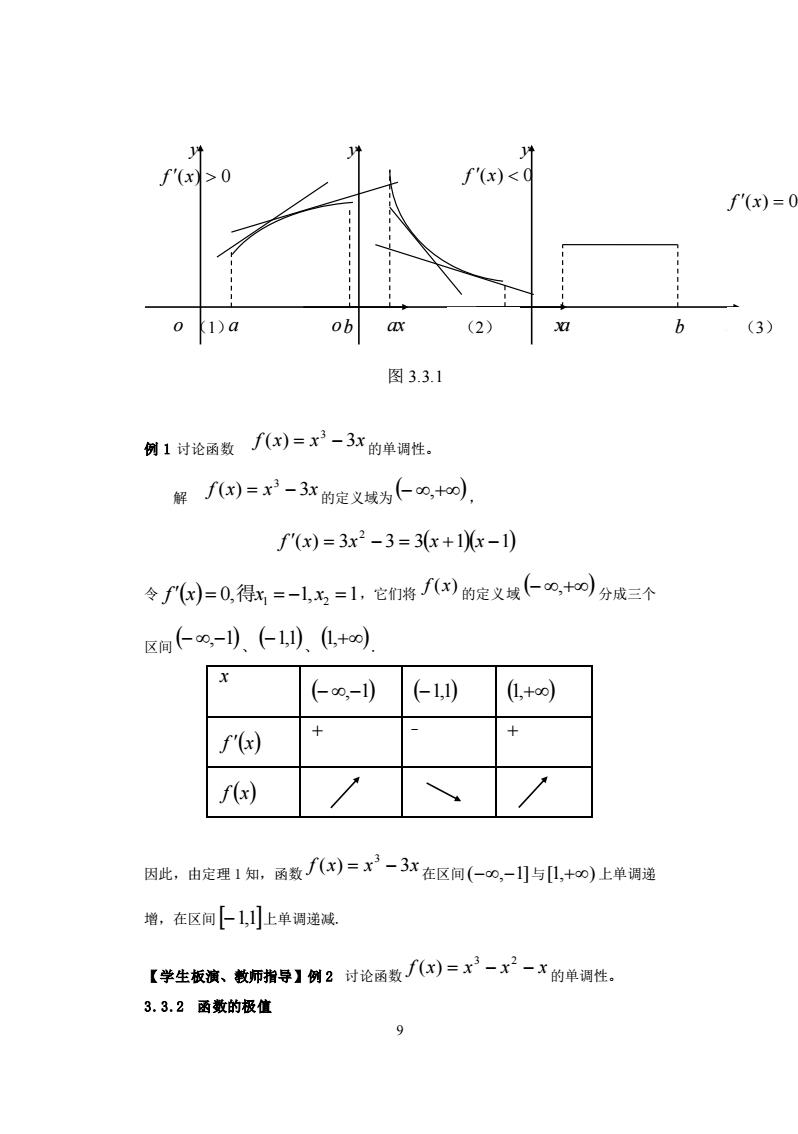
f'(x>0 f'(x)<0 f'(x)=0 01)a ob ax (2) (3) 图3.3.1 例1讨论函数(闭=x-3x的单调性。 解f)=2-3x的定文城为(0,+), f'(x)=3x2-3=3x+1x-1) 令∫()=0,得x=-1,玉=1,它们将f()的定义域仁0,+回)分成三个 区间人0,-).←1).L+o) (0,-1) (-1) (L,+oo) + f'(x) f(x) 因此,由定理1知,函数()=x-3江在区间(-0,-]与,+0)上单调递 增,在区间上1,上单调递减 【学生板演、教师指导】例2讨论函数)=-术一的单调性。 3.3.2函数的极值 9
9 例 1 讨论函数 f (x) x 3x 3 = − 的单调性。 解 f (x) x 3x 3 = − 的定义域为 (− ,+), ( ) 3 3 3( 1)( 1) 2 f x = x − = x + x − 令 f (x) = 0,得x1 = −1, x2 =1,它们将 f (x) 的定义域 (− ,+) 分成三个 区间 (−,−1)、 (−1,1)、 (1,+) . x (−,−1) (−1,1) (1,+) f (x) + - + f (x) 因此,由定理 1 知,函数 f (x) x 3x 3 = − 在区间 (−,−1] 与 [1,+) 上单调递 增,在区间 −1,1 上单调递减. 【学生板演、教师指导】例 2 讨论函数 f x = x − x − x 3 2 ( ) 的单调性。 3.3.2 函数的极值 o x y a b f (x) 0 f (x) 0 o x y a b f (x) = 0 图 3.3.1 o (1) x (2) (3) y a b
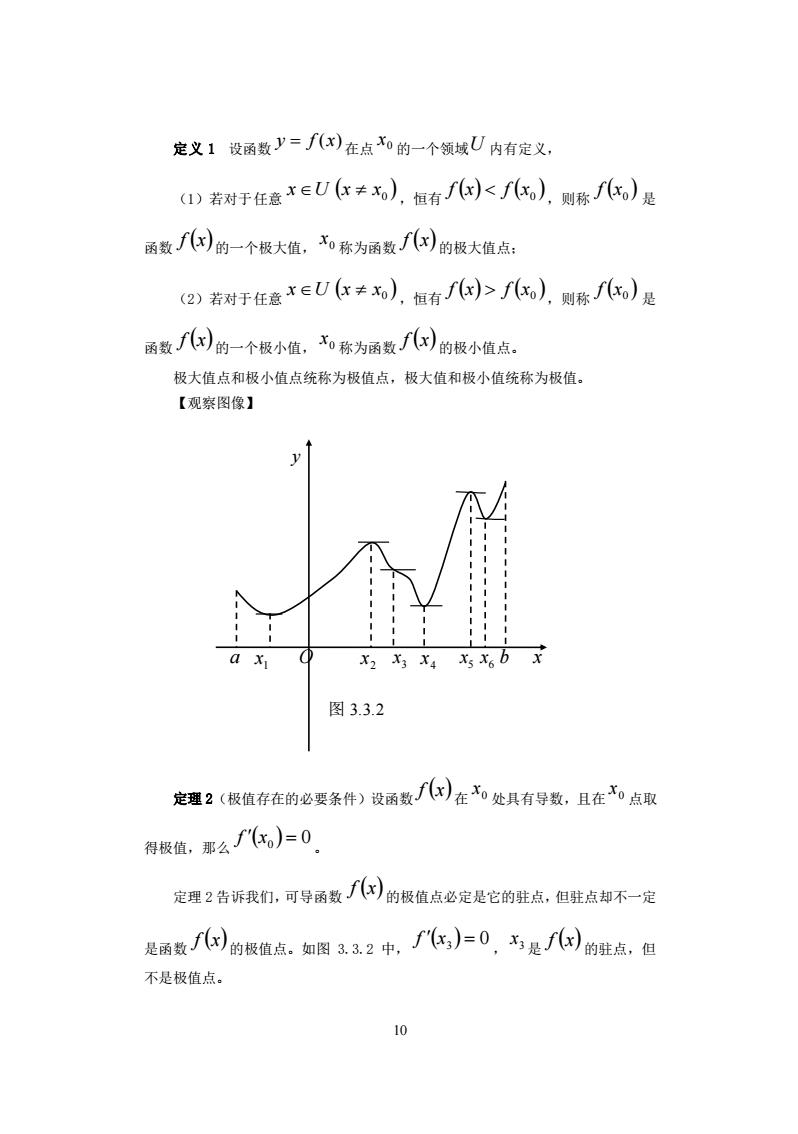
定义1设函数y=f)在点0的一个领城U内有定义, )若对于任意x∈U(≠x),恒有了)f),则陈f心,)是 函数儿)的一个极小值,0称为函数儿)的极小值点。 极大值点和极小值点统称为极值点,极大值和极小值统称为极值。 【观察图像】 a x x2x46b不 图3.3.2 定理2(极值存在的必要条件)设函数儿)在处具有导数,且在点取 得极值,那么代,)=0 定理2告诉我们,可号函数儿)的极值点必定是它的驻点,但驻点却不一定 是函数儿的极值点.如图33.2中,代,)=0,本是儿的驻点,但 不是极值点。 0
10 定义 1 设函数 y = f (x) 在点 0 x 的一个领域 U 内有定义, (1)若对于任意 ( ) 0 x U x x ,恒有 ( ) ( ) 0 f x f x ,则称 ( ) 0 f x 是 函数 f (x) 的一个极大值, 0 x 称为函数 f (x) 的极大值点; (2)若对于任意 ( ) 0 x U x x ,恒有 ( ) ( ) 0 f x f x ,则称 ( ) 0 f x 是 函数 f (x) 的一个极小值, 0 x 称为函数 f (x) 的极小值点。 极大值点和极小值点统称为极值点,极大值和极小值统称为极值。 【观察图像】 定理 2(极值存在的必要条件)设函数 f (x) 在 0 x 处具有导数,且在 0 x 点取 得极值,那么 f (x0 ) = 0。 定理 2 告诉我们,可导函数 f (x) 的极值点必定是它的驻点,但驻点却不一定 是函数 f (x) 的极值点。如图 3.3.2 中, f (x3 ) = 0 , 3 x 是 f (x) 的驻点,但 不是极值点。 图 3.3.2 a 1 x O 2 x 3 x 4 x 5 x 6 x b x y