
第十章重积分 §10-1二重积分的概念与性质 一、二重积分的概念 0曲顶柱体的体积v=一之f优,m△6 1.问题的提出(简述理由) (画图) (2)平面薄片的质量M=m∑p(5,n,)△6, 2.二重积分的定义(134页) 设f(x,)在D域上有界,细分D为几个小区域Aa, (I=1,2,3n)(表示区域及面积)若极限 lm∑f(5,n)Aa,,((,n)eAo,) 存在,则称该极限值为f(x,y)在D域上的二重积分,记为 ∬f(c,yda,或fcyd 即:∬f(,o=m∑f(5nAa 其中:川一一称为二重积分号,f(xy)一称为被积函 数D-一称为积分区域,do一一称为面积元素
1 第十章 重 积 分 §10-1 二重积分的概念与性质 一、二重积分的概念 1. 问题的提出 = = → = → n i i i i i n i i i M v f (2) lim ( , ) (1) lim ( , ) 0 1 0 平面薄片的质量 (简述理由) 曲顶柱体的体积 (画图) 2.二重积分的定义(134 页) 设 f(x,y) 在 D 域上有界 , 细 分 D 为几个小区域 i (I=1,2,3.n)(表示区域及面积)若极限 ( ) 0 lim , n i i i i f → ,( ( i i i , ) ) 存在,则称该极限值为 f(x,y)在 D 域上的二重积分,记为 ( , , , ) ( ) D D f x y d f x y dxdy 或 即: ( , ) D f x y d = ( ) 0 lim , n i i i i f → 其中: -称为二重积分号 , f(x,y)-称为被积函 数 D-称为积分区域 , d -称为面积元素

da didy 3.二重积分的几何意义一一曲顶柱体的体积 若f么)>0,则∬f(x,)do在几何上表示以曲面:=f(么)为 顶D域为底的曲顶柱体的积。 (物理意义)平面薄片的质量M=∬p(x,o 二、二重积分的性质:(类似定积分的性质) 1.∬kdo=松k为常数S为D域的面积下同) 当k=1时∬do=s 2.∬f(x,y)do=f(,y)do 玉.∬(c±方xo=rx)do±∬5(x4o 4.若D=DUD,则 ∬f(c,)do=∬f3y)do+∬fs,y)do 5.若f(x,y)≥g(x,y)(x,y)∈D 则「f(x,y)do≥叮g(x,y)do 特别地有-J川lf(x,y)川do川f(xy)do 7.(估值定理)若m≤f(x,y)≤M(x,y)eD 则ms≤∬f(x,y)do≤M6 8.(中值定理)若飞,y在D域上连续则在D内至少存在一点(5,7), 使得 f(x.y)do=f(s.n)-s 例1)设D域是由x=0,y=0,x+y=2用成,则3dG=. 2
2 d ( === dxdy 直角系) 。 3. 二重积分的几何意义-曲顶柱体的体积 若 f(x,y)>0,则 ( , ) D f x y d 在几何上表示以曲面 z = f(x,y)为 顶 D 域为底的曲顶柱体的积。 (物理意义) 平面薄片的质量 M = ( , ) D x y d 二 、二重积分的性质: (类似定积分的性质) 1. D kd ks = (k 为常数,S 为 D 域的面积,下同) 当 k=1 时 D d s = 2. ( , , ) ( ) D D kf x y d k f x y d = 3. [ , , ] , , 1 2 1 2 ( ) ( ) ( ) ( ) D D D f x y f x y d f x y d f x y d = 4. 若 D D D = 1 2 , 则 ( ) ( ) ( ) 1 2 , , , D D D f x y d f x y d f x y d = + 5. 若 f (x, y) g(x, y) (x, y)D 则 ( , , ) ( ) D D f x y d g x y d 特别地有- | , | | , | ( ) ( ) D D f x y d f x y d 7. (估值定理) 若 m f (x, y) M (x, y) D 则 ( , ) D ms f x y d Ms 8. (中值定理) 若 f(x,y) 在 D 域上连续,则在 D 内至少存在一点 (,), 使得 ( , , ) ( ) D f x y d f s = 例 1) 0, 0, 2 3 D D x y x y d = = + = = 设 域是由 围成,则

例2)(137页-4(2) 例3)(137页-5(4) 作业:(137页4(4);5(1) §10-2二重积分的什算 一、二重积分在直角坐标下的累次积分法 (把一个二重积分化为两次积分来计算的方法,称为累次积分法(或两次 积分法) 1、(矩形域)若积分域D为矩形域:a≤x≤b,C≤y≤d且 (x,y)在D域上连续,则 ∬fx,y)ddy=心dxfx,y)dy=dyfx,y)d (二重) (先y)(二次积分)(先x)(二次积分) 注明:1°f(x,y)dy=F(x,y)=F(x,d)-F(x,c) (x视为常数对y积分)(F=f(x,y) 2°f(x,y)k=p(x,y)北=p(b,y)-p(a,y) (y视为常数对x积分)(x,y)=f(xy) 例1)「(x2+2y)d少(两种次序求) 2)[x In ydxdy
3 例 2)(137 页-4(2)) 例 3)(137 页-5(4)) 作业:(137 页-4(4);5(1)) §10-2 二 重 积 分 的 计 算 一 、二重积分在直角坐标下的累次积分法 (把一个二重积分化为两次积分来计算的方法,称为累次积分法 (或两次 积分法)) 1、(矩形域)若积分域 D 为矩形域 : a x b , c y d 且 f (x, y) 在 D 域上连续,则 = = d c b a b a d c D f (x, y)dxdy dx f (x, y)dy dy f (x, y)dx 或 (二重) (先 y)(二次积分) (先 x)(二次积分) 注明: o 1 f (x, y)dy F(x, y)| F(x,d) F(x,c) d c d c = = − (x 视为常数对 y 积分) ( ( , )) ' F f x y y = o 2 ( , , | , , ) ( ) ( ) ( ) b b a a f x y dx x y b y a y = = − (y 视为常数对 x 积分) x ( x y f x y , , ) = ( ) 例 1) + 1 2 0 1 2 ( 2 ) y x x y dxdy (两种次序求) 2) y e x x ydxdy 1 0 4 ln

3)[ye"dxdy. 若fx,)=f)6)则 Ⅱ(5)=(()C5))(见154页-3题) D:1≤x≤23≤y≤4。 2、X型域)(D域的边界与垂直于x轴的直线相交不 多于两点的区域) y y=9(x) y=0(x) D y=x) b 若f(x,)在D域:a≤x≤b,g(x)≤y≤%(x)上连续, 则:∬x=fx炒 ≠xd。 3、(Y型域,(D域的边界与垂直于y轴的直线相交不多 于两点的区域)
4 3) 0 1 0 1 y x xy ye dxdy。 若 ( , ) ( ) ( ) 1 2 f x y = f x f y 则 1 2 1 2 ( ) ( ) ( ( ) )( ( ) ) b d a c a x b c y d f x f y dxdy f x dx f y dy = (见 154 页-3 题) 4) dxdy x y D − 2 ( ) 1 D : 1 x 2 3 y 4。 2 、(X 型域) (D 域的边界与垂直于 x 轴的直线相交不 多于两点的区域) 若 f x y ( , ) 在 D 域 : a x b , 1 2 ( x y x ) ( ) 上连续 , 则: = b a x x D f x y dxdy dx f x y dy ( ) ( ) 2 1 ( , ) ( , ) ( ) ( ) 2 1 ( , ) x x b a dy f x y dx 。 3、( Y 型域) (D 域的边界与垂直于 y 轴的直线相交不多 于两点的区域) 2 y x = ( ) a b D 1 y x = ( ) D b a 2 y x = ( ) 1 y x = ( ) D
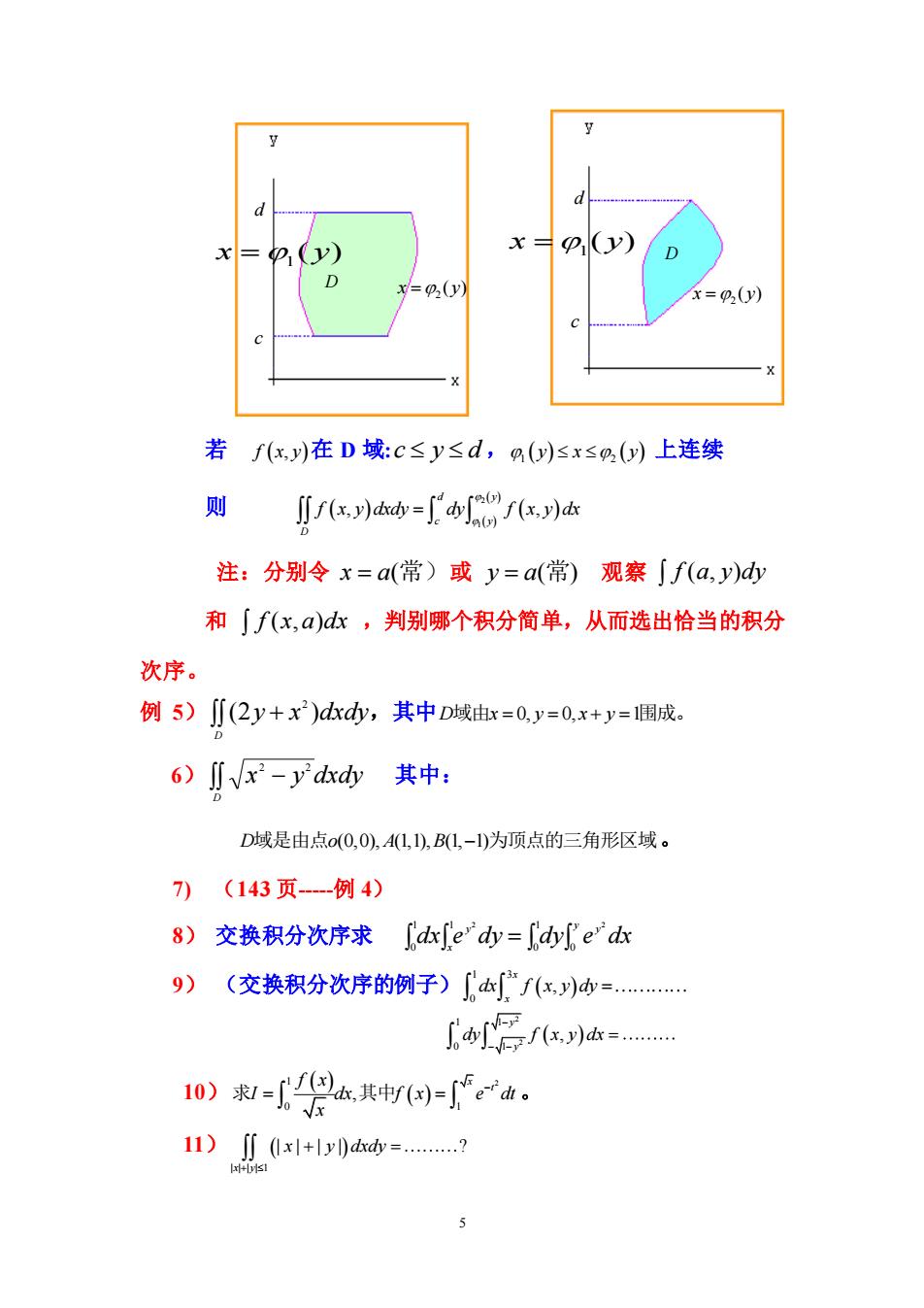
x=() xp(y) =(y) r=y) 若fx,)在D域:c≤y≤d,%)sx≤%)上连续 则 /列迹=了r列 注:分别令x=a(常)或y=a(常)观察∫f(a,y)dy 和∫f(x,a)dk,判别哪个积分简单,从而选出恰当的积分 次序。 例5)∬(2y+x)dkd少,其中D域由r=0,y=0,x+y=围成。 6)∬Vx-y dxdy其中: D域是由点o(0,0),4L,),BL,-)为顶点的三角形区域。 7)(143页-例4) 8)交换积分次序求dx[erdy=dy[e"dx 9)(交换积分次序的例子)f(s)=.。 fx,列k= 10)求=以但a其国ga DL010d=2
5 若 f x y ( , ) 在 D 域: c y d , 1 2 ( y x y ) ( ) 上连续 则 ( ) ( ) ( ) 2 ( ) 1 , , d y c y D f x y dxdy dy f x y dx = 注:分别令 x = a(常) 或 y = a(常) 观察 f (a, y)dy 和 f (x, a)dx ,判别哪个积分简单,从而选出恰当的积分 次序。 例 5) + D (2y x )dxdy 2 ,其中 D x y x y 域由 = = + = 0, 0, 1围成。 6) − D x y dxdy 2 2 其中: D o A B 域是由点 (0,0), (1,1), (1, 1) − 为顶点的三角形区域。 7) (143 页-例 4) 8) 交换积分次序求 dx e dy dy e dx y y x y = 1 0 0 1 1 0 2 2 9) (交换积分次序的例子) ( ) 1 3 0 , x x dx f x y dy = ( ) 2 2 1 1 0 1 , y y dy f x y dx − − − = 10) ( ) ( ) 1 2 0 1 , x t f x I dx f x e dt x − = = 求 其中 。 11) ( ) | | | | 1 | | | | ? x y x y dxdy + + = 2 x y = ( ) 1 x y = ( )D c d c d 2 x y = ( ) 1 x y = ( ) D

(另外奇偶性)(略) 1°若D关于x轴对称,则 「2fdy ∬fx,y)ddy= 0 f(x,y)为y的偶函数,f(x,一y)=+f(xy) f(x,y)为y的奇函数,f(x,-y)=-f(x,y) 2°若D关于y对称,则 0 ∬fcx,y)dd=2lfdy f(-x,y)=-f(x,y) f(-x,y)=f(x,y) 3°D关于原点对称,则 0 (dd 「f(-x,-y)=-f(x,y) f(-x,-y)=-f(x,y) 作业:(154-155页-1(3):2(3):6(5),(6):) 二、二重积分在极型标中的累次积分法 “极”与“直”的关系为:x=pcos8,y=psin或r+y广=p,=am0 且dc号hd号pdpd0(145页-说明) :极坐标中的二重积分变换公式为 6
6 (另外-奇偶性)(略) o 1 若 D 关于 x 轴对称,则 = 0 2 ( , ) D1 D fdxdy f x y dxdy f (x, y) 为 y 的偶函数, f (x,−y) = + f (x, y) f (x, y) 为 y 的奇函数, f (x,−y) = − f (x, y) o 2 若 D 关于 y 对称 ,则 = 1 2 0 ( , ) D D fdxdy f x y dxdy − = − = − ( , ) ( , ) ( , ) ( , ) f x y f x y f x y f x y o 3 D 关于原点对称,则 = 1 2 0 ( , ) D D fdxdy f x y dxdy − − = − − − = − ( , ) ( , ) ( , ) ( , ) f x y f x y f x y f x y 作业:(154-155 页-1(3);2(3);6(5),(6);) 二、 二重积分在极坐标中的累次积分法 “极”与“直”的关系为: 2 2 2 cos , sin , , tan y x y x y x = = + = = 或 且 ( d dxdy d d (直) 极) (145 页-说明) 极坐标中的二重积分变换公式为

∬f(x,)kd=j∬r(psin0)pdpd0 1.若Das0sB (极点在D域外) 9()≤p≤p(0) (i)dpdosin) 2.若D0≤0s2n (极点在D域内) 0sp≤p(a) (pcos.psin)pdpdodof(ossin)pdp 一般上,若()积分域D是圆形域、或环形域、或扇形域: (②)被积函数fx,y)含有2+y2或因子。 则选用极坐标求二重积分,其它情形选“直”求。 举例:12)小Vx2+y2dd D:x2+y2≤25 13)∬e-h D:x2+y2≤a2(顺便提一下P148 的概率积分) l4∬arctg D={(x,y)川1≤x2+y2≤4,y20,y≤x} 15)“直”与“极”的转化的例子 刚fk 作业:(155-156页-12(3);14(2):15(2) *三、二重积分的换元法(略)
7 ( , cos , sin ) ( ) D D f x y dxdy f d d = 1.若 1 2 ( ) ( ) D (极点在 D 域外) 则 ( ) ( ) ( ) 2 ( ) 1 cos , sin cos , sin D f d d d f d = 2.若 ( ) 0 2 0 D (极点在 D 域内) 则 ( ) ( ) 2 ( ) 0 0 cos , sin cos , sin D f d d d f d = 一般上,若 ⑴积分域 D 是圆形域、或环形域、或扇形域; ⑵被积函数 x y f (x, y)含有x 2 + y 2或 因子。 则选用极坐标求二重积分,其它情形选“直”求。 举例:12) x y dxdy D + 2 2 : 25 2 2 D x + y 13) e dxdy D x y −( + ) 2 2 2 2 2 D : x + y a (顺便提一下 P148— 的概率积分) 14) dxdy x y arctg D ( ) 2 2 D x y x y y y x = + , |1 4, 0, 15) “直”与“极”的转化的例子 ( ) 2 ( 1 1 0 1 , y y dy f x y dx − − = 极) 作业:(155-156 页-12(3);14(2);15(2)) *三 、二重积分的换元法(略)

定理设fx,y)在xoy平面上的闭区城D上 连续,变换T:x=x(u,y=y(,) 将uov平面上的闭区域D变为xoy平面上的D: 且满足 (①)x(u,y),y(4,y)在D上具有一阶连续偏导数 2在D上雅可比式Ju,= (u,y) (3)变换T:D→D是一对一的,则有 fx=u,以Wuh. 工页下园区回 例1计算川e*dcd其中D由x轴、轴和直 线x+y=2所围成的闭区域, 解令u=y-x,v=y+x, 则x=“ 2 y=+ 2 D→D,即x=0→u=-y y=0→4= x+y=2→y=2
8 ( , ) [ ( , ), ( , )] ( , ) . (3) : 0; ( , ) ( , ) (2) ( , ) (1) ( , ), ( , ) : ( , ), ( , ) ( , ) = → = = = D D f x y dxdy f x u v y u v J u v dudv T D D u v x y D J u v x u v y u v D uov D xoy D T x x u v y y u v f x y xoy D 变 换 是一对一的,则有 在 上雅可比式 在 上具有一阶连续偏导数; 且满足 将 平面上的闭区域 变 为 平面上的 , 连续,变换 定 理 设 在 平面上的闭区域 上 例1 解 线 所围成的闭区域. 计算 其中 由 轴、 轴和直 2 , + = + − x y e dxdy D x y D y x y x 令 u = y − x, v = y + x, . 2 , 2 v u y v u x + = − 则 = D → D , D x y o x + y = 2 D u v o u = −v u = v v = 2 2 2. 0 ; 0 ; + = → = = → = = → = − x y v y u v 即 x u v

J- a(4,) 22 故小e=小ena -dLidu-C(e-e)-e-e 工列下园国回 例2 计第,1-多a,其中D为 新可形+若-1所留度的闲区装 解 作广义极坐标变换r=rcos0, y=brsin0. 其中a>0,b>0,r≥0,0≤0≤2元 在这变换下D→D'={(r,0)0≤r≤1,0≤0≤2π, 园回回 9
9 ( , ) ( , ) u v x y J = , 2 1 2 1 2 1 2 1 2 1 = − − = + − = − D v u D y x y x e dxdy e dudv 2 1 故 − = v v v u dv e du 2 2 0 1 − = − 2 0 1 ( ) 2 1 e e vdv . −1 = e − e 例2 解 椭 圆 所围成的闭区域. 计 算 其 中 为 1 1 , 2 2 2 2 2 2 2 2 + = − − b y a x dxdy D b y a x D 其中a 0, b 0, r 0, 0 2. = = sin , cos , y br x ar 作广义极坐标变换 在这变换下D → D = {(r,)0 r 1 , 0 2}

即计择小号,共中D为 精圆后+长-1所图成的闲区线, 解 作广义极坐标变换r=arcos0, y =brsine, 其中a>0,b>0,r20,0≤0≤2π. 在这变换下D→D'={r,)0≤r≤1,0≤0≤2π, 工页下园区回 §10—3三重积分的橇念及其计算方法 三重积分的概念与性质 1.三重积分的定义(157页一略) (定积分) (二重积分) (三重积分) f本f(.)da∬fkw =2f(⑤)Ay-2f⑤,n)Aa, -lm2f(5,5)Ay 注明:1°-一积分的体积元素: 2°.几何意义随着概念的推广而消失
10 例2 解 椭 圆 所围成的闭区域. 计 算 其 中 为 1 1 , 2 2 2 2 2 2 2 2 + = − − b y a x dxdy D b y a x D 其中a 0, b 0, r 0, 0 2. = = sin , cos , y br x ar 作广义极坐标变换 在这变换下D → D = {(r,)0 r 1 , 0 2}, §10─3 三重积分的概念及其计算方法 一. 三重积分的概念与性质 1.三重积分的定义 (157 页-略) (定积分) (二重积分) (三重积分) ( ) b a f x dx ( ) ( ) ( ) , , , f x f x y a b D D f x y d → ⎯⎯⎯⎯⎯→ → ( ) ( ) ( ) , , , , , f x y f x y z D f x y z dV → → ⎯⎯⎯⎯⎯⎯→ ( ) 0 1 lim n i i i f x → = = = ( ) 0 1 lim , n i i i i f → = = ( ) 0 1 lim , , n i i i i i f V → = 注明: 1 .dv 0 -积分的体积元素; 2 . 0 几何意义随着概念的推广而消失