
第三章导数与微分 教学要求()理解导数的概念和导数的几何意义,会求平面曲线的切线方程 和法线方程:理解函数的可导与连续性之间的关系:了解高 阶导数的概念 高阶导数 (2课时) ②米提基本初等函数的求导公式,导数的四则运算法则、复 数及隐函数的求导法则。(2课时) (3)理解一元函数微分的概念,理解可微与可导之间的关系,掌握 微分的运算方法,了解微分在近似计算中的应用。(2课时) 教学重点导数的概念及几何意义:导数的四则运算法则、复合函数求导法 则和隐函数求导法:微分的概念 教学难点导数的概念,复合函数、反函数、隐函数求导法则 第一节函数的局部变化率一导数 抽象导数概念的两个现实原型 我们在解决实际问题时,除了需要了解变量之间的函数关系以外,有时还需 要研究变量变化快慢的程度例如物体运动的速度,城市人口增长的速度,国民 经济发展的速度等。其中三类问题导致了微分学的产生: 1:求变速运动的瞬时速度2:求曲线上一点处的切线3:求极大值和极小值 原型】求变速直线运动的瞬时速度 有一质点以O为原点做变速直线运动,用s表示质点运动的路程,s是时间t的 函数,记作s=f),1e0,T可,求。∈0,T门时刻的瞬时速度. 分析:匀速直线运动中=,变速直线运动不能直接用公式,速度的变与不变如 何解决? 解决步骤:(1)求增量:给。一个增量△1,时间从。变到了1=4,+△1,路程增量 △s=f4)-f()=f(+△)-f) (2)求增量比:当△1很小时,质点在该时间段内的运动可近似的看成匀速运 动,则△内的平均速度 =△s=f,+△)-f6) (3)取极限:当△越来越小,平均速度越来越接近于1,时刻的瞬时速度.于 是△1→0时,平均速度的极限就是瞬时速度,即 %产细名 、f(。+)-f) At
1 第三章 导数与微分 教学要求 (1) 理解导数的概念和导数的几何意义,会求平面曲线的切线方程 和法线方程;理解函数的可导与连续性之间的关系;了解高 阶导数的概念,会求简单函数的高阶导数。(2 课时) (2) 掌握基本初等函数的求导公式,导数的四则运算法则、复合函 数及隐函数的求导法则。(2 课时) (3) 理解一元函数微分的概念,理解可微与可导之间的关系,掌握 微分的运算方法,了解微分在近似计算中的应用。(2 课时) 教学重点 导数的概念及几何意义;导数的四则运算法则、复合函数求导法 则和隐函数求导法;微分的概念 教学难点 导数的概念,复合函数、反函数、隐函数求导法则 第一节 函数的局部变化率——导数 一、 抽象导数概念的两个现实原型 我们在解决实际问题时,除了需要了解变量之间的函数关系以外,有时还需 要研究变量变化快慢的程度.例如物体运动的速度,城市人口增长的速度,国民 经济发展的速度等。其中三类问题导致了微分学的产生: 1:求变速运动的瞬时速度 2:求曲线上一点处的切线 3:求极大值和极小值 原型Ⅰ 求变速直线运动的瞬时速度 有一质点以 O 为原点做变速直线运动,用 s 表示质点运动的路程,s 是时间 t 的 函数,记作s ft t = ∈ ( ), [0,T],求 0t ∈[0,T]时刻的瞬时速度. 分析:匀速直线运动中 = s v T ,变速直线运动不能直接用公式,速度的变与不变如 何解决? 解决步骤:(1)求增量:给 0t 一个增量Δt ,时间从 0t 变到了tt t 1 0 = +Δ ,路程增量 10 0 0 Δ = = +Δ s ft ft ft t ft ( )- ( ) ( )- ( ). (2)求增量比:当Δt 很小时,质点在该时间段内的运动可近似的看成匀速运 动,则Δt 内的平均速度 0 0 ( )- ( ) = =s f t t ft v t t Δ + Δ Δ Δ . (3)取极限:当Δt 越来越小,平均速度越来越接近于 0t 时刻的瞬时速度. 于 是Δ →t 0 时,平均速度的极限就是瞬时速度,即 0 0 0 t0 t0 t0 ( )- ( ) = lim = lim = lim s f t t ft v v t t Δ→ Δ→ Δ→ Δ + Δ Δ Δ

原型Ⅱ求曲线切线的斜率 M(x,y)和M(x,y)是曲线y=f(x)上两点,它们的 连线是该曲线的一条割线.当点M沿曲线无限接近 于点M,时,割线绕点M,转动,其极限位置M,T就 是曲线在点M。处的切线(图3.1),求曲线在点M。处 切线的斜率。 分析:若)=)的图像为直线。则斜率=然 y=(x)的图像为曲线,如何用直线的斜率来解决? 和十△r 解决步骤: (1)求增量:给x。一个增量△x,自变量由变到+△x,则 △y寸f(x+△x)-f(x,) (2)求增量比:Ay=f+Ax)f △r △r (》取极限:aa=一是-▣化+a-其中aa受是切线 △ M。T与x轴的夹角 总结:上面两个现实原型的范畴虽不相同,但从纯数学的角度来考察,所要解决 的问题相同:求一个变量相对于另一个相关变量的变化快慢程度,即变化率问题: 处理问题的思想方法相同:矛盾转化的辨证方法:数学结构相同:函数改变量与 自变量改变之比,当自变量改变量趋于零时的极限。由这两个具体问题便可抽 象出导数的概念 二、导数的概念 1.定义:设函数y=f(x)在点x,的某一邻域内有定义,当自变量x在x。处有 增量△x(点x,+△x仍在该邻域内)时,相应地函数有增量Ayf(x+A)-f(), 如果当△→0时,架的樱限存在,则移这个极限值为)y=在点气处的导数, 记作儿,即 儿是+园 (3.1) Ar 也可记作了(G).安或妥 如果极限(3.1)存在,则称函数fx)在点x处可导:如果极限(3.1)不存在, 2
2 原型 II 求曲线切线的斜率 M (, ) x y 和 0 M (, ) x y 是曲线 y = f x( ) 上两点,它们的 连线是该曲线的一条割线.当点 M 沿曲线无限接近 于点M0 时,割线绕点 M0 转动,其极限位置M0 T 就 是曲线在点M0 处的切线(图 3.1),求曲线在点M0 处 切线的斜率. 分析:若 y fx = ( ) 的图像为直线,则斜率 = y k x Δ Δ . y = f x( ) 的图像为曲线,如何用直线的斜率来解决? 解决步骤: (1) 求 增 量 : 给 0 x 一个增量 Δx ,自变量由 0 x 变 到 x0+Δx , 则 = ( )- ( ) 0 0 Δ +Δ y fx x fx (2) 求增量比: 0 0 ( )- ( ) =y f x x fx x x Δ + Δ Δ Δ . (3) 取极限: 0 0 0 0 ( ) () tan lim lim Δ→ Δ→ Δ + Δ − = = x x Δ Δ y f x x f x x x α . 其中 ( ) 2 π α α ≠ 是切线 M0 T 与 x 轴的夹角. 总结:上面两个现实原型的范畴虽不相同,但从纯数学的角度来考察,所要解决 的问题相同:求一个变量相对于另一个相关变量的变化快慢程度,即变化率问题; 处理问题的思想方法相同;矛盾转化的辨证方法;数学结构相同:函数改变量与 自变量改变之比,当自变量改变量趋于零时的极限. 由这两个具体问题便可抽 象出导数的概念。 二、导数的概念 1. 定义: 设函数 y = f x( ) 在点 0 x 的某一邻域内有定义,当自变量 x 在 0 x 处有 增量Δx (点 x0+Δx 仍在该邻域内)时,相应地函数有增量 = ( )- ( ) 0 0 Δy fx x fx + Δ , 如果当Δ →x 0时, y x Δ Δ 的极限存在,则称这个极限值为 y fx = ( ) 在点 0 x 处的导数, 记作 = 0 ' x x y ,即 0 0 0 0 0 ( )- ( ) ' | = lim = lim x x x x y f x x fx y x x = Δ→ Δ→ Δ + Δ Δ Δ . (3.1) 也可记作 0 f ' ( ) x , = 0 x x dy dx 或 = 0 ( ) x x d f x dx . 如果极限(3.1)存在,则称函数 f ( ) x 在点 0 x 处可导;如果极限(3.1)不存在

则称函数f(x)在点x,处不可导. 注:0.密表示导数的一个整体行号。 (②).导数是平均变化率的极限!导数的力学意义是变速直线运动物体的瞬时 速度:导数的几何意义是曲线切线的斜率。 2.求导数步骤与例题: (1)给x一个增量△x,则函数增量△f(x+A-f(x月 (2)求平均变化率y-f伍+Af): △r 3))求平均变化幸的极限儿-四是回 △x 例1.求函数f(x)C(常数)在x,点的导数 解:)=+Af_CC-0.即常数的导数为零 △r △r 例2.求函数f(x)=x在点x=2的导数. 解:给x=2一个增量△x,则函数增量为△y=(2+△x)2-2=4△r+(△x)2.平均变化 率为袋4+于是)-是-四4+a=4 Ar 说明:如果函数y=f(x)在区间(a,b)内的每一点处都可导,则称函数y=f(x)在 区间(a,b)内可导,且称f(x)为函数y=fx)的导函数.显然函数y=fx)在点 x,处的导数f(x),就是导函数∫(x)在x处的函数值,即∫(x)=∫(x) 例3.求函数)=在x处的导数. 解:先求导函数。给任意一点x一个增量A,得到A+Axx+A) 11-△x 所以y=巴是-把A子再求处的导数(礼引 -1 例4.求函数y=√F的导数 解:任取一点x∈(0,+o)一个增量△x,得到△y=√+△x-√F 是 1 ArVx+△r+V 所以y=四然=+xG2g 说明:由前面的三个例子发现,幂函数的导数公式(xy=ax(a为任一实数) 3
3 则称函数 f ( ) x 在点 0 x 处不可导. 注:(1). dy dx 表示导数的一个整体符号. (2).导数是平均变化率的极限!导数的力学意义是变速直线运动物体的瞬时 速度;导数的几何意义是曲线切线的斜率. 2. 求导数步骤与例题: (1) 给 0 x 一个增量Δx ,则函数增量 = ( )- ( ) 0 0 Δy fx x fx + Δ ; (2) 求平均变化率 0 0 ( )- ( ) =y f x x fx x x Δ + Δ Δ Δ ; (3) 求平均变化率的极限 0 0 0 0 0 ( )- ( ) ' | = lim = lim x x x x y f x x fx y x x = Δ→ Δ→ Δ + Δ Δ Δ . 例 1. 0 求函数 常数 在 点的导数 fx x ( )=C( ) . 解: 0 0 0 0 ( ) () - ( ) lim = =0 x fx x fx C C f x Δ → x x +Δ − ′ = Δ Δ . 即常数的导数为零. 例 2. 2 求函数 在点 的导数 fx x x ( )= 2 . = 解:给 x = 2一个增量Δx ,则函数增量为 22 2 Δ +Δ = Δ + Δ y=(2 ) -2 4 ( ) . x xx 平均变化 率为 =4+ , y x x Δ Δ Δ 于是 0 0 '(2) lim lim (4 ) 4. x x y f x Δ→ Δ→ x Δ = = +Δ = Δ 说明:如果函数 y = f x( ) 在区间(,) a b 内的每一点处都可导,则称函数 y = f x( ) 在 区间(,) a b 内可导,且称 f '( ) x 为函数 y = f x( ) 的导函数. 显然函数 y = f x( ) 在点 0 x 处的导数 0 f '( ) x ,就是导函数 f '( ) x 在 0 x 处的函数值,即 0 0 '( ) '( ) x x fx fx = = . 例 3.求函数 1 y= x 在 x=1处的导数. 解:先求导函数. 给任意一点 x 一个增量Δx ,得到 11 - = -= . + () x y x x x xx x Δ Δ Δ + Δ . 所以 2 0 0 -1 1 ' lim lim - . ( ) x x y y Δ→ Δ→ x xx x x Δ == = Δ +Δ 再求 x=1处的导数 =1 =1 2 1 ' ( - )| =-1. x x y x = 例 4. 求函数 y= x 的导数. 解:任取一点 x∈ ∞ (0,+ ) 一个增量Δx ,得到Δ Δ y=+- xx x - 1 == . + y x xx x x x x x Δ +Δ Δ Δ + Δ 所以 0 0 1 1 ' lim lim . + 2 x x y y x x xx x Δ→ Δ→ Δ == = Δ + Δ 说明:由前面的三个例子发现,幂函数的导数公式 -1 ( )' ( ) x x α α =α α为任一实数

同理,我们还可以证明 1 3、左导数与右导数 (1)求函数y=fx)在点x。处的导数时,x→x,的方式是任意的。如果x仅从x 之左趋于。,记作x→x,或△r→0,若此时y极限存在,则称该极限值叫 做函数)=在点气的左导数,记作∫-化,即了-(化广是同理有右 号数了,化)广册:,其中△→0广表示从x右侧趋于元 (2)函数在一点处的左、右导数与函数在该点处可导之间的关系 定理:函数y=f(x)在点x,可导的充分必要条件是函数y=(x)在点x,处的左 右导数存在且相等。 例:函数f(x)x在点x,=0处不可导. 解给气=0一个增量△0,则闲应的有左号数了-化广一是-一是= 同强,给6=0一个增量40,相应的右导数为八化广一是一会铝 即f(0)≠(0),故函数(x)x在点x=0处不可导. 三、函数的连续性与可导的关系 定理:如果函数y=f(x)在点x,处可导,那么y=f(x)在点x处连续. 该定理可可简术为:可导叫连续 说明:1.由可导的定义,变量、极限和无穷小量的关系定理可以证明 △r→0时,y=y'△r+ax→0 2.该定理的逆命题并不成立.如f(x)=x在点x,=0处连续但不可导. 四、高阶导数 因为y-f(x)的导函数f(x)也是x的导数,我们把函数y=f(x)的导数f'(x)的 导数(x)叫做函数的二阶导数,记作y,也可记作 减安其中空县密 二阶导数的力学意义是运动物体的加速度. 二阶导数的导数称为三阶导数。记作"《x)减 dx 设函数y=f(x)的存在n-1阶导数,且-1阶导数可导,那么y=f(x)的n-1阶
4 同理,我们还可以证明 1 1 (sin )' cos . (cos )' -sin . (log )' . (ln )' . ln a x xx x x x x a x = = == 3、左导数与右导数 (1)求函数 y fx = ( ) 在点 0 x 处的导数时, 0 x → x 的方式是任意的。如果 x 仅从 0 x 之左趋于 0 x ,记作 0 x → x -,或 - Δ →x 0 ,若此时 y x Δ Δ 极限存在,则称该极限值叫 做函数 y = f x( ) 在点 0 x 的左导数,记作 0 f ' _ ( ) x ,即 0 - 0 ' _ ( )= limx y f x Δ → x Δ Δ .同理有右 导数 + 0 + 0 ' ( )= limx y f x Δ → x Δ Δ ,其中 + Δ →x 0 表示从 0 x 右侧趋于 0 x . (2)函数在一点处的左、右导数与函数在该点处可导之间的关系 定理:函数 y fx = ( ) 在点 0 x 可导的充分必要条件是函数 y fx = ( ) 在点 0 x 处的左、 右导数存在且相等。 例:函数 f () | | x x = 在点 x0=0 处不可导. 解:给 x0=0 一个增量Δx0,相应的右导数为 + 0 + + 0 0 ' ( )= lim = lim =1. x x y x f x Δ→ Δ→ x x Δ Δ Δ Δ f f (0) (0), + − 即 ′ ′ ≠ 故函数 f () | | x x = 在点 x0=0 处不可导. 三、函数的连续性与可导的关系 定理:如果函数 y fx = ( ) 在点 0 x 处可导,那么 y fx = ( ) 在点 0 x 处连续. 该定理可简述为:可导则连续. 说明:1. 由可导的定义,变量、极限和无穷小量的关系定理可以证明 Δ →x 0时,Δyyx x = Δ+ Δ→ ' 0 α 2. 该定理的逆命题并不成立. 如 f () | | x x = 在点 x0=0 处连续但不可导. 四、高阶导数 因为 y = f x( ) 的导函数 f '( ) x 也是 x 的导数,我们把函数 y = f x( ) 的导数 f '( ) x 的 导数[ '( )]' f x 叫做函数的二阶导数,记作 y'' ,也可记作 2 2 2 2 ''( ) , = ( ). 或 其中 d y d y d dy f x dx dx dx dx 二阶导数的力学意义是运动物体的加速度. 二阶导数的导数称为三阶导数, 记作 3 3 '''= '''( ) . 或 d y yf x dx 设函数 y fx = ( ) 的存在 n-1 阶导数,且 n-1 阶导数可导,那么 y fx = ( ) 的 n-1 阶
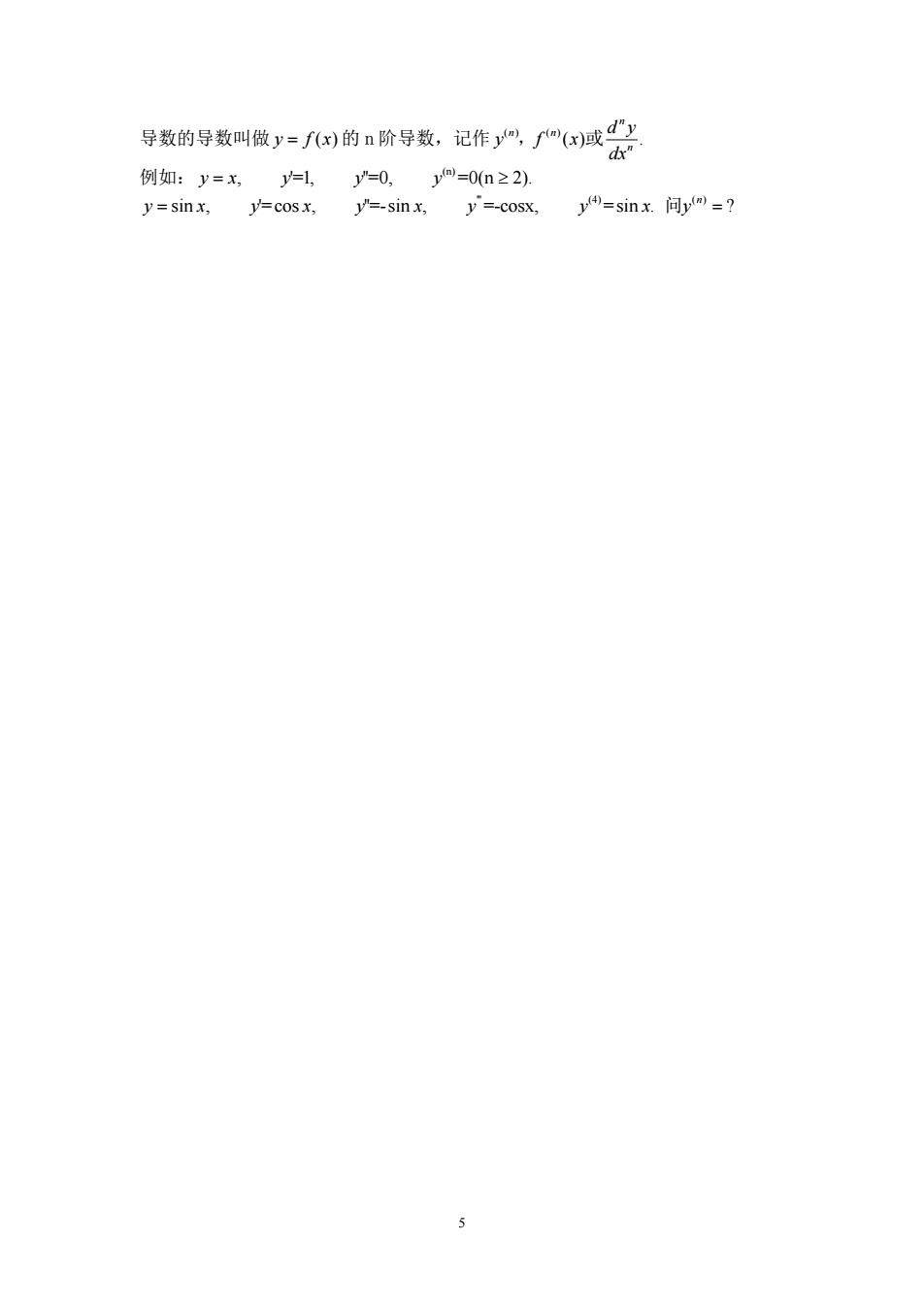
导数的导数叫做y=f)的n阶导数,记作%,了(x减以 例如:y=x,y=l,y=0,ym=0n≥2). y=sinx,y=cosx, y=-sinx,y'=-cosx y9=sinx.问ym=?
5 导数的导数叫做 y fx = ( ) 的 n 阶导数,记作 () () , 或 () . n n n n d y y fx dx 例如: (n) yx y y y = ≥ , '=1, ''=0, =0(n 2). ''' (4) ( ) sin , '= cos , ''=-sin , =-cosx, =sin . ? 问 n y x y x y x y y xy = =

第二节求导数的方法—法则与公式 般法则侧或公式呢? 一、 求导法则 因为初等函数是由基本初等函数经有限次四则运算和有限次复合而成,所以 先介绍函数的和、差、积、商及复合函数的求导法则. 1.函数和、差、积、商的求导法则 r-m2时o w2(x) 证明(1)设(x)和v(x)是x的可导函数.令y=(x)+(x).当x有增量△时, Ay=[(x+△r)+(x+△r-[u(x)+Wx】=[x+△r)(x)HHvx+△r)v(x)F△u+△v. 同理可得[u(xv(x)=(x(x) 证明(2)设(x)和(x)是x的可导函数.令y=(x)(x).当x有增量△x时, △y=[ux+△x)r(x+△xJ-[u(x)r(x】=[u(+△x)rx+△xi(x+△x)r(x】 +[u(r+△r)w(x-H(x)r(xF=u(x+△r)△v+(x)Au. y=是-倒尝+△点=0+x+A四 △ ='y+p'. 证明(3)略 说明:1. 空r-22Isr=grs3=得 例1己知y=x3-sinx+ln2,求y. :y=(x'-sinx+In2)'=(x'y'-(sinxY+(ln2)'=3x2-cosx. 例2己知y=x2nx+2 xcosx+π,求. 解:y'=(x2Inx+2 x COSx+πy=(x2lnxy+(2√c cosx)'+π' =(xYInx+x(Inx)'+(2)cosx+2(cosx) =2xlxxcos-2sinx. 例3.已知y=tanx,求. 解:y=(5y=6 sinx)cos-i (cas.xycos2x+sin2x。 1 cosx cos'x cos"x cos=seex. 6
6 第二节 求导数的方法——法则与公式 求变量的变化率—导数,是在理论研究和实践应用中经常遇到的一个普遍问 题,但根据定义求导数往往很繁难,有时甚至不可行,那么能否找到求导数的一 般法则或公式呢? 一、 求导法则 因为初等函数是由基本初等函数经有限次四则运算和有限次复合而成,所以 先介绍函数的和、差、积、商及复合函数的求导法则. 1. 函数和、差、积、商的求导法则 2 (1) [ ( ) ( )] ( ) ( ); (2) [ ( ) ( )] ( ) ( ) ( ) ( ); ( ) ( )( ) ( ) ( ) (3) [ ] ( ( ) 0). () () ux vx u x v x ux v x u xv x uxv x ux u xvx uxv x v x vx v x ± =± ′′ ′ ⋅= + ′′ ′ ′ ′ − ′ = ≠ 证明(1)设u x( ) 和v x( ) 是 x 的可导函数. 令 y ux vx x x = ( ) ( ). + Δ 当 有增量 时, Δ = +Δ + +Δ + = +Δ +Δ Δ +Δ y ux x vx x ux vx ux x ux vx x vx u v [ ( ) ( )]-[ ( ) ( )] [ ( )- ( )]+[ ( )- ( )]= . 00 00 ' lim lim[ ] lim lim ' '. xx xx y uv u v y u v Δ→ Δ→ Δ→ Δ→ x xx x x Δ ΔΔ Δ Δ = = + = + =+ Δ ΔΔ Δ Δ 同理可得[ ( )- ( )]'= '( )- '( ). ux vx u x v x 证明(2)设u x( ) 和v x( ) 是 x 的可导函数. 令 y uxvx x x = ( ) ( ). 当 有增量 时, Δ [ ( ) ( )]-[ ( ) ( )] [ ( ) ( )- ( ) ( )] +[ ( ) ( )- ( ) ( )]= ( ) ( ) . y ux xvx x uxvx ux xvx x ux xvx ux xvx uxvx ux x v vx u Δ = +Δ +Δ = +Δ +Δ +Δ +Δ +Δ Δ + Δ 00 00 0 ' lim lim[ ( ) ( ) ] ( ) lim lim ( ) lim ' '. xx xx x y uvu v y vx ux x vx ux x x xxx x uv vu Δ→ Δ→ Δ→ Δ→ Δ→ ΔΔ ΔΔ Δ = = + +Δ = + +Δ ΔΔΔΔ Δ = + 证明(3)略 说明: 1. 1 1 [ ( )] ( ); n n i i i i f x f x = = ∑ ∑ ′ ′ = 2. [ ( )] ( ); Cf x C ′ = f ′ x 3. 2 1 () [] . () () v x vx v x − ′ ′ = 例 1 已知 3 yx x =− + sin ln 2, 求 y'. 解: 3 yx x ′ ′ =− + ( sin ln 2) 3 2 = − + =− ( ) (sin ) (ln 2) 3 cos . x x xx ′ ′′ 例 2 已知 2 yx x x x =+ + ln 2 cos , π 求 y'. 解: 2 y xx x x ′ ′ =+ + ( ln 2 cos ) π 2 = ( ln ) (2 cos ) xx x x ′ + +′ ′ π 2 2 = ++ + ( ) ln (ln ) (2 ) cos 2 (cos ) x ′ ′′ ′ xx x x x x x cos 2 ln 2 sin . x x xx x x x = ++ − 例 3.已知 y = tan , x 求 y'. 解: 2 2 2 2 22 sin (sin ) cos sin (cos ) cos sin 1 ( ) sec . cos cos cos cos x x x xx x x y x x x xx ′ ′ − + ′ ′ = = = ==

例4.己知y=scx,求y cos'x cos2x cosx cosx 同理可得(cotx)/=-csc2x,(cscx/=-cscxcotx. 2.复合函数的求导法则 设p(x】是由函数y=f)及u=o(x)复合而成的函数,并设函数 u=p(x)在点x处可导,y=fu)在对应点u=p(x)处也可导,则有复合函数 Lpx川的求导法则: dydy du dx dud :也可表示为y'='4,'或y'=f()p() 说明:()若y=了,u=)v=(x)复合而成的函数)寸奶的中间变 量有两个以上的,则求导法则为 _少恤小或y,=y4 du dy dx (2)求复合函数的导数的关健,是对复合函数进行正确的分解 例5.求函数y=sin√的导数 解:令y=sin山wu=V.则y,'=y'4,'=(sin0)(V),'=cos 2√F2WF 例6.求函数y-Incos的导数. 解:令=ln山,u=cosy,=√.则 为'=男%',=hncs以'-sn 1 sin1_-tanv√F cos√2WF2Wx 例7.y=lnx小,求的导数 解:由定义域知y={-x0. 当x>0,y=hr-当r<0时yr=r=6= -x .a= 3.求隐函数的导数 如果方程F(x,y)=0确定了y是x的函数,那么,这样的函数叫做隐函数.设隐函 数y关于x可导,我们可以利用复合函数求导法则,求出隐函数y对x的导数. 例8方程x2-y+ny=0确定了y是x的隐函数,求. 解:因为y是x的隐函数,所以是y是x的复合函数.于是等式两端对x求导 数,有2x-广+=0.解得=2g y-1 例9.求由方程y-e+e=0所确定的隐函数y的导数y,以及y儿o 解:设由方程F(x,)=y-e+e'=0所确定了y=(x),对等式两端对x求导数有 (xy-(e'+(e=0',即y+y'e2+e'y'=0 7
7 例 4. 已知 y x = sec , 求 y'. 解: 2 1 (cos ) (sec ) ( ) cos cos x y x x x ′ ′′ ′ = = =− 2 sin 1 sin sec tan cos cos cos x x x x x xx = =⋅= . 同理可得 2 (cot ) csc , (csc ) csc cot x x x xx ′ ′ =− =− . 2. 复合函数的求导法则 设 y= [ ( )] f x ϕ 是由函数 y = f u( ) 及 u x =ϕ( ) 复合而成的函数,并设函数 u x =ϕ( ) 在点 x 处可导, y = f u( ) 在对应点u x =ϕ( ) 处也可导,则有复合函数 y= [ ( )] f x ϕ 的求导法则: = . dy dy du dx du dx 也可表示为 ' '' x u x y = y u 或 ' '( ) '( ). x y = fu x ϕ 说明:(1)若 y = == fu u v v x () () () , , ϕ ψ 复合而成的函数 y= { [ ( )]} f x ϕ ψ 的中间变 量有两个以上的,则求导法则为 = dy dy du dv dx du dv dx 或 ' ' ' '. x uvx y = yuv (2)求复合函数的导数的关键,是对复合函数进行正确的分解. 例 5. 求函数 的导数 y x = sin . 解: 令 y uu x =sin . , = 则 1 cos ' ' ' (sin ) '( ) '= cos = . 2 2 x ux u x x y yu u x u x x = = 例 6. 求函数 的导数 y x = ln cos . 解:令 y= ln cos = . uu vv x , , = 则 1 1 sin 1 - tan ' ' ' ' (ln ) '(cos ) '( ) ' (-sin ) - . 2 cos 2 2 x uvx u v x x x y yuv u v x v u x xx x == = = = 例 7. yxy = ln | | . ,求 的导数 解:由定义域知 ln 0, ln(- ) 0. x x y x x ⎧ > = ⎨ ⎩ = = < = == 时, 当 时, 1 (ln | |)' . x x ∴ = 3. 求隐函数的导数 如果方程 Fxy (, ) 0 = 确定了 y 是 x 的函数,那么,这样的函数叫做隐函数.设隐函 数 y 关于 x 可导,我们可以利用复合函数求导法则,求出隐函数 y 对 x 的导数. 例 8 方程 2 xy y −+ = ln 0 确定了 y 是 x 的隐函数,求 y'. 解:因为 y 是 x 的隐函数,所以是 lny 是 x 的复合函数. 于是等式两端对 x 求导 数,有2 0. y x y y ′ −+ = ′ 解得 2 . 1 xy y y ′ = − 例 9. - 0 x y 求由方程 所确定的隐函数 xy e e + = y 的导数 y',以及 0 '| . x y = 解:设由方程 ( , ) - + =0 x y F x y xy e e = 所确定了 y yx = ( ),对等式两端对 x 求导数有 '' ' ( ) - ( ) ( ) 0' '- ' 0 x y xy xx x xy e e y xy e e y + = + += ,即

轻又-隔-0儿 er+x 一 基本初等函数的求导公式 1.任意指数的幂函数=x“(aeR)的导数 对=r取对数,有lny=anr,其中lny是x复合函数.用复合函数求导法则可 得a子于是=a上述方法称为取对数法 2.指数函数y=a(a>0且a≠1)的导数 用取对数法,n=rna,两边对x求导,得兰=na,于是y'=yha=alna 特别地,a=e时,(e)'=e 3.反三角函数的导数 以反正弦商数为倒.设)户anxx1小Je(受则存在反函数x=m 对等式两端求x的导数,有1与yc0sy.由此得 1 cosy 1-sin2y v1-x2 同理可得((arccosx)'=- (arctanx)-(arecotx) 所以,基本初等函数的求导公式可由下表给出 (C)'=0 (x)'=axa-1 (Sinx) (cos.x)'=-sinx (tanx)=sec (cotx)'=-csc'x (secx)'=sec.xtan.x (cscx)=-cscxcotx (a')=a"ln (e")'=e* 1 (log.x)'= (arcsinx)'= V1-x2 (arccos.x)=- V1-x2 (arctanx)1+x (arccotx)=-1+x 例:求下列函数在指定点处的导数 f0=nsin,求牙: (2)/()=aresin+arctan). 解:)0=nny-m-=mt÷学=w4gl sintsint
8 =0 =0 =0 . 0 0 =1. x x y y x xy ey ey y xyy ex ex − − ∴ ′ ′ = == = + + 又 得, 二、 基本初等函数的求导公式 1.任意指数的幂函数 y=( ) x R α α ∈ 的导数 对 y=x α 取对数,有ln = ln y α x ,其中 lny 是 x 复合函数. 用复合函数求导法则可 得 -1 ' 1 = ' =. y y y x yx x α α α α ,于是 = 上述方法称为取对数法. 2. 指数函数 = ( >0 1) x ya a a 且 的导数 ≠ 用取对数法,ln = ln y x a ,两边对 x 求导,得 ' = ln ' ln = ln . y x a y y aa a y ,于是 = 特别地, = ( )' . x x ae e e 时, = 3. 反三角函数的导数 以反正弦函数为例, 设 = arcsin , (-1,1), (- , ). sin . 2 2 y xx y x y π π ∈∈ = 则存在反函数 对等式两端求 x 的导数,有1= 'cos y y . 由此得 2 2 11 1 '= = = cos 1-sin 1- y y y x . 同理可得 2 2 2 11 1 (arccos )' - , (arctan )' , ( cot )' - . 1- 1 1 x x arc x x x x = == + + 所以,基本初等函数的求导公式可由下表给出. 2 () 0 (sin ) cos (tan ) sec (sec ) sec tan C x x x x x xx ′ = ′ = ′ = ′ = 1 2 ( ) (cos ) sin (cot ) csc (csc ) csc cot x x x x x x x xx α α α − ′ = ′ = − ′ = − ′ = − ( ) ln 1 (log ) ln x x a a aa x x a ′ = ′ = ( ) 1 (ln| |) x x e e x x ′ = ′ = 2 2 1 (arcsin ) 1 1 (arctan ) 1 x x x x ′ = − ′ = + 2 2 1 (arccos ) 1 1 (arccot ) 1 x x x x ′ = − − ′ = − + 例:求下列函数在指定点处的导数. (1) ( ) lnsin , ( ); 4 ft t f π = 求 ′ 1 (2) ( ) arcsin arctan , (1). 2 t ft f t = + 求 ′ 解:(1) (sin ) cos ( ) (lnsin ) cot , sin sin t t f tt t t t ′ ′ ′ = = == 4 ( ) cot 1. 4 t f t π π = ∴ ′ = =

(2) ()=(arcsinarctany(aresin+(arctany -+ 4-Pr+1 11 11_25-3 f-气4-g26
9 (2) 1 1 ( ) (arcsin arctan ) (arcsin ) (arctan ) 2 2 t t f t t t ′ ′′′ =+ = + 2 2 2 1 2 1 1 , 4 1 1 1 1 2 t t t t t t ′ ′ ⎛⎞ ⎛⎞ ⎜⎟ ⎜⎟ ⎝⎠ ⎝⎠ = + =− ′ − + ⎛ ⎞ ⎛ ⎞ − + ⎜ ⎟ ⎜ ⎟ ⎝⎠ ⎝⎠ 2 2 1 1 1 1 1 23 3 (1) . 4 1 26 3 t f t t = ⎛ ⎞ − ∴ ′ = − = −= ⎜ ⎟ − + ⎝ ⎠

第三节局部改变量的估值问题一微分及其运算 一、 微分 1.引例:正方形金属薄片受热后面积的改变量。 设正方形边长由x,变到x,+△x,正方形面积A=x,2的改变量 △4=(x。+△r)2-x6=2x。·△r+(Ar)2. 2.定义:设函数y=f(x)在点x,处有增量△x,若相应的函数增量△y可表为 Ay=A△r+o(△,其中A与△r无关,A△r称为△y的线性主部,o(△r)是关 于△x的高阶无穷小量,则称函数y=f(x)在点x处可微,并称A△x为函数在点 x处的微分,记作或(x),即=df(x)=A△x.于是△y=+o(△r). 微分少叫做函数增量4y的线性主部. 说明:(1)△y是自变量的改变量△x的线性函数;(2)△y-=o(△x)是△x的 高阶无穷小:(3)A≠0山与Ay是等价无穷小:g=1+Ay→1(△r→) A△r (4)A是与△r无关的常数,但与fx)和c有关,A=f(x,) (⑤)△x=d(y=x→△r=yc=1=) 3.可微与可导之间的关系 由可微定义得4:一怎-了所以可微则可号:反过来,可号划可液所以 对于函数,求导数与求微分是一回事.即可微与可导等价. 二、徽分在近似计算中的应用 1.计算函数增量的近似值 若y=fx)在x的导数f'(x)≠0,且△很小时,4y≈四xf(x)△x 例:半径10厘米的金属圆片加热后半径伸长了0.05厘米,问面积增加多少? 解:设面积为A,由A=πr2,r=10厘米,△=0.05厘米 .△4≈d=2πr·△=2π×10×0.05=π(厘米2). 2.计算函数的近似值 求fx)在x=x,附近的近似值;由△y=fx,+△x)-fx)≈f'(x)△x可求得 f(x。+△r)≈f(x)+f'(x)△r. 例:计算下列各数的近似值985 解fx)=,98.5=1000-1.5≈f1000)+f'(1000)(1.5) =100+00035)=10-了×102×15=9.95
10 第三节 局部改变量的估值问题——微分及其运算 一、 微分 1. 引例:正方形金属薄片受热后面积的改变量. 设正方形边长由 0 x 变 到 0 x x + Δ ,正方形面积 2 A 0 = x 的改变量 2 2 0 0 Δ = +Δ − A ( ) x xx 2 0 = ⋅Δ + Δ 2 ( ). xx x 2. 定义:设函数 y f = ( ) x 在点 0 x 处有增量 Δx ,若相应的函数增量 Δy 可表为 Δ= Δ+ Δ y Ax x ο( ), 其中 A 与Δx 无关, AΔx 称为Δy 的线性主部, ο( ) Δx 是关 于Δx 的高阶无穷小量,则称函数 y f = ( ) x 在点 x 处可微,并称 AΔx 为函数在点 x 处的微分,记作dy df x 或 ( ) ,即dy = df () . x Ax = Δ 于是Δy = +Δ dy ο( ). x 微分 dy 叫做函数增量Δy 的线性主部. 说明:(1)Δy 是自变量的改变量Δx 的线性函数; (2)Δy − =Δ dy o x ( )是Δx 的 高阶无穷小;(3) A ≠ 0 dy y 与Δ 是等价无穷小; y dy Δ ( ) 1 10 o x x A x Δ =+ → Δ→ ⋅ Δ ( ). (4) A是与Δx 无关的常数,但与 0 f ( ) x x 和 有关, ' 0 A f = ( ) x (5) ' Δ = = ⇒Δ = = ⋅ = x dx( ) y x x y dx dx dx 1 3. 可微与可导之间的关系 由可微定义得 0 lim ( ). x y A f x Δ → x Δ = = ′ Δ 所以可微则可导;反过来,可导则可微. 所以 对于函数,求导数与求微分是一回事. 即可微与可导等价. 二、 微分在近似计算中的应用 1. 计算函数增量的近似值 若 0 y f = ( ) x x 在 的导数 0 f ′( ) 0, x x ≠ 且 Δ 很小时, 0 0 xx xx = '( ) 0 y dy f x x Δ = = ≈ Δ 例:半径 10 厘米的金属圆片加热后半径伸长了 0.05 厘米,问面积增加多少? 解:设面积为 A,由 2 A = π r , r r = 10 , 0.05 . 厘米 厘米 Δ = ∴ Δ ≈ = ⋅Δ A d rr 2π = ×× 2 10 0.05 π 2 = π ( ). 厘米 2. 计算函数的近似值 0 求 在 附近的近似值 由 fx x x () ; = 0 00 Δy f = +Δ − ≈ Δ ( ) ( ) '( ) x x f x f x x 可求得 0 00 f ( ) () () . x x +Δ ≈ + ⋅Δ f x f ′ x x 例:计算下列各数的近似值 3 998.5 解 33 3 fx x ( ) , 998.5 1000 1.5 = =− ≈ f f (1000) '(1000)(-1.5) + 2 - 3 3 1 = 1000+ (1000) (-1.5) 3 × 1 -2 =10 10 1.5 3 −× × = 9.995. = 0.97