第四章导数的应用问题 4.1中值定理 4.2洛必达法则 4.3函数的单调性与极值
第四章 导数的应用问题 4.1 中值定理 4.2 洛必达法则 4.3 函数的单调性与极值

4.1中值定理 一.费马定理 皮埃尔·德·费马(Fermat),法国 律师和业余数学家。他对数论最有兴 趣,亦对现代微积分的建立有所贡献。 费马在笛卡尔《几何学》发表 之前,就于1629年发现了解析几何 的基本原理,建立了坐标法,是解析 几何的发明人之一,同年写了《求最 大最小值的方法》。 费马善于思考,特别善于猜想, 费马(1601-1665) 提出了数论中的许多猜想,人们也称 费马是“猜想数学家”。 x”+y”=z
4.1 中值定理 一. 费马定理 费马在笛卡尔《几何学》发表 之前,就于1629年发现了解析几何 的基本原理,建立了坐标法,是解析 几何的发明人之一,同年写了《求最 大最小值的方法》。 费马善于思考,特别善于猜想, 费马 (1601-1665) 提出了数论中的许多猜想,人们也称 费马是“猜想数学家”。 皮埃尔·德·费马(Fermat),法国 律师和业余数学家。他对数论最有兴 趣,亦对现代微积分的建立有所贡献。 n n n x y z + =
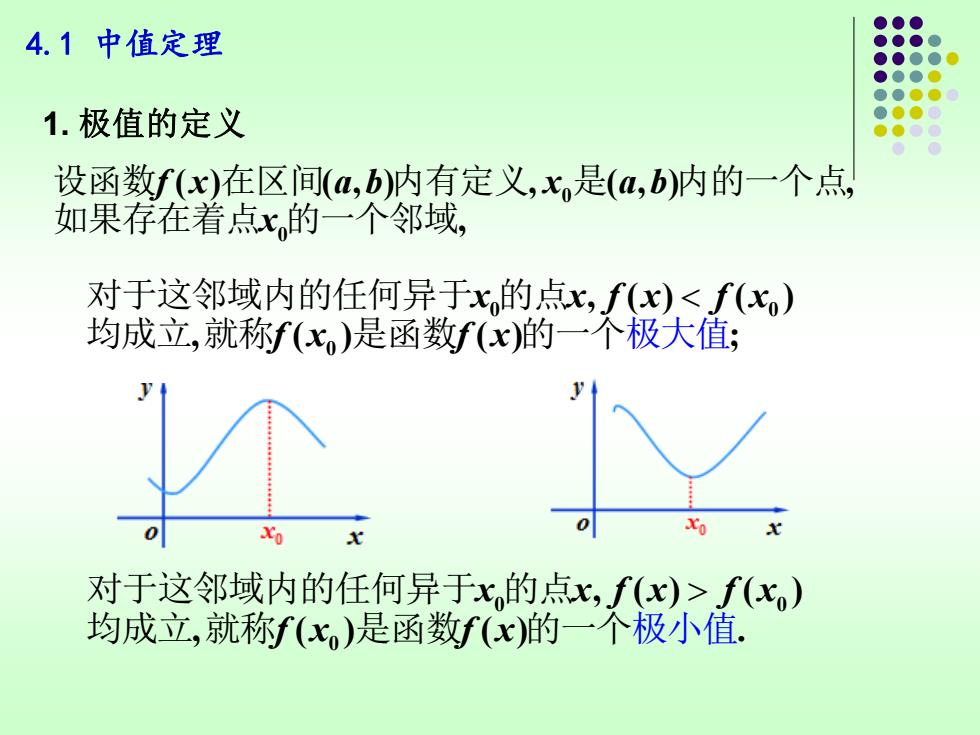
4.1中值定理 1.极值的定义 设函数f(x)在区间(a,b)内有定义,x,是(a,b)内的一个点, 如果存在着点x的一个邻域, 对于这邻域内的任何异于x的点飞,f(x)f(x) 均成立,就称f(x)是函数f(x)的一个极小值
4.1 中值定理 0 0 ( ) ( , ) , ( , ) , , f x a b x a b x 设函数 在区间 内有定义 是 内的一个点 如果存在着点 的一个邻域 0 0 0 , ( ) ( ) , ( ) ( ) ; x x f x f x f x f x 对于这邻域内的任何异于 的点 均成立 就称 是函数 的一个极大值 0 0 0 , ( ) ( ) , ( ) ( ) . x x f x f x f x f x 对于这邻域内的任何异于 的点 均成立 就称 是函数 的一个极小值 1. 极值的定义
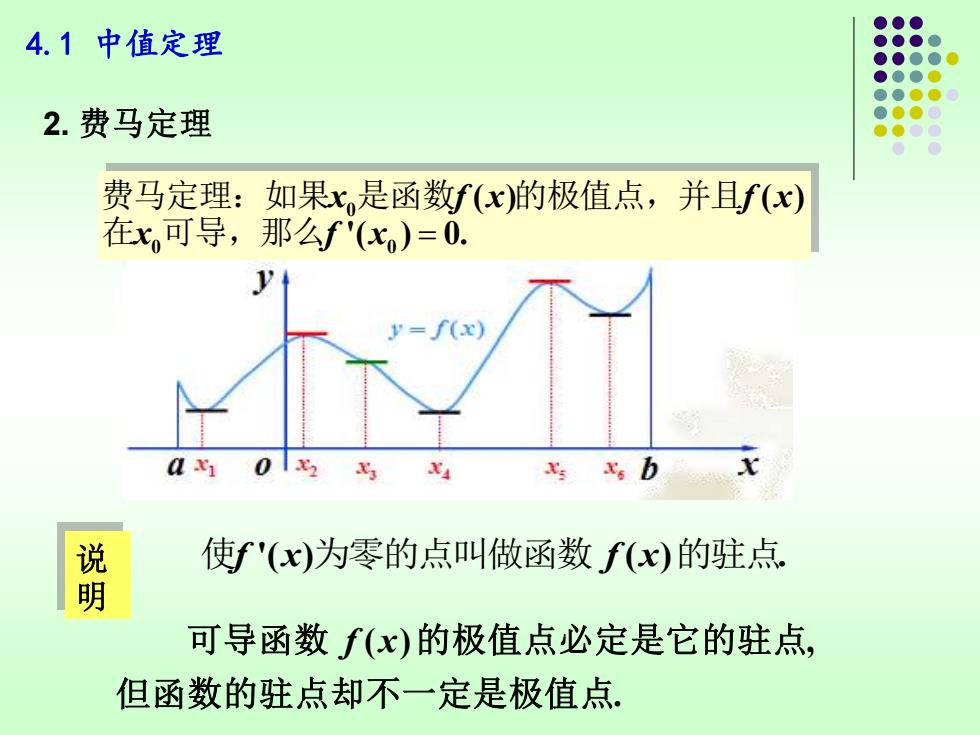
4.1中值定理 2.费马定理 费马定理:如果x,是函数f(x)的极值点,并且f(x) 在x可导,那么f'(x)=0. y=f(x) 01 使f'(x)为零的点叫做函数f(x)的驻点. 明 可导函数f(x)的极值点必定是它的驻点, 但函数的驻点却不一定是极值点
4.1 中值定理 0 0 0 ( ) ( ) '( ) 0. x f x f x x f x = 费马定理:如果 是函数 的极值点,并且 在 可导,那么 2. 费马定理 使f x f x '( ) ( ) . 为零的点叫做函数 的驻点 . ( ) , 但函数的驻点却不一定是极值点 可导函数 f x 的极值点必定是它的驻点 说 明
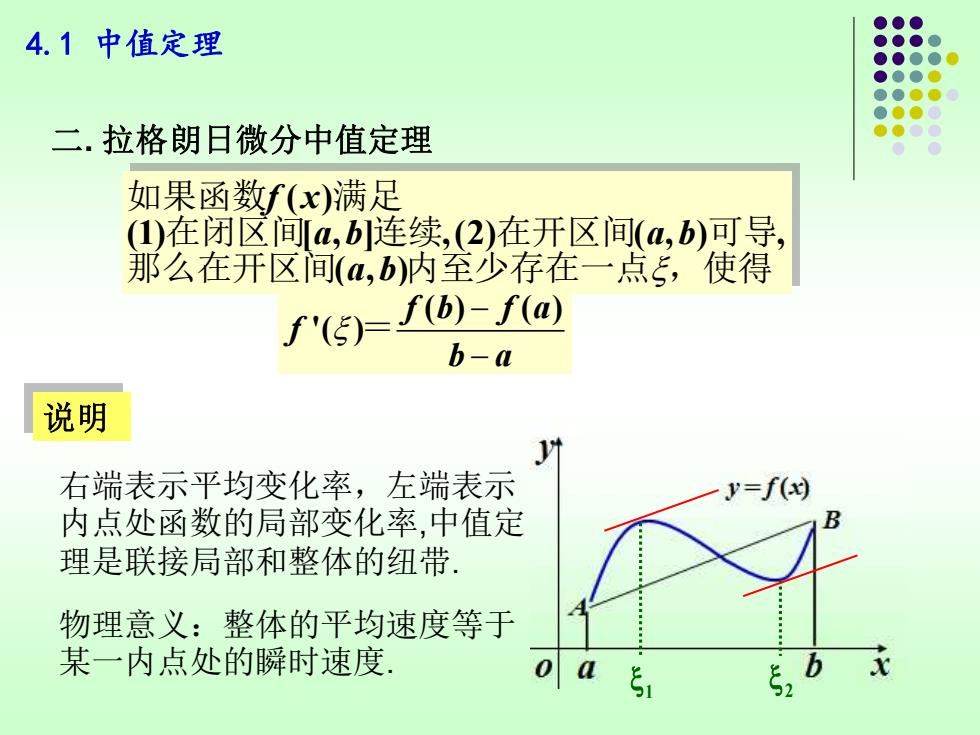
4.1中值定理 二.拉格朗日微分中值定理 如果函数f(x)满足 (1)在闭区间4,b连续,(2)在开区间(a,b)可导, 那么在开区间(a,b)内至少存在一点5,使得 f'(5)=f)-fa b-a 说明 右端表示平均变化率,左端表示 y=f(9 内点处函数的局部变化率,中值定 理是联接局部和整体的纽带 物理意义:整体的平均速度等于 某一内点处的瞬时速度 ¥bx
1 2 4.1 中值定理 二. 拉格朗日微分中值定理 ( ) (1) [ , ] , (2) ( , ) , ( , ) f x a b a b a b 如果函数 满足 在闭区间 连续 在开区间 可导 那么在开区间 内至少存在一点 ,使得 ( ) ( ) '( ) f b f a f b a − − = 说明 右端表示平均变化率,左端表示 内点处函数的局部变化率,中值定 理是联接局部和整体的纽带. 物理意义:整体的平均速度等于 某一内点处的瞬时速度

若f(x)在a,b]连续,f(x)在(a,b)可导, 4.1中值定理 则归5∈(a,b)f'5)=f@)-f6 a-b 推论1 若f(x)在(,b)导数恒为零,则f(x)是(a,b)内的常数函数 即f'(x)≡0台f(x)=C(C为常数) 推论2 若f(x)和g(x)在(a,b)内可导,且f'(x)≡g'(x), 则它们至多相差一个常数,即 f(x)=g(x)+C(C为常数)
4.1 中值定理 推论1 若f x a b f x a b ( ) ( , ) , ( ) ( , ) 在 导数恒为零 则 是 内的常数函数. ( ) [ , ] , ( ) ( , ) , ( ) ( ) ( , ) '( ) . f x a b f x a b f a f b a b f a b − − 若 在 连续 在 可导 则 , = 即f x f x C C '( ) 0 ( ) = ( 为常数) 推论2 C ( ) ( ) ( , ) , '( ) '( ), ( ) ( ) ( ). f x g x a b f x g x f x g x C = + 若 和 在 内可导 且 则它们至多相差一个常数,即 为常数

4.1中值定理 罗尔定理 拉格朗日定理的特例 若f(x)在a,b连续,f(x)在(@,b)可导, y=f(x) 且f()=fb),则至少存在一点 5∈(a,b),使得 f'(5)=0 0 E2 b 若罗尔定理的三个条件中有一个不满足,其结论可能不成立 柯西定理 一拉格朗日定理的推广 如果函数f(x)和g(x)在a,b连续,在(a,b)可导, 且g'(x)≠0,则在(a,b)内至少存在一点5,使得 f(b)-f(a)_f'(5) g(b)-g(a)g'(5) g()=x时,即得拉格朗日中值定理
4.1 中值定理 柯西定理 ——拉格朗日定理的推广 ( ) ( ) [ , ] ( , ) , '( ) 0, ( , ) f x g x a b a b g x a b 如果函数 和 在 连续,在 可导 且 则在 内至少存在一点 ,使得 ( ) ( ) '( ) . ( ) ( ) '( ) f b f a f g b g a g − − = g x x ( ) . = 时,即得拉格朗日中值定理 ( ) [ , ] , ( ) ( , ) , ( ) ( ), ( , ) '( ) 0 f x a b f x a b f a f b a b f = 若 在 连续 在 可导 且 则至少存在一点 ,使得 = 罗尔定理 ——拉格朗日定理的特例 若罗尔定理的三个条件中有一个不满足,其结论可能不成立

4.1中值定理 数学家简介一 约瑟夫·拉格朗日 Lagrange,1736~1813 法国数学家,在力学和天文学的领域中 也都有历史性的贡献,其中尤以数学方面 的成就最为突出。 他最突出的贡献是在把数学分析的基础 脱离几何与力学方面起了决定性的作用, 使数学的独立性更为清楚,而不仅是其他 学科的工具。同时在使天文学力学化、力 学分析化上也起了历史性作用,促使力学 和天文学(天体力学)更深入发展。 他在数学史上被认为是对分析数学的发展产生全面影响的 数学家之一
4.1 中值定理 约瑟夫·拉格朗日 法国数学家,在力学和天文学的领域中 也都有历史性的贡献,其中尤以数学方面 的成就最为突出。 他最突出的贡献是在把数学分析的基础 脱离几何与力学方面起了决定性的作用, 使数学的独立性更为清楚,而不仅是其他 学科的工具。同时在使天文学力学化、力 学分析化上也起了历史性作用,促使力学 和天文学(天体力学)更深入发展。 Lagrange,1736~1813 他在数学史上被认为是对分析数学的发展产生全面影响的 数学家之一。 数学家简介一

4.1中值定理 数学家简介二 柯西(Cauchy,1789一1857)是法国数 学家,天文学家,物理学家。柯西在 微积分历史上的影响尤其深远。他提出 极限定义的方法(当今所有微积分的教 科书都还沿用着柯西等人关于极限、连 续、导数、收敛等概念的定义);他 利用中值定理首先严格证明了微积分基 本定理.他还在代数方面、理论物理 光学等方面有突出贡献。 正是通过柯西以及后来魏尔斯特拉斯的艰苦工作,使数学分 析的基本概念得到严格的论述。从而结束微积分二百年来思 想上的混乱局面
4.1 中值定理 柯西(Cauchy, 1789—1857)是法国数 学家, 天文学家,物理学家。柯西在 微积分历史上的影响尤其深远。他提出 极限定义的方法(当今所有微积分的教 科书都还沿用着柯西等人关于极限、连 续、导数、收敛等概念的定义 );他 利用中值定理首先严格证明了微积分基 本定理.他还在代数方面、理论物理、 光学等方面有突出贡献。 正是通过柯西以及后来魏尔斯特拉斯的艰苦工作,使数学分 析的基本概念得到严格的论述。从而结束微积分二百年来思 想上的混乱局面。 数学家简介二

思考与练习 1.什么是函数的极值?什么是函数的最值? 两者有什么关系? 2.费马定理和函数的极值有什么关系? 3.中值定理的假设和结论是什么?如果没 有定理的假设,结论能否成立?
思考与练习 1.什么是函数的极值?什么是函数的最值? 两者有什么关系? 2.费马定理和函数的极值有什么关系? 3.中值定理的假设和结论是什么?如果没 有定理的假设,结论能否成立?