
第六章定积分及其应用 6.1定积分的概念及性质 6.2定积分的计算方法 6.3非正常积分 6.4定积分的应用
第六章 定积分及其应用 6.1 定积分的概念及性质 6.2 定积分的计算方法 6.3 非正常积分 6.4 定积分的应用

6.2定积分的计算方法 回顾:定积分的概念 ∫2fx)dx=im∑f5)△x,· d→0 i=1 ·用定积分的定义直接去求积分和的极限是十分困难的。 。 不定积分和定积分是两个完全干的概念,但是牛顿和 莱布尼茨发现这两个不同概念之间存在着深刻的内在 联系,即所谓的微积分基本定理, ·由此开辟的求定积分的新途径一牛顿莱布尼茨公式, 使积分学和微分学一起构成变量数学的基础学科一一 微积分学
6.2 定积分的计算方法 ⚫ 用定积分的定义直接去求积分和的极限是十分困难的。 ⚫ 不定积分和定积分是两个完全干的概念,但是牛顿和 莱布尼茨发现这两个不同概念之间存在着深刻的内在 联系,即所谓的微积分基本定理, ⚫ 由此开辟的求定积分的新途径——牛顿-莱布尼茨公式, 使积分学和微分学一起构成变量数学的基础学科—— 微积分学. 回顾:定积分的概念 ( ) d lim ( ) . 1 0 = → = n i i i d b a f x x f ξ x
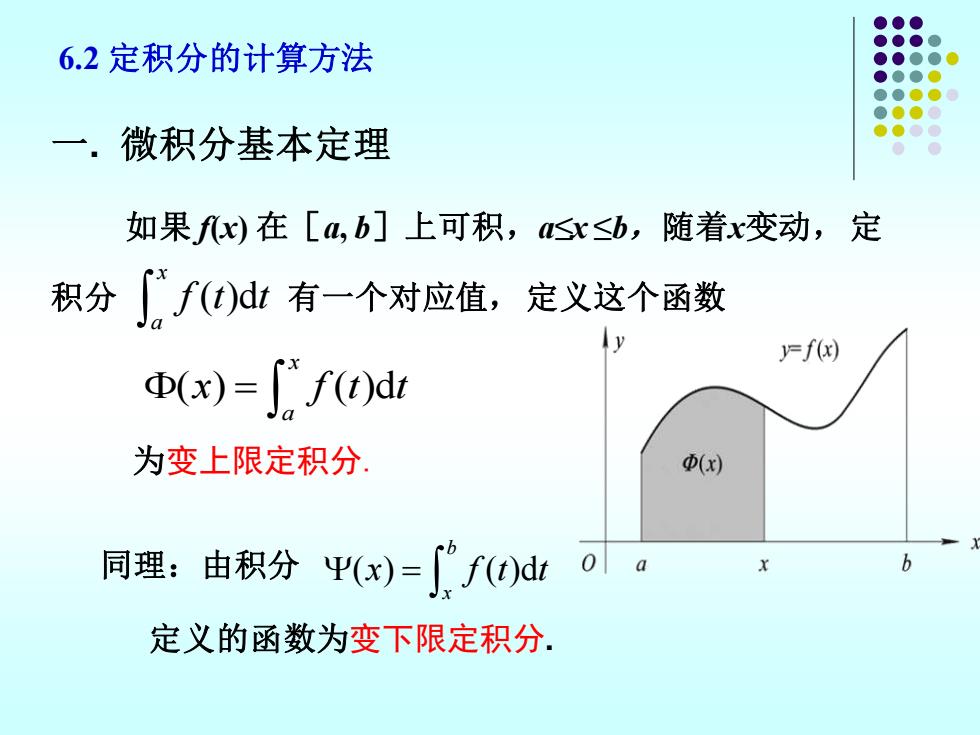
6.2定积分的计算方法 一.微积分基本定理 如果fx)在[4,b]上可积,sx≤b,随着x变动,定 积分f()dt有一个对应值,定义这个函数 Ff树 (x)=["f()di 为变上限定积分 (x) 同理:由积分平(x)=心f)dtoa b 定义的函数为变下限定积分:
6.2 定积分的计算方法 一. 微积分基本定理 如果 f(x) 在[a, b]上可积,a≤x ≤b,随着x变动,定 积分 ( )d 有一个对应值,定义这个函数 x a f t t ( ) ( )d x a = x f t t 为变上限定积分. ( ) ( )d b x = x f t t 同理:由积分 定义的函数为变下限定积分

6.2定积分的计算方法 定理1如果fx)在[a,b]上连续,则变上限积分函数 Φ(x)=fu 在[a,1]上可导,且D'(x)=f(x)(a≤≤b) 即Φ(x)是被积函数f(x)在a,b]上的一个原函数,并且 ①D(x)在[a,b]上连续
6.2 定积分的计算方法 定理 1 如果f(x)在[a, b]上连续,则变上限积分函数 x f t t x a ( ) ( )d = 在 [a, b] 上可导,且 = ( ) ( ) x f x (a≤x≤b) ( ) ( ) [ , ] ( ) [ , ] . x f x a b x a b 即 是被积函数 在 上的一个原函数,并且 在 上连续

6.2定积分的计算方法 Φ'(x)=f(x) 定理1的证明 证 这里要求Φx)的导数,我们就按照导数的定义来求 解.(x)在x+x处的函数值为 (x+Ax)=f(Xlr 由此得函数的增量 △D=Φ(x+Ax)-Φ(x)=fuh-fud -f+f-ffd =∫“f0)d
6.2 定积分的计算方法 证 这里要求Φ(x)的导数,我们就按照导数的定义来求 解. Φ(x)在x+Δx处的函数值为 Φ x x f t t x x a ( ) ( )d + + = 由此得函数的增量 = ( ) ( ) x f x 定理1的证明 = (x + x) −(x) f t dt f t dt x a x x a = − + ( ) ( ) f t dt f t dt f t dt x a x x x x a = + − + ( ) ( ) ( ) ( ) x x x f t dt + =

6.2定积分的计算方法 △Φ=x+△x)-()=t“f)dl 由积分中值定理得 ∫fxc=f(传b-a) △Φ=f(5)△x,5∈[x,x+△x] 2=f) 当△x→0时,即x,所以 △Φ lim =imf(传)=f(x) Ax→0△x △x0 故Φ'(x)=f(x)
6.2 定积分的计算方法 由积分中值定理得 = f x ( ) , + [ , ] x x x = (x + x) −(x) ( ) x x x f t dt + = f ( ) x = 当Δx→0时, 即ξ→x, 所以 lim lim ( ) ( ) 0 0 f f x x Φ x x = = → → 故 = '( ) ( ). x f x ( )d ( )( ) b a f x x f b a = −

6.2定积分的计算方法 定理2(牛顿莱布尼茨公式) 如果函数Fx)是连续函 数fx)在区间[4,b]上的一个原函数,则 f(=F(b)-F(a) 该公式也常记作∫f(x)=F(x)白=F(b)-F(a) 牛顿-莱布尼茨公式将定积分的计算转化为求一个原函数在 上下限之差的问题,将定积分和不定积分巧妙的联系起来
6.2 定积分的计算方法 定理2(牛顿-莱布尼茨公式) 如果函数F(x)是连续函 数 f(x) 在区间[a, b]上的一个原函数,则 f (x)dx F(b) F(a) b a = − ( ) ( ) | ( ) ( ) b b a a f x dx F x F b F a = = − 该公式也常记作 牛顿-莱布尼茨公式将定积分的计算转化为求一个原函数在 上下限之差的问题,将定积分和不定积分巧妙的联系起来

6.2定积分的计算方法 定理2的证明 已知函数Fx)是x)的一个原函数,D(x)=f 也是孔x)的一个原函数.于是F(x)与D(x)只相差一个常数, 即F(x)-Φx)=C,x∈[a,b] 在上式中令a,得a)-a-C因为a)-fe=0 得Fa-C.因为F()-∫ft=C 在上式中令xb,得∫fx=F(b)-F(a)
6.2 定积分的计算方法 Φ x f t t x a ( ) ( )d = 也是 f(x) 的一个原函数. 于是F(x)与Φ(x)只相差一个常数, 即 F(x)-Φ(x)=C, x∈[a, b] 定理2的证明 已知函数F(x)是f(x)的一个原函数, 在上式中令x=a, 得F(a)-Φ(a)=C. 因为 ( ) = ( )d = 0 Φ a f t t a a 得F(a)=C. 因为 ( ) ( )d x a F x f t t C − = 在上式中令x=b, 得 ( ) ( ) ( ) b a f x dx F b F a = −

6.2定积分的计算方法 [f(x)dx=F(b)-F(a) 例题1 计算:rd 谣了=写 = 3/I 3 例题2 计算:反sin. 解 [sin xdx=-cosx2-cos+cos0=1
6.2 定积分的计算方法 ( ) ( ) ( ) b a f x dx F b F a = − 例题1 1 2 0 x dx 计算: 解: C x x dx = + 3 3 2 1 0 3 1 0 2 3 x x dx = 3 1 = 2 0 sin xdx 例题 计算: 2 解: 2 / 2 0 0 sin cos | cos cos0 1. 2 xdx x = − = − + =

6.2定积分的计算方法 三.定积分的换元积分法和分部积分法 定理3(定积分的换元法)若fx)在[4,b]上连续;满足 (1)函数x=p()在[a,B]上是单值的且有连续导数; (2)当在区间[a,B]上变化时,=p()的值在[a,b] 上变化,且p(a=、p()=b,则有 Ifh-neeout
6.2 定积分的计算方法 定理3(定积分的换元法) 若 f(x)在[a, b]上连续;满足 (1) 函数x=φ(t)在[α, β]上是单值的且有连续导数; (2) 当t在区间[α, β]上变化时,x=φ(t)的值在[a, b] 上变化, 且φ(α)=a、 φ(β)=b, 则有 三. 定积分的换元积分法和分部积分法 f x dx f t t t b a ( ) [ ( )] ( )d =