
第三节函数的极限 一、x→oo时,函数f(x)的极限 二、x→+o时,函数f(x)的极限 三、x→-o∞时,函数f(x)的极限 四、x→x时,函数f(x)的极限 x→x+0(x→x)时,函数f(x)的极限 x→x-0(x→x)时,函数f(x)的极限 小结与思考
第三节 函数的极限 一、x →时,函数 f (x)的极限 二、x →+时,函数 f (x)的极限 五、x → x + 0 (x → x0 + )时,函数 f (x)的极限 六、x → x − 0 ( x → x0 − )时,函数 f (x)的极限 三、x →−时,函数 f (x)的极限 四、x → x0 时,函数 f (x)的极限 七、小结与思考

、当x>0时函数的极限 y 考察当x→∞时,函数f(x)=二 的变化趋势 X 1 由图可以看出,当X的绝对值无限增大时, y= X f(x)1 的值无限接近零。 1 →0, X→十00 X x 1 >0, X→-∞ X 1 即:二→0, X→00 X 小作米 ✉合
一、当 x → 时函数的极限 x y 1 = x y O 考察当 x → 时,函数 的变化趋势 x f x 1 ( ) = 0, x → + 1 → x x f (x) 由图可以看出,当 的绝对值无限增大时, 的值无限接近零。 即: 0, x →- 1 → x 0, x → 1 → x

定义1如果当X的绝对值无限增大(即x→∞) 时,函数f(x)无限接近于一个确定的常数A,那么常 数A就叫函数f(x)当x→o时的极限,记作 Iimf(x)=A或f(x)→A(当x→oo) 上述例子可以记为mmf()=m1=0 >00 X→0X
定义 1 如果当 x 的绝对值无限增大(即 x → ) 时,函数 f (x)无限接近于一个确定的常数A,那么常 数A就叫函数 f (x)当x → 时的极限,记作 lim ( ) = ( ) → ( → ) → f x A f x A x x 或 当 0 1 lim ( ) = lim = → → x f x x x 上述例子可以记为

定义2 如果当x→+0时,函数f(x)无限接近于一 个确定的常数A,那么常数A就叫函数f(x)当x→+∞时 的极限,记作 limf(x)=A或记为,f(x)→A(x→+o) x→+00 米吃 ✉合
定义 2 如果当 x → + 时,函数 f (x)无限接近于一 个确定的常数A,那么常数A就叫函数 f (x)当 x → +时 的极限,记作 = 或记为, → ( → +) →+ f x A f x A x x lim ( ) ( )
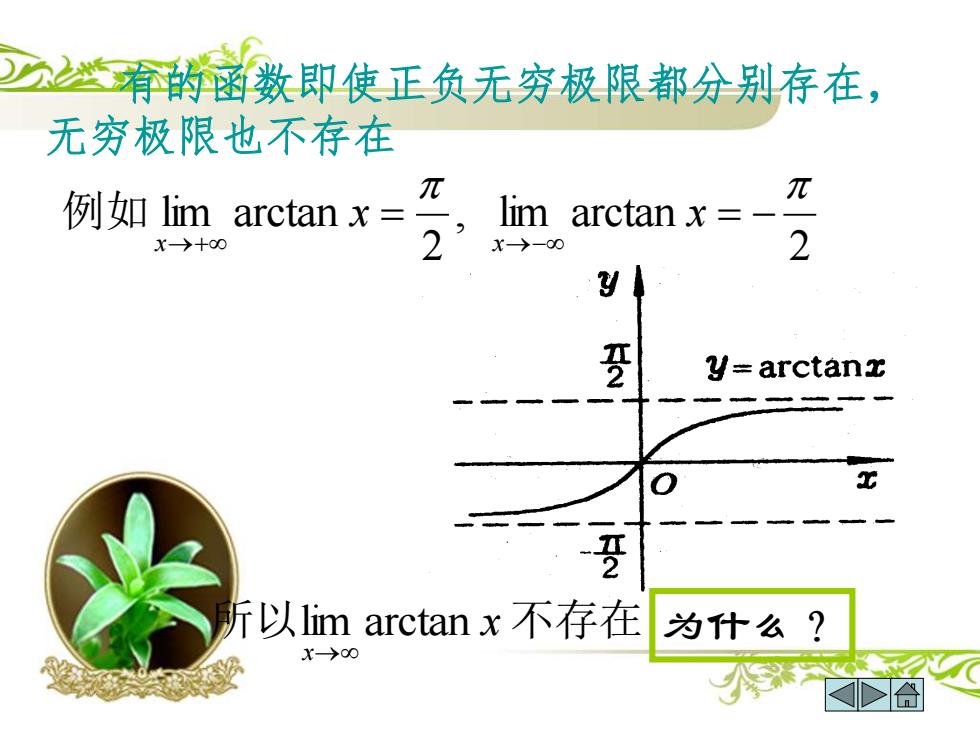
有的函数即使正负无穷极限都分别存在, 无穷极限也不存在 例如lim arctan x= π 元,lim arctan x= π X>+00 2 X>-00 2 罗 y=arctanz 斤以lim arctanx不存在 为什么? X→00 合
, 2 lim arctan = →+ x x 例如 所以 x 不存在 x lim arctan → 为什么? 有的函数即使正负无穷极限都分别存在, 无穷极限也不存在 2 lim arctan = − →− x x

般地,mf(x)=A的充分必要条件是 >00 im f(x)=lim f(x)=4 y 例1求lime*和lim ex X>-0∞ X→+o0 y=arccotx 解 lim e*=0,lim e*=0. X-→-00 x>+00 例2 沦当x→oo时,函数y=arc cotx的极限 解】 因为m arccotx=0,lim arccotx=π m arc cot x不存在 x0
f x A x = → lim ( ) f x f x A x x = = →+ →− lim ( ) lim ( ) 一般地, 的充分必要条件是 . 例1 x x x x e e − →− →+ 求 lim 和 lim lim = 0, lim = 0. − →− →+ x x x x 解 e e 例2 讨论当x →时,函数y = arccot x的极限. 解 = = →+ →− arc x arc x x x 因为 lim cot 0, lim cot 所以lim arc cot x不存在. x→

二、当x)x时函数的极限 定义3如果当X无限接近于定值x0,即x→x。 (x可以不等于xo)时,函数f(x)无限接近于一 个确定的常数A,那末A就叫函数f(x)当x→x, 时的极限,记作 limf(x)=A或f(x)→A(当x→,) x→x0 注意 义中,"x→x,"表示以任意方式趋近于x。 2函数极限 与f(x)在点x是否有定义无关。 米 合
定义 3 如果当 x 无限接近于定值 0 x ,即 x → x0 ( x 可以不等于 0 x )时,函数 f (x)无限接近于一 个确定的常数A,那末A就叫函数 f (x)当x → x0 时的极限,记作 lim ( ) ( ) ( ) 0 0 f x A f x A x x x x = → → → 或 当 二、当 x → x0 时函数的极限 注意: 0 0 1.在上面定义中,"x → x "表示以任意方式趋近于x 2.函数极限与f (x)在点x0 是否有定义无关

例考察极限limC(C为常数). lim x2. x→x0 x-→2 解: lim C=C x→x0 limx2=22=4. rs? 米 ✉合
例 考察极限 lim . 2 2 x x→ 解: lim 2 4. 2 2 2 = = → x x lim ( ). 0 C C为常数 x→x C C x x = → 0 lim
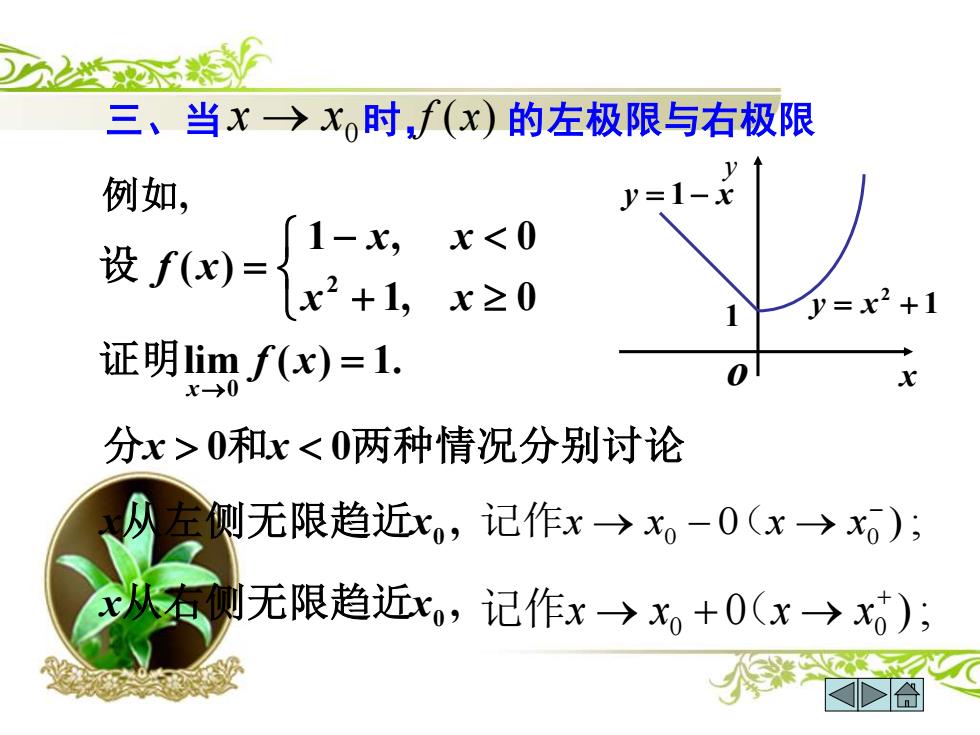
三、当x→xo时,f(x)的左极限与右极限 例如, y=1-x 设f(x)= 1-x,x0和x<0两种情况分别讨论 左侧无限趋近xo,记作x→x。-0(x→x); 右侧无限趋近xo,记作x→x+0(x→x); 作米 合
三、当 时, 的左极限与右极限 例如 , lim ( ) 1.1, 0 1 , 0 ( )0 2= + − = → f xx x x x f xx 证明设分x 0和x 0两种情况分别讨论 , x从左侧无限趋近x0 0 ) ; 0 0 → − 记作 x → x − ( x x , x从右侧无限趋近x0 0 ) ; 0 0 → + 记作 x → x + ( x x yo x 1 y = 1 − x 1 2 y = x + 0 x → x f (x)

定义4如果当x→x。-时,函数f(x)无限接近于 一个确定的常数A,那末A就叫函数f(x)当 x→x时的左极限, 记作Iim.f(x)=A或f(x-0)=A. x→x0-0 (x→x0) 右极限 lim f(x)=A f(x+0)=A. 0+0 o) 米
左极限 右极限 lim ( ) ( 0) . 0 ( ) 0 0 0 f x A f x A x x x x = − = → − → − 记作 或 lim ( ) ( 0) . 0 ( ) 0 0 0 f x A f x A x x x x = + = → + → + 记作 或 定义 4 如果当 0 x → x -时,函数 f ( x)无限接近于 一个确定的常数A,那末A就叫函数 f (x)当 0 x → x 时的左极限