
第2章 布尔代数基础 2.1逻辑代数基础 2.1.1逻辑代数的基本概念 2.1.2 逻辑函数 2.1.3 逻辑代数的公理、定理和规则 2.1.4逻辑表达式的基本形式 2.1.5逻辑函数的标准形式 2.1.6逻辑函数表达式的转换 2.2逻辑函数的化简 2.2.1代数化简法 2.2.2卡诺图化简法
第2章 布尔代数基础 2.1 逻辑代数基础 2.1.1 逻辑代数的基本概念 2.1.2 逻辑函数 2.1.3 逻辑代数的公理、定理和规则 2.1.4 逻辑表达式的基本形式 2.1.5 逻辑函数的标准形式 2.1.6 逻辑函数表达式的转换 2.2 逻辑函数的化简 2.2.1 代数化简法 2.2.2 卡诺图化简法

第2章布尔代数基础 概述 研究数字系统中逻辑电路设计和分析的数学工具是布尔代数。 布尔代数是由逻辑变量集K(A、B、C、.),常量“0” “1”以及“与”、“或”、“非”3种基本逻辑运算构成的代数 系统。 逻辑变量集K是布尔代数中变量的集合,它可以用任何字母 表示每亼变是的耶值公熊为鲎量“0”或“1” 在数字系统审使用布宗变量表示并关龟路的输入或输出。这 些变量的每一个取值是“0”或“1”两个不相同的值。“0”可 以代表低电压,“1”可以代表高电压。F(False)和T(True)也 可以用于表示“0”或“1” 布尔代数把矛盾的一方假设为“1”,另一方假设为“0”, 使之数学化。 这样可以使用布尔代数中的公理和定理对物理现象作数学演 算,达到逻辑推理的目的
第2章 布尔代数基础 概述 研究数字系统中逻辑电路设计和分析的数学工具是布尔代数。 布尔代数是由逻辑变量集K(A、B、C、.),常量“0”、 “1”以及“与”、“或”、“非”3种基本逻辑运算构成的代数 系统。 逻辑变量集K是布尔代数中变量的集合,它可以用任何字母 表示,每个变量的取值只能为常量“0”或“1”。 在数字系统中使用布尔变量表示开关电路的输入或输出。这 些变量的每一个取值是“0”或“1”两个不相同的值。“0”可 以代表低电压,“1”可以代表高电压。F( False )和T( True )也 可以用于表示“0”或“1”。 布尔代数把矛盾的一方假设为“1”,另一方假设为“0”, 使之数学化。 这样可以使用布尔代数中的公理和定理对物理现象作数学演 算,达到逻辑推理的目的

第2章布尔代数基础 概述 幸运的是,在数字系统中采用的是“0”和“1”两个不 同的值。因此布尔代数可以用来作为分析和设计逻辑电路的数 学工具。 从应用的角度,布尔代数应用于逻辑电路领域称其为逻辑 代数。 本章介绍逻辑代数的基本理论和运算方法,其中包括逻辑 代数基本概念,逻辑函数的定义,逻辑代数的公理、定理和规 则,小项与大项的概念以及使用小项和大项表达逻辑函数的标 准形式。 在此基础上,介绍应用逻辑代数法和卡诺图法化简逻辑函 数的原理与方法
第2章 布尔代数基础 概述 幸运的是,在数字系统中采用的是“0”和“1”两个不 同的值。因此布尔代数可以用来作为分析和设计逻辑电路的数 学工具。 从应用的角度,布尔代数应用于逻辑电路领域称其为逻辑 代数。 本章介绍逻辑代数的基本理论和运算方法,其中包括逻辑 代数基本概念,逻辑函数的定义,逻辑代数的公理、定理和规 则,小项与大项的概念以及使用小项和大项表达逻辑函数的标 准形式。 在此基础上,介绍应用逻辑代数法和卡诺图法化简逻辑函 数的原理与方法

第2章布尔代数基础 2.1逻辑代数基础 2.1.1逻辑代数的基本概念 逻辑代数包含逻辑变量集K(A、B、C、.),每个变量的取 值只可能为常量“0”或“1”。这里的“0”和“1”没有量的 概念,是用来表达矛盾双方,是一种形式上的符号。 逻辑代数中逻辑变量之间是逻辑关系。逻辑关系用逻辑运算 符表示。使用逻辑运算符连接逻辑变量及常量“0”或“1”构成 逻辑代数表达式。 采用逻辑代数表示逻辑电路的输入与输出之间的逻辑关系, 称逻辑函数。这种电路称数字逻辑电路。 逻辑函数除了使用逻辑代数表示以外,还可以使用一种称为 “真值表”的表格表示
第2章 布尔代数基础 2.1 逻辑代数基础 2.1.1 逻辑代数的基本概念 逻辑代数包含逻辑变量集K(A、B、C、.),每个变量的取 值只可能为常量“0”或“1”。这里的“0”和“1”没有量的 概念,是用来表达矛盾双方,是一种形式上的符号。 逻辑代数中逻辑变量之间是逻辑关系。逻辑关系用逻辑运算 符表示。使用逻辑运算符连接逻辑变量及常量“0”或“1”构成 逻辑代数表达式。 采用逻辑代数表示逻辑电路的输入与输出之间的逻辑关系, 称逻辑函数。这种电路称数字逻辑电路。 逻辑函数除了使用逻辑代数表示以外,还可以使用一种称为 “真值表”的表格表示

第2章布尔代数基础 2.1逻辑代数基础 真值表是由输入变量所有可能取值的组合与这些组合值对应 的输出变量的值构成的表格。真值表分为左、右两个部分。 左边部分每一列是输入变量的名字。右边部分的每一列是输 出变量的名字。左边部分是输入变量所有的取值的组合。 如果一个逻辑函数有n个变量,则输入变量所有的取值有2” 个组合。右边部分是把左边每一行输入变量的取值带到逻辑函 数中去运算,把运算的结果“0”或者“1”填进来。这样就完 成了把逻辑函数用真值表表示。 逻辑函数有的比较简单,有的相当复杂。但是它们都是 由“与”、“或”、“非”三种最基本的逻辑运算构成。下面 分别介绍这三种逻辑运算符、逻辑表达式、逻辑函数和逻辑函 数符号
第2章 布尔代数基础 2.1 逻辑代数基础 真值表是由输入变量所有可能取值的组合与这些组合值对应 的输出变量的值构成的表格。真值表分为左、右两个部分。 左边部分每一列是输入变量的名字。右边部分的每一列是输 出变量的名字。左边部分是输入变量所有的取值的组合。 如果一个逻辑函数有n个变量,则输入变量所有的取值有2 n 个组合。右边部分是把左边每一行输入变量的取值带到逻辑函 数中去运算,把运算的结果“0”或者“1”填进来。这样就完 成了把逻辑函数用真值表表示。 逻辑函数有的比较简单,有的相当复杂。但是它们都是 由“与”、“或”、“非”三种最基本的逻辑运算构成。下面 分别介绍这三种逻辑运算符、逻辑表达式、逻辑函数和逻辑函 数符号

第2章布尔代数基础 2.1逻辑代数基础 1.逻辑函数符号 如前所述,逻辑函数是由“与”、“或”、“非”三种最基 本的逻辑运算构成。为了象表示电阻、电容和三极管一样,用图 形化的方式表示不同的逻辑函数,美国国家标准学会(the American National Standards Institute,ANSl)和美国电气与电 子工程师协会(the Institute of Electrical and Electronic Engineers,IEEE)在1984年制定了一个逻辑函数符号标准。如 图2-1所示。 逻辑函数符号的标识 输入变量 输出变量 图2-1EEE通用逻辑函数符号
第2章 布尔代数基础 2.1 逻辑代数基础 1. 逻辑函数符号 如前所述,逻辑函数是由“与”、“或”、“非”三种最基 本的逻辑运算构成。为了象表示电阻、电容和三极管一样,用图 形化的方式表示不同的逻辑函数,美国国家标准学会( the American National Standards Institute, ANSI )和美国电气与电 子工程师协会(the Institute of Electrical and Electronic Engineers, IEEE) 在1984年制定了一个逻辑函数符号标准。如 图2-1所示
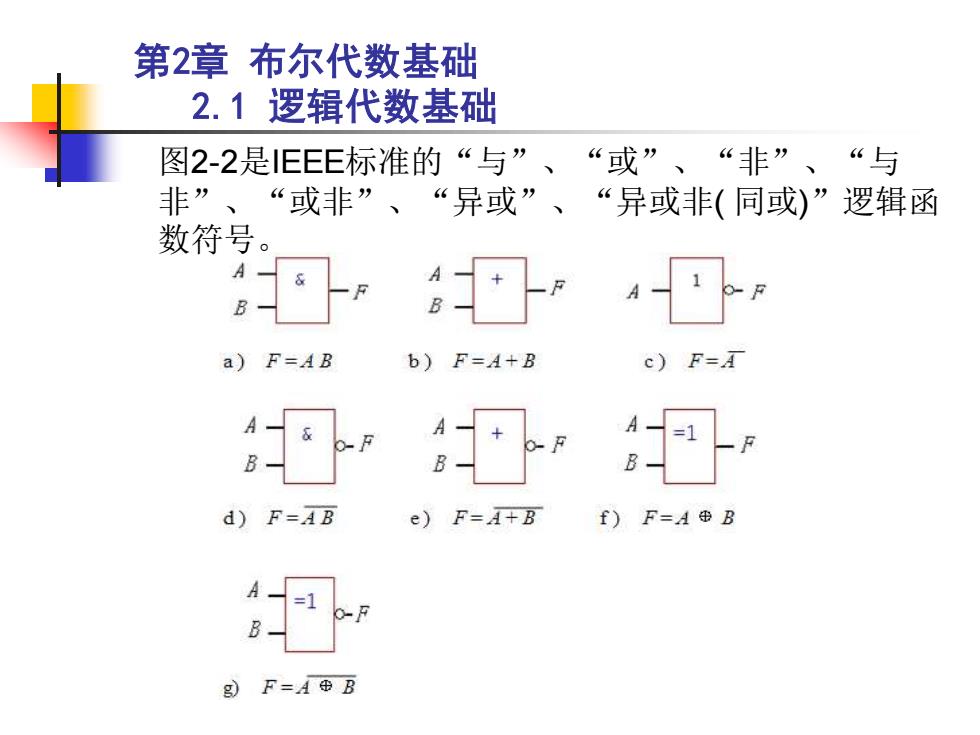
第2章布尔代数基础 2.1逻辑代数基础 图2-2是EEE标准的“与”、“或”、“非”、“与 非”、“或非”、“异或”、“异或非(同或)”逻辑函 数符号: a)F=AB b)F=A+B c)F=A A-8 d)F=AB e)F-A+B f)F=A⊕B g)F=A⊕B
第2章 布尔代数基础 2.1 逻辑代数基础 图2-2是IEEE标准的“与”、“或”、“非”、“与 非”、“或非”、“异或”、“异或非( 同或)”逻辑函 数符号

第2章布尔代数基础 2.1逻辑代数基础 2.“与”运算 “与”运算的运算符是“.”、 “*”、“A”或是空。在本 书中使用“”表示“与”运算符。“与”运算的定义如表2-1所 示。F=AB是“与”运算逻辑函数。“AB”称为F的“与”运 算表婪式或”运算 3. “或”运算的运算符是“+”、“V”。本书中使用“+”表 示“或”运算符。“或”运算的定义如表2-2所示。F=A+B是 “或”运算逻辑函数。“A+B”称为F的“或”运算表达式。 4.“非”运算 “非”运算的运算符是“”或“”,本书中使用“”表 示“非”运算符。“非”运算的定义如表2-3所示。F=A是“非” 运算逻辑函数。A是“非”运算的逻辑表达式。在逻辑函数中,A 称为反变量,A称为原变量
第2章 布尔代数基础 2.1 逻辑代数基础 2.“与”运算 “与”运算的运算符是“·”、“*”、“∧”或是空。在本 书中使用“”表示“与”运算符。“与”运算的定义如表2-1所 示。F = A B是“与”运算逻辑函数。“A B”称为F的“与”运 算表达式。 3.“或”运算 “或”运算的运算符是“+”、“∨”。本书中使用“+”表 示“或”运算符。“或”运算的定义如表2-2所示。F = A + B是 “或”运算逻辑函数。“A + B”称为F的“或”运算表达式。 4.“非”运算 “非”运算的运算符是“ ”或“ ” ,本书中使用“ ” 表 示“非”运算符。“非”运算的定义如表2-3所示。F = A是“非” 运算逻辑函数。A是“非”运算的逻辑表达式。在逻辑函数中,A 称为反变量,A称为原变量

第2章布尔代数基础 2.1逻辑代数基础 5.“异或”运算 “异或”运算的运算符是“⊕”。“异或”运算的定义如表 2-4所示。F=A⊕B是“异或”运算逻辑函数。“异或”运算 逻辑函数还可以用F=AB+AB表示。 6.“同或”运算 “同或”运算的运算符是“⊙”。“同或”运算的定义如 表2-5所示。F=A⊙B是“同或”运算逻辑函数。“同或”运算 逻辑函数还可以用F=AB+AB表示。 “异或”运算表达式与“同或”运算表达式有如下关系: A⊕B=A⊙B,A⊙B=A⊕B
第2章 布尔代数基础 2.1 逻辑代数基础 5.“异或”运算 “异或”运算的运算符是“⊕”。“异或”运算的定义如表 2-4所示。F = A ⊕ B是“异或”运算逻辑函数。 “异或”运算 逻辑函数还可以用F = A B + A B表示。 6.“同或”运算 “同或”运算的运算符是“⊙”。“同或”运算的定义如 表2-5所示。F = A ⊙ B是“同或”运算逻辑函数。“同或”运算 逻辑函数还可以用F = A B + A B表示。 “异或”运算表达式与“同或”运算表达式有如下关系: A ⊕ B = A ⊙ B,A ⊙ B = A ⊕ B

第2章布尔代数基础 2.1逻辑代数基础 2.1.2逻辑函数 上面从逻辑代数的角度介绍了逻辑函数。下面从逻辑电路的角度讨论逻辑函 数。设一个由逻辑函数符号构成的逻辑电路,它的输入变量为41,4,.,A, 输出变量为F,如图2-3所示。当41,.,An的取值确定以后,F的值就唯 一确定下来,则称F是A1,A,.,A的逻辑函数,记为F=f(4.4。.,A)。 逻辑电路 输入变量 A 输出变量 An 图2-3逻辑函数的定义
第2章 布尔代数基础 2.1 逻辑代数基础 2.1.2逻辑函数