
第四章导数的应用问题 4.1中值定理 4.2洛必达法则 4.3函数的单调性与极值
第四章 导数的应用问题 4.1 中值定理 4.2 洛必达法则 4.3 函数的单调性与极值

4.2洛必达法则 两个基本类型不定式解法(洛必达法则) 如果当x→(或x→o)时,两个函数f(x) 与g(x)都趋于零(或都趋于无穷大,那末极限 1imf称为(或°)型不定式. 8(x) 0 00 例如, tanx lim lim →0 x→+olnx 思考:两个无穷小量的比(两个无穷大量的比)的极限是什么? 常数C 不存在?
4.2 洛必达法则 一 . 两个基本类型不定式解法(洛必达法则) ( ) , ( ) ( ) , ( ) 0 lim . ( ) 0 x a x f x g x f x g x → → 如果当 或 时 两个函数 与 都趋于零(或都趋于无穷大)那末极限 称为 (或 )型不定式 例如, , tan lim 0 x x x→ + 2 lim , x ln x → x ) 0 0 ( ( ) 思考:两个无穷小量的比(两个无穷大量的比)的极限是什么? 0 常数C 不存在?

4.2洛必达法则 0 型不定式 0 定理 如果函数f(x)和g(x)满足 (1)当x→或x→o时,函数f(x)→0,8g(x)→0; (2)f'(x)和g'(x)都存在,且g'(x)≠0; 3)lime存在(或为无穷大; 8'(x) 则1imf=limf'() 8(x) g'(x) 若用了一次洛必达之后,仍符合洛必达条件,则可继续使用 洛必达法则!
4.2 洛必达法则 ( ( ) (1) , ( ) 0, ( ) 0; (2) ( ) '( ) '( ) 0; ( ) (3) lim ( ); '( ) ( ) ( ) lim lim . ( ) '( ) f x g x x a x f x g x f x g x g x f x g x f x f x g x g x → → → → = 如果函数 )和 满足 当 或 时 函数 和 都存在,且 存在 或为无穷大 则 定理 若用了一次洛必达之后,仍符合洛必达条件,则可继续使用 洛必达法则! 0 1. 0 型不定式
4.2洛必达法则 f(x)→0,g(x)→0 lim)=lim sinx 8(x) g'(x) 例题1 求lim x→0 解 由于满足洛必达法则的条件 原式=im (s)-lim OSx x→0 (x)' x-→0 1 =1. 例题2 求im- x3-3x+2 x1x3-x2-x+11 检查不满足 解 由于满足洛必达法则的条件 定理条件! 原式=im、 3x2-3 6x 3 lim t→13x2-2x-1x16x-2 2
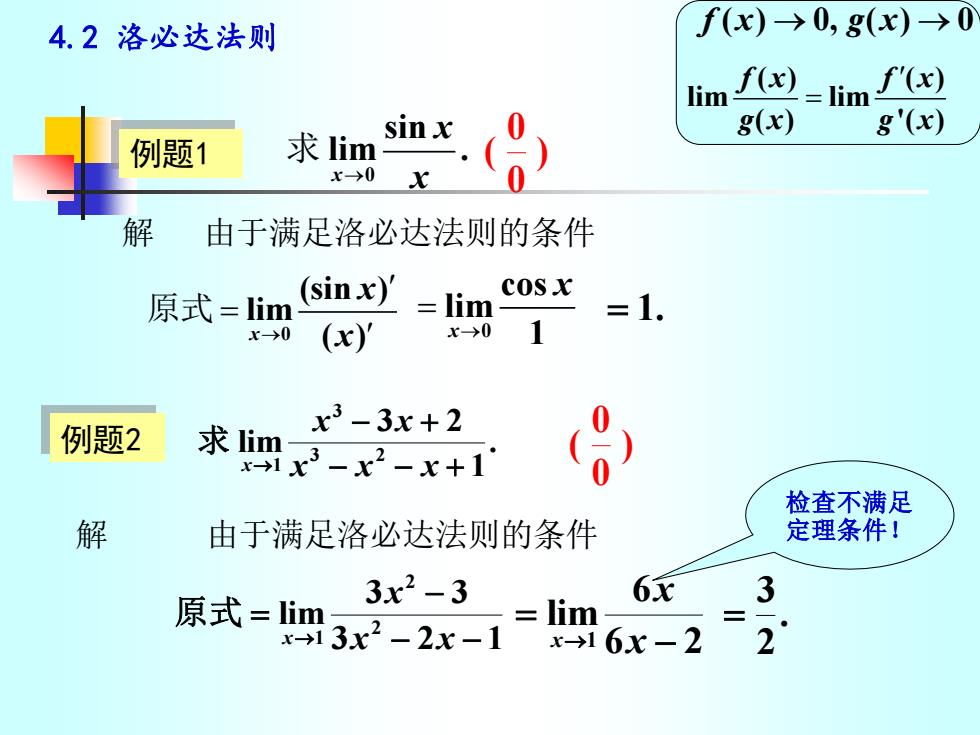
4.2 洛必达法则 例题1 解 由于满足洛必达法则的条件 0 sin lim . x x → x 求 0 (sin ) lim ( ) x x → x = 原式 0 cos lim x 1 x → = = 1. 例题2 . 1 3 2 lim 3 2 3 1 − − + − + → x x x x x x 求 3 2 1 3 3 lim 2 2 1 − − − = → x x x x 原式 6 2 6 lim 1 − = → x x x . 2 3 = ) 0 0 ( ) 0 0 ( 检查不满足 定理条件! f x g x ( ) 0, ( ) 0 → → ( ) ( ) lim lim ( ) '( ) f x f x g x g x = 解 由于满足洛必达法则的条件

4.2洛必达法则 2.”型不定式 00 定理 如果函数f(x)和g(x)满足 (①)当x→a或x→o时,函数f(x)→o,g(x)→o; (2)f'(x)和g'(x)都存在,且g'(x)≠0; (3)1im四存在(或为无穷大片 8'(x) 则imf9=1imf'x) g(x) g'(x) 若用了一次洛必达之后,仍符合洛必达条件,则可继续 使用洛必达法则!
4.2 洛必达法则 ( ( ) (1) , ( ) , ( ) ; (2) ( ) '( ) '( ) 0; ( ) (3) lim ( ); '( ) ( ) ( ) lim lim . ( ) '( ) f x g x x a x f x g x f x g x g x f x g x f x f x g x g x → → → → = 如果函数 )和 满足 当 或 时 函数 和 都存在,且 存在 或为无穷大 则 定理 2. 型不定式 若用了一次洛必达之后,仍符合洛必达条件,则可继续 使用洛必达法则!
4.2洛必达法则 f(x)→o,g(x)-→0 lim f) )-limf(x) Inx 8(x 8'(x) 例题3 求im 解 由于满足洛必达法则的条件 1 原式=im (Inx)' 1 1 lim =二lim +xn→mx =0. 例题4 求lim e ( 还是”型,继续 0 解 由于满足洛必达法则的条件 用洛必达法则 原式=lim ( lim x2"2x lim (e)' t =十00 x+0(2x)' lim x-→+2
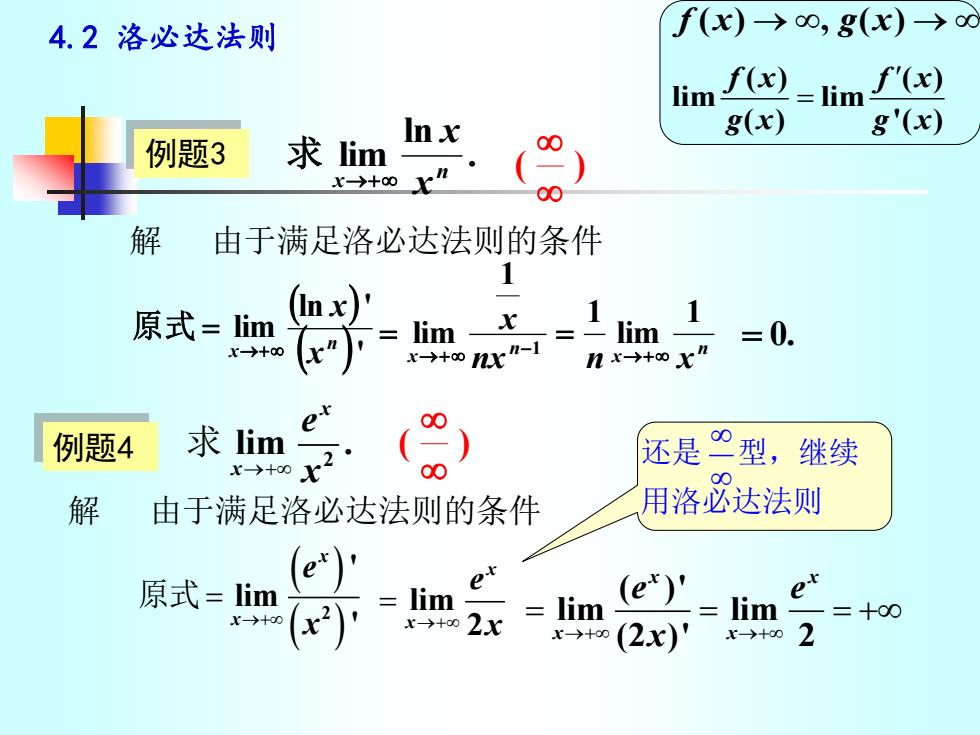
4.2 洛必达法则 例题3 . ln lim n x x x →+ 求 ( ) ( )' ln ' lim n x x x →+ 原式 = n x n x nx n x x 1 lim 1 1 lim 1 →+ − →+ = = = 0. ( ) 解 由于满足洛必达法则的条件 f x g x ( ) , ( ) → → ( ) ( ) lim lim ( ) '( ) f x f x g x g x = 例题4 2 lim . x x e →+ x 求 ( ) ( ) 2 ' lim ' x x e x →+ 原式 = lim 2 x x e →+ x = ( ) 解 由于满足洛必达法则的条件 ( )' lim lim (2 )' 2 x x x x e e →+ →+ x = = = + 还是 型,继续 用洛必达法则
4.2洛必达法则 二. 0∞,0-0,0°,1”,0型未定式解法 关键:将其它类型未定式化为洛必达法则可解决的类型 1.0o0型 步骤: 0.00→ ·00, 或00→0. 0 0 例题5 求5mt(了-arctanx). (0.∞) X>+00 π 1 一 arctanx 解原式=im lim 1+x2= 1 lim =lim X>+00 x-→+0 1 +∞1+x2 2二1 x-+02X x 型 00 型 0 0
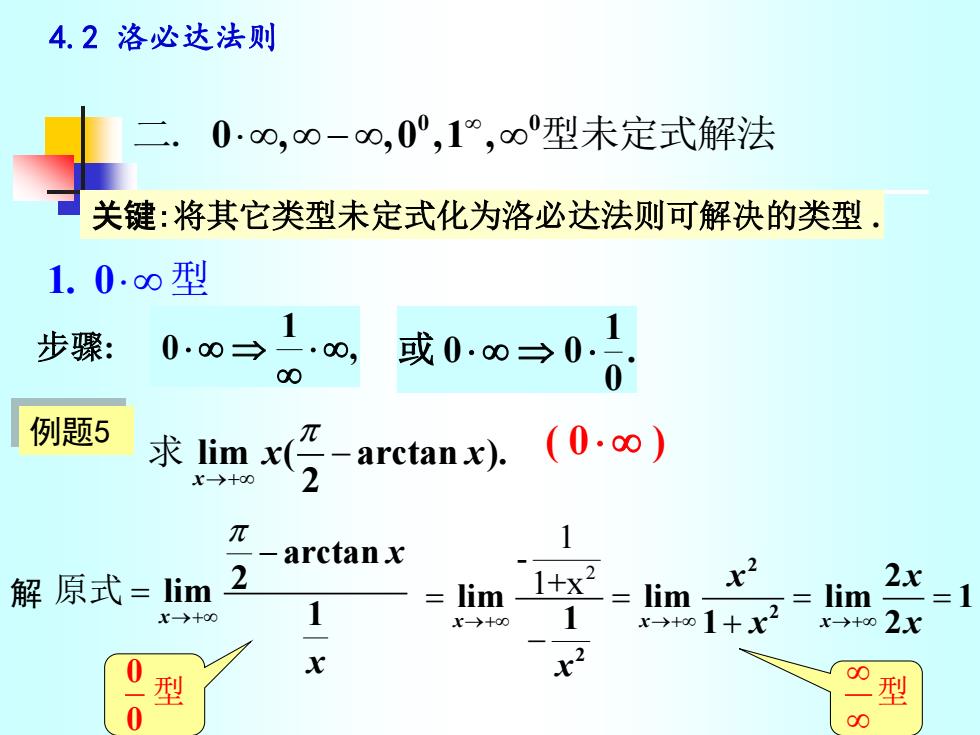
4.2 洛必达法则 0 0 0 , ,0 ,1 , 二. − 型未定式解法 例题5 解 lim ( arctan ). x 2 x x →+ 求 − ( 0 ) arctan 2 limx 1 x x →+ − 原式 = 关键:将其它类型未定式化为洛必达法则可解决的类型 . 0 0 型 型 1. 0 型 步骤: , 1 0 . 0 1 或 0 0 2 1 - 1+x 2 2 2 2 lim lim lim 1 x x x 1 1 2 x x x x x →+ →+ →+ = = = = + −
4.2洛必达法则 2.00-00型 11 0-0 步骤: 00-00→ 00 0.0 例题6 求im( 1 ).(0-00) x-→0`sinxx 解 原式=lim x-sinx lim x-sinx x-→0x·sinx x→0 1-cosx sinx lim =lim 0 =0. 型 x-→0 2x x→0 2 0
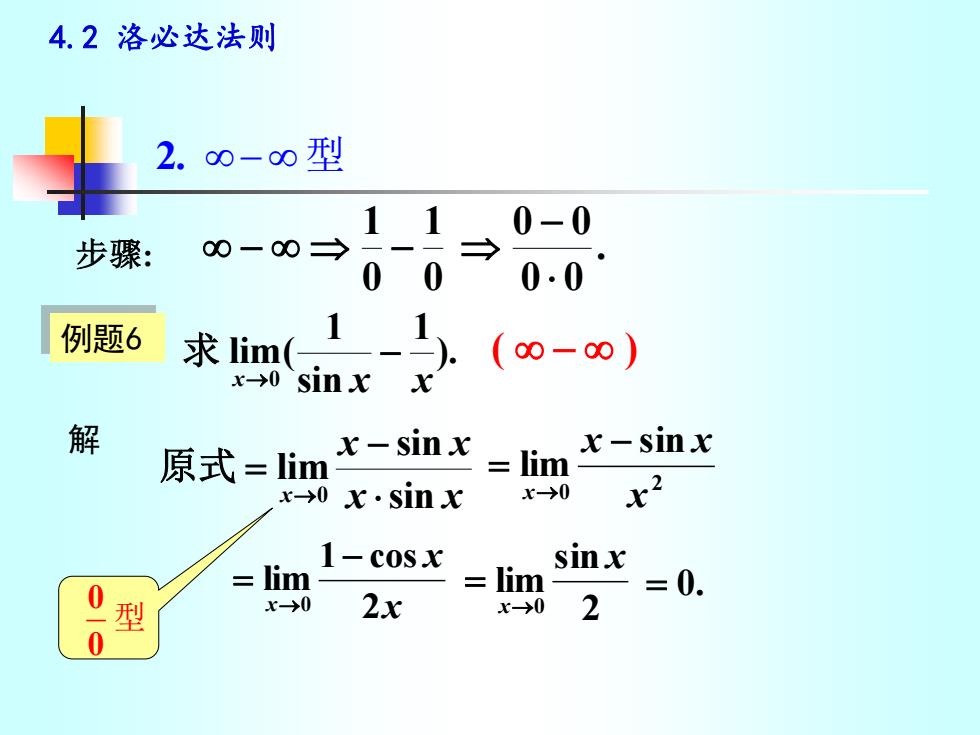
4.2 洛必达法则 例题6 解 ). 1 sin 1 lim( x 0 x x − → 求 ( − ) 0 1 0 1 − − . 0 0 0 0 − x x x x x sin sin lim 0 − = → 原式 x x x 2 1 cos lim 0 − = → = 0. 2. − 型 步骤: 2 0 sin lim x x x x − = → 2 sin lim 0 x x→ = 0 0 型

4.2洛必达法则 2.其它类型 注意:洛必达法则的使用条件 洛必达法则只能对9或”型未定式使用, 0 0°型 步骤: 取对数nr0n50成女到 1”型 步骤: 取对数1n1→0.0三0.1(或0) 类似的方法可以得到∞型的步骤,试一试?
4.2 洛必达法则 注意:洛必达法则的使用条件. 0 . 0 洛必达法则只能对 或 型未定式使用 2. 其它类型 0 1 1 ln 0 0 0 ( ) 0 取对数 或 0 0 型 步骤: 1 1 ln1 0 ( 0) 0 取对数 或 1 型 步骤: 类似的方法可以得到 0 型的步骤,试一试?

思考与练习 1.洛必达法则适用于那些情形的极限问 题? 2.求下列极限:
思考与练习 1.洛必达法则适用于那些情形的极限问 题? 2.求下列极限: