
第四节极限的运算 米 ✉囧
第四节 极限的运算

定理 设m/八四=A8(=B, 则(0)Iim[f,±g(x]=limf(x)±lim8() x→X0 =A士B, ②)fW8=mf-s)=AB, 3)血Cf(x)=C.limf(x)=CA(C为常数 X→X0 ✉合
0 0 lim ( ) , lim ( ) , x x x x f x A g x B → → 设 = = 0 0 0 (1) lim ( ) ( ) lim ( ) lim ( ) ; x x x x x x f x g x f x g x A B → → → = = 0 0 0 (2) lim ( ) ( ) lim ( ) lim ( ) ; x x x x x x f x g x f x g x A B → → → = = 则 定理 0 0 lim ( ) lim ( ) ( x x x x Cf x C f x CA C → → (3) = = 为常数)

m[fr-[m)=f(w为正整数) f(x) lim f(x) (3)lim x->xo A (B≠0) x→g(x)limg(x) B ✉囧
0 0 lim ( ) lim ( ) ( n n n x x x x f x f x A n → → = = 为正整数) 0 0 0 lim ( ) ( ) (3) lim ( 0) ( ) lim ( ) x x x x x x f x f x A B g x g x B → → → = =

例11im(3x2-2x+6) x→2 解:lim(3x2-2x+6)=3limx]-2limx+lim6 x→2 x→2 =3×22-2×2+6=14 米 ✉合
2 2 1 lim(3 2 6) x x x → 例 − + 2 2 2 2 2 2 lim(3 2 6) 3[lim ] 2lim lim6 x x x x x x x x → → → → 解: − + = − + 2 = − + = 3 2 2 2 6 14

例2求lim x3-1 x-3x+5 lim(x2-3x+5)limx2-lim3x+lim5 x->2 x→2 x→2 x→2 =(lim x)2-3lim x+lim5 x->2 x→2 x→2 =22-3.2+5=3≠0, x3-1 lim x3-lim 1 ∴.lim x→2 x→2 x2x2-3x+5 lim(x2-3x+5) 23-1 7 3 3
例 2 . 3 5 1 lim 2 3 2 − + − → x x x x 求 解 lim( 3 5) 2 2 − + → x x x lim lim 3 lim 5 2 2 2 → 2 → → = − + x x x x x (lim ) 3lim lim5 2 2 2 →2 → → = − + x x x x x 2 3 2 5 2 = − + = 3 0 , 3 5 1 lim 2 3 2 − + − → x x x x lim ( 3 5 ) lim lim 1 2 2 2 3 2 − + − = → → → x x x x x x . 37 = 3 2 1 3 − =

x2-1 例3求im x1x2+2x-3 解x→1时,分子,分母的极限都是零 先约去极限为零的因子x-1后再求极限 x2-1 (x+1)(x-1) lim- =lim x1x2+2x-31(x+3)(x-1) x+11 lim x→1X+3 2 (消去零因子法) 作米 >合
解 例3 . 2 3 1 lim 2 2 1 + − − → x x x x 求 x →1时,分子,分母的极限都是零. 先约去极限为零的因子x −1后再求极限. ( 3)( 1) ( 1)( 1) lim 2 3 1 lim 1 2 2 1 + − + − = + − − → → x x x x x x x x x 3 1 lim 1 + + = → x x x . 2 1 = (消去零因子法)
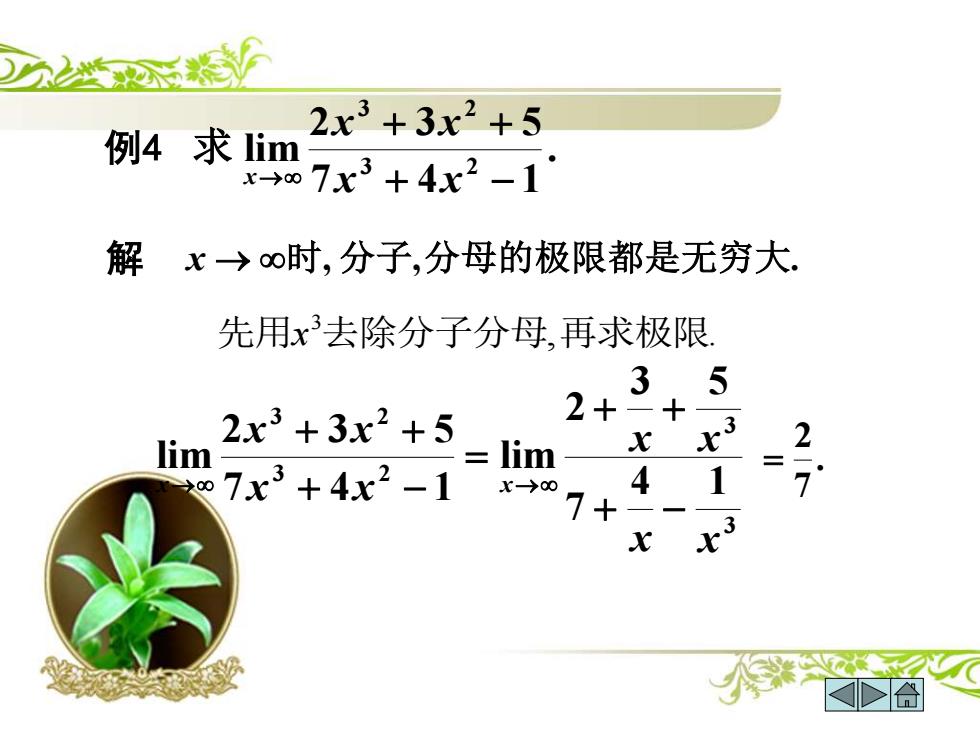
2x3+3x2+5 例4求lim X-→0 7x3+4x2-1 解x→o时,分子,分母的极限都是无穷大. 先用x3去除分子分母,再求极限 3.5 2x3+3x2+5 2+ 一十 lim =lim 2 007x3+4x2-1K-→0 4 1 · ✉囧
例 4 . 7 4 1 2 3 5 lim 3 2 3 2 + − + + → x x x x x 求 解 x → 时, 分子,分母的极限都是无穷大. , . 先用x3 去除分子分母 再求极限 33 3 2 3 2 4 1 7 3 5 2 lim 7 4 1 2 3 5 lim x x x x x x x x x x + − + + = + − + + → → . 72 =

3x2-2x-1 例5lim X→00 2x3-x2+5 321 解:lim 3x2-2x-1 =lim k02x3-x2+5 x-0 2-1+5 一十 3lim2lim 1 -lim3 x→0Xx→0X2x→0X3 0 0 1 1 lim 2-lim+5lim 2 X→00 x-→0Xx-→o0X1 米 合
2 3 2 3 2 1 5lim . x 2 5 x x → x x − − − + 例 2 3 2 3 2 1 x 2 5 x x lim → x x − − − + 解: 2 3 3 3 2 1 lim 1 5 2 x x x x x x → − − = − + 2 3 3 1 1 1 3lim 2lim lim 1 1 lim 2 lim 5lim x x x x x x x x x x x → → → → → → − − = − + 0 0 2 = =

例6求im( ,2 2 n-→on 解 先变形再求极限。 lim( ,2 n 2)=lim 1+2+.+n n-→o几 1→co n(n+1) lim 2 1 1n-→oo n2 n-→∞2 米 ✉囧
例6 ). 1 2 lim( 2 2 2 n n n n n + + + → 求 解 2 2 2 2 1 2 ) lim 1 2 lim( n n n n n n n n + + + + + + = → → 2 ( 1) 2 1 lim n n n n + = → ) 1 (1 2 1 lim n n = + → . 2 1 = 先变形再求极限

2”-1 例71im n>∞ 4n+1 2”-1 解:lim 2”-1 =lim 2”-1 lim 22m n∞4”+1 n∞22m+1 n→00 22m+1 11 23 1 =lim 2” 22m lim (lim n-02n n→)n n->oo 1+ 23 1+(im 、2 0. 米 ✉合
2 1 7 lim . 4 1 n n n→ − + 例 2 2 1 2 1 lim lim 4 1 2 1 n n n n n n → → − − = + + 解: 0. 1 0 = = 2 2 2 2 1 2 lim 2 1 2 n n n n n → − = + 2 2 1 1 2 2 lim 1 1 2 n n n n → − = + 2 2 1 1 lim (lim ) 2 2 1 1 (lim ) 2 n n n n n n → → → − = +