
第六节两个重要极限 米吃 ✉合
第六节 两个重要极限
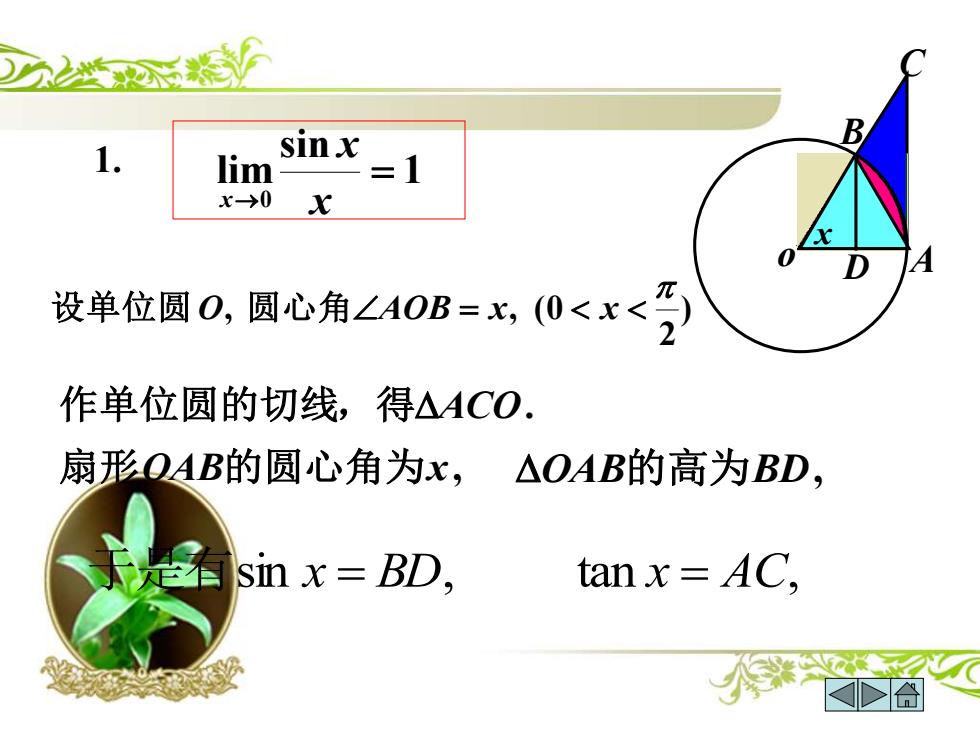
D 1. sinx lim =1 x→0 X 设单位圆0,圆心角∠40B=x0<r<受 作单位圆的切线,得△ACO. 扇形OAB的圆心角为x,△OAB的高为BD, f是有sinx=BD, tanx=AC
A C 1. 1 sin lim 0 = → x x x ) 2 , , (0 设单位圆 O 圆心角AOB = x x 于是有sin x = BD, tan x = AC, x o B D 作单位圆的切线,得ACO. 扇形OAB的圆心角为x, OAB的高为BD

.'sinx0 x→0 x
sin x x tan x, 1, sin cos x x 即 x 0 . 2 上式对于 也成立 − x , 2 当 0 时 x 0 cos x − 1 = 1 − cos x 2 2sin2 x = 2 ) 2 2( x , 2 2 x = 0, 2 lim 2 0 = → x x lim(1 cos ) 0, 0 − = → x x limcos 1, 0 = → x x lim1 1, 0 = x→ 又 1. sin lim 0 = → x x x

第一个重要极限: sinx lim =1 x→0 sln△ lim =1 △-→>0 △ 例如:lim sin9x =1 9x0 9x 作米 ✉囧
1 sin lim 0 = → x x x 1 si lim 0 = → n 1 9 si 9 lim 9 0 = → x n x x 例如: 第一个重要极限:

例1 求lim sin 2x x>0 x 解:lim sin 2x sin 2x lim .2 sin 2x =2lim x-→0 x→0 2x x→0 2x sin 2x =21im 2×1=2 2x→02x 米 ✉合
0 sin 2 1 lim . x x → x 例 求 0 sin 2 lim x x → x 解: 0 sin 2 lim( 2) x 2 x → x = 0 sin 2 2lim x 2 x → x = 2 1 2 2 sin 2 2 lim 2 0 = = = → x x x

tan x 例2求lim x→0 X 解: tanx lim sin x 1 x→0 lim = x->0 cos x tanx sinx 1 lim lim lim x→0X X→0 X x→0C0SX =1×1 =1. ✉囧
0 tan 2 lim . x x → x 例 求 0 tan lim x x → x 解: = 1 10 sin 1 lim cos x x → x x = =1

1- 例3求im COSx x→0 x2 2sin2 2sin2 解原式=lim 2 lim 2 x->0 t? x-→0 4. sin =m 2)2 1 2 2x0 2 2 米 ✉合
例 3 . 1 cos lim 2 0 x x x − → 求 解 22 0 2 2sin lim x x x → 原式 = 2 2 0 ) 2 4 ( 2 2 sin lim x x x = → 2 0 2 ) 2 2 sin lim ( 21 x x x → = 2 1 21 = . 21 =

cos a 例4求1im ar 2 解: 因为cosa=sin2 所以lim cosa=lim sin( -) π π → 2 - a→ -a 2 7 si lim 2-a-0 π 2
2 cos 4 lim . 2 → − 例 求 cos sin( ), 2 解:因为 = − 2 2 sin( ) cos 2 lim lim . 2 2 → → − = − − 所以 1 2 ) 2 sin( lim 0 2 = − − = − →

2. lim(1+)*=e 先列表考察当x→+0及x→-0时,函数(1+)的变化趋势 X 1 2 5和 10e 100P 1000P 10000P 100000- .+十003 1+白) 2 225 2.49 259 2.705 2.717 2.718 2.718274 x和 -103 -100 -1000 -10000 -100000e .+-002 1+) 2.88 2.732 2.720 2.7183 2.71828 从上表可以看出, 当x→+0或x→-0时,函数((1+白)产的对应值无限地趋近于 X 一个确定的数2.71828
2. e x x x + = → ) 1 lim(1

么心米 第二个 重要极限 lim1+)'=e台lim(1+x)元=e X-→0 设z=二,则当x→∞时,2→0 X 则lim(1+z)F=e. 2→0 0-e (+A)s -e 米 ✉囧
1 lim(1 )x x e → x 重要极限 + = 1 z x z , 0 x 设 = → → 则当 时, 1 0 lim(1 ) . z z z e → 则 + = + = e → 1 0 lim (1 ) 第二个 = e + → ) 1 lim (1 1