
第一章函数、极限与连续 1.1函数的概念 1.1.1基本初等函数 我们把幂函数y=x“(a为实数),指数函数y=a(a>0且a≠1),对数函数 y=log。x(a>0且a≠1),三角函数和反三角函数统称为基本初等函数. 注:作为基本初等函数的三角函数仅有六个函数:y=smx:y=cosx:y=tanx: y=cotx:y=secx:y=cscx. 反三角函数仅有四个函数:y=arcsin x:y=arccosx;y=arctanx:y=arccotx. 幂、指、对三大函数的变量只能是x,常数a和a可以取一切实数:随者常数a和a取 不同的值,对应的幂、指、对三大函数有无穷多个基本初等函数。 由基本初等函数与常数经过有限次的四则运算所得到的函数称为简单函数。 例如y=3-2-1和y=】snx+c0sx等都是简单函数. 1.1.2复合函数 如果y是u的函数y=f(w),而u是x的函数u=p(x),我们称y是x的复合函数, 记作y=f(p(x),其中u称为中间变量. 注:函数u=p(x)的值域应在函数y=f(0)的定义域内:若有多个函数复合而成,则中间 变量可用变量,w,1等表示。 例如y=4'和y=arctanx是基本初等函数,y=22和y=arctan2x是复合函数:而 y=arcsin(x2+2)便失去意义 例1指出函数y=5sm32(x2+2)2-3cosx的复合过程. 解由y=5u3-3cosx,u=smv,v=2w2,w=x2+2. 1.1.3初等函数 由基本初等函数和常数经过有限次的四则运算或经过有限次的复合步骤所构成的,并只 用一个解析式子表示的函数叫做初等函数
1 第一章 函数、极限与连续 1.1 函数的概念 1.1.1 基本初等函数 我们把幂函数 y = x ( 为实数),指数函数 x y = a (a 0 且 a 1) ,对数函数 y x a = log (a 0 且 a 1) ,三角函数和反三角函数统称为基本初等函数. 注:作为基本初等函数的三角函数仅有六个函数: y = sin x ; y = cos x ; y = tan x ; y = cot x ; y = sec x ; y = csc x . 反三角函数仅有四个函数: y = arcsin x ; y = arccos x ; y = arctan x ; y = arc cot x . 幂、指、对三大函数的变量只能是 x ,常数 和 a 可以取一切实数;随着常数 和 a 取 不同的值,对应的幂、指、对三大函数有无穷多个基本初等函数. 由基本初等函数与常数经过有限次的四则运算所得到的函数称为简单函数. 例如 = 3 2 −1 x y 和 y sin x cos x 2 1 = + 等都是简单函数. 1.1.2 复合函数 如果 y 是 u 的函数 y = f (u) ,而 u 是 x 的函数 u = (x) ,我们称 y 是 x 的复合函数, 记作 y = f ((x)) ,其中 u 称为中间变量. 注:函数 u = (x) 的值域应在函数 y = f (u) 的定义域内;若有多个函数复合而成,则中间 变量可用变量 u , v, w, s ,t 等表示. 例如 x y = 4 和 y = arctan x 是基本初等函数, x y 2 = 2 和 y = arctan 2x 是复合函数;而 arcsin( 2) 2 y = x + 便失去意义. 例 1 指出函数 y 5sin 2(x 2) 3cos x 3 2 2 = + − 的复合过程. 解 由 y 5u 3cos x 3 = − ,u = sin v, 2 v = 2w , 2 2 w = x + . 1.1.3 初等函数 由基本初等函数和常数经过有限次的四则运算或经过有限次的复合步骤所构成的,并只 用一个解析式子表示的函数叫做初等函数

y=2,y=3sinx,y=2+x,y=sn'2x,y=Inx-1),y=arctan3x 等都是初等函数. 1.2.4分段函数 有些函数虽然也可以用解析式表示,但不能用一个解析式表示,在定义域的不同范围具 有不同的解析式,这样的函数称为分段函数. 「1x>0 y-日0gs4限 -1x0 3.设fx)={0x=0,求f(-),f0),f0,fa) 1-xx<0 4.设fx)=x2-x,求f(白),fx-I),fx+△x)-fx) 1.2函数极限 1.2.1当x→o时的极限 当x→含→-∞) 时的极限: 台x→+0 如图上1所示,考察商数y士的图形。容 易发现不论x→-0或x→+0都有y→0. 我们称该函数当x→o时的极限为0(或f(x) 收敏于O,起作血0该典y0 图1.1 2
2 例如 2 2 x y = ,y = 3sin x ,y = 2 + x ,y sin 2x 3 = ,y = ln( x −1) ,y = arctan 3x 等都是初等函数. 1.2.4 分段函数 有些函数虽然也可以用解析式表示,但不能用一个解析式表示,在定义域的不同范围具 有不同的解析式,这样的函数称为分段函数. 例如 − = = 1 0 0 0 1 0 x x x y , 1 0 2 0 3 x x x y x + = 等都是分段函数. 练习题 1.1 1.指出下列各函数的复合过程: (1) y = x + 3x −1 ; (2) x y e 3 cos 2 − = ; (3) 3ln (2 1) 3 y = x − ; (4) 2 y x = − − arctan sin(2 1) . 2.已知 y = 1+ ln u , 2 1 3 u = v − ,v = sin x ,试把 y 表示成 x 的函数. 3.设 1 0 ( ) 0 0 1 0 x x f x x x x + = = − ,求 f (−1), f (0), f (1) , f x ( ) . 4.设 2 f x x x ( ) = − ,求 1 f ( ) x , f x( 1) − , f x x f x ( ) ( ) + − . 1.2 函数极限 1.2.1 当 x → 时的极限 当 x x x → − → → + 含 时的极限: 如图 1.1 所示,考察函数 x y 1 = 的图形,容 易发现不论 x → −或 x → + 都有 y → 0 . 我们称该函数当 x → 时的极限为 0(或 f x( ) 收敛于 0),记作 x x 1 lim → =0 或 y x→ lim =0. 图 1.1

一般地,当无限地增大时,函数∫(x)无限地趋近于一个固定的常数A,则称当 xo时,∫x)的极限为A(或收敛于A),记为mf(x)=A. 若-x无限地增大时,函数f(x)无限地趋近于一个固定的常数A,则称当x→-0时, fx)的极限为A,记为mf(x)=A. 若x无限地增大时,函数(x)无限地趋近于一个固定的常数A,则称当x→+0时 f(x)的极限为A,记为mf(x)=A. 判断函数f(x)当x→0是否有极限,通常用如下的结论: mf(x)=A的充要条件是mf(x)=mf(x)=A. 例1中0,其中c为常数 例2mg=0,其中4)时f(x)的右极限为A,记为mf)=A
3 一般地,当 x 无限地增大时,函数 f (x) 无限地趋近于一个固定的常数 A ,则称当 x → 时, f (x) 的极限为 A (或收敛于 A ),记为 f x A x = → lim ( ) . 若 − x 无限地增大时,函数 f (x) 无限地趋近于一个固定的常数 A ,则称当 x →− 时, f (x) 的极限为 A ,记为 f x A x = →− lim ( ) . 若 x 无限地增大时,函数 f (x) 无限地趋近于一个固定的常数 A ,则称当 x → + 时 f (x) 的极限为 A ,记为 f x A x = →+ lim ( ) . 判断函数 f (x) 当 x → 是否有极限,通常用如下的结论: f x A x = → lim ( ) 的充要条件是 f x f x A x x = = →− →+ lim ( ) lim ( ) . 例 1 lim = 0 → x c x ,其中 c 为常数. 例 2 lim = 0 →+ x x q ,其中 q 1. 例 3 由于 2 lim arctan = − →− x x 和 2 lim arctan = →+ x x ,所以 x x lim arctan → 不存在(或发散). 例 4 由于 lim 3 = 0 →− x x 和 = + →+ x x lim 3 ,所以 x x lim 3 → 不存在(或发散). 例 5 n n lim (1+ (−1)) →+ 不存在. 例 6 0 (1 ( 1)) lim = + − →+ n n n . 1.2.2 当 0 x → x 时的极限 一般地,当 x 无限地趋近于 0 x 时,函数 f (x) 无限地趋近于一个固定的常数 A ,则称 当 0 x → x 时, f (x) 的极限为 A (或收敛于 A ),记为 f x A x x = → lim ( ) 0 . 若 x 是从左侧无限地趋近于 0 x 时,函数 f (x) 无限地趋近于一个固定的常数 A ,则称当 − → 0 x x ( 0 x x )时, f (x) 的左极限为 A ,记为 f x A x x = → − lim ( ) 0 . 若 x 是从右侧无限地趋近于 0 x 时,函数 f (x) 无限地趋近于一个固定的常数 A ,则称当 + → 0 x x ( 0 x x )时 f (x) 的右极限为 A ,记为 f x A x x = → + lim ( ) 0

判断函数f(x)在点x。处是否有极限,通常用如下的结论: mf9=A的充要条件是1mfx)=1mf)=A. -1=2 例7观察说明x- 挂辐数在-1度处无意义。面首x时,面改一的值的实化8的 x-1 启男是2即号-灯-4=2 x-1 这说明当x→x,时,函数f(x)的极限与在x=x点有没有定义无关:反之,有定义 也未必有极限 x+1x1 限的存在性,若存在则求之 解在x=0,由于mfx)=m(x+)=1,mfx)=lm(x2-)=-1, 所以mf(x)不存在: 在x=1,由于mf(x)=m(x2-)=0,mfx)=m1-x)=0,所以 fx)=0:而mfx)=m1-)=-0.1. 2 例9设f(x)={x 1 x=0求mf. x≠0 巴==0 例10求e
4 判断函数 f (x) 在点 0 x 处是否有极限,通常用如下的结论: f x A x x = → lim ( ) 0 的充要条件是 0 lim ( ) x x f x → − 0 lim ( ) x x f x A → + = = . 例 7 观察说明 2 1 1 lim 2 1 = − − → x x x . 注意到函数 1 1 2 − − x x 在 x =1 点处无意义,而当 x →1 时, 函数 1 1 2 − − x x 的值的变化总的 趋势却是 2. 即 2 1 1 lim x 1 x → x − − 1 ( 1)( 1) lim x 1 x x → x − + = − 1 lim( 1) 2 x x → = + = . 这说明当 0 x → x 时,函数 f (x) 的极限与在 0 x = x 点有没有定义无关;反之,有定义 也未必有极限. 如 0 0 1 1 ( ) − + = x x x x f x ,在 x = 0 有定义,但由于 lim ( ) 1 0 = → − f x x ,lim ( ) 1 0 = − → + f x x ; 即左右极限不相等,所以在 x = 0 点, f (x) 的极限不存在. 例 8 函数 1 0 1 0 1 1 1 ( ) 2 − − − + = x x x x x x f x ,判别函数在 x = 0, x =1, x =1.1 点极 限的存在性,若存在则求之. 解 在 x = 0 ,由于 lim ( ) lim ( 1) 1 0 0 = + = → − → − f x x x x , lim ( ) lim ( 1) 1 2 0 0 = − = − → + → + f x x x x , 所以 lim ( ) 0 f x x→ 不存在; 在 x =1 , 由 于 lim ( ) lim ( 1) 0 2 1 1 = − = → − → − f x x x x , lim ( ) lim (1 ) 0 1 1 = − = → + → + f x x x x ,所以 lim ( ) 0 1 = → f x x ;而 = → lim ( ) 1.1 f x x lim (1 ) 0.1 1.1 − = − → x x . 例 9 设 2 0 ( ) 0 1 x x f x x x = = ,求 lim ( ) 0 f x x→ . 解 lim ( ) 0 f x x→ lim 0 2 0 = = → x x x . 例10 求 x x e 1 0 lim → .

解由于mf)=me产=0,mf)=me=切,所以mf)不存在. 注:(①)对于分段函数求分段点的极限时,若需要用不同的函数,则要用左右极限求解: (2)若在点x。求极限所得到的结果不唯一,则要用左右极限求解. (3)可以用符号0表示极限的结果,但极限不存在不一定是0. 4)m=0.(c为常数). 练习题1.2 上瑞不 1 x-1 x0 极限是否存在 x2+2x-1x≤1 3.设f(x)= 1<x<2,求mf),mfx),盟f),m/). 2x-2 x22 4因-:8表妈四 1.3极限的四则运算 1.3.1极限的四则运算法则 若mf(x)=A与mg(x)=B都存在(其中x→?表示同时有x→x或x→∞), 则有 ①m(f(x)±gx》=limf(x)±gx)=A±B. 注:此公式仅适用于有限项,否则不成立. 知m子++骨+-子+.+丹 ②imfx)g(x)=limf(x)limg(x)=A·B
5 解 由于 lim ( ) lim 0 1 0 0 = = → − → − x x x f x e , = = + → + → + x x x f x e 1 0 0 lim ( ) lim ,所以 lim ( ) 0 f x x→ 不存在. 注:(1)对于分段函数求分段点的极限时,若需要用不同的函数,则要用左右极限求解; (2)若在点 0 x 求极限所得到的结果不唯一,则要用左右极限求解. (3)可以用符号 表示极限的结果,但极限不存在不一定是 . (4) 0 lim 0 x c → x = ,( c 为常数). 练习题 1.2 1.证明: 1 1 lim 1 + + →− x x x 不存在. 2.设 1 0 1 ( ) 1 0 0 x x f x x x x − − = = ,求 f (x) 当 x →0 时的左、右极限,并说明 f (x) 在 x = 0 点 极限是否存在. 3.设 2 2 1 ( ) 2 2 x x f x x x + − = − 2 1 2 1 x x x ,求 lim ( ) 0 f x x→ ,lim ( ) 1 f x x→ ,lim ( ) 2 f x x→ , 3 lim ( ) x f x → . 4. 设 1 0 ( ) 1 0 x x f x x x − = + ,求 lim ( ) 0 f x x→ . 1.3 极限的四则运算 1.3.1 极限的四则运算法则 若 f x A x = → lim ( ) ? 与 g x B x = → lim ( ) ? 都存在(其中 x →? 表示同时有 0 x → x 或 x → ), 则有 ① lim ( ( ) ( )) ? f x g x x → = → lim ( ) ? f x x lim ( ) ? g x x→ = A B . 注:此公式仅适用于有限项,否则不成立. 如 1 2 lim( ) n n → n n n + + + 1 2 lim lim lim n n n n → → → n n n + + + . ② lim ( ) ( ) ? f x g x x→ ? lim ( ) x f x → = lim ( ) ? g x x→ = A B

特殊地有mf(x)=clmf(x)=cA(c为常数)· 品台 (B≠0) 注:应注重法则的前提条件,若前提条件不满足,则法则失效 正确解法:织x如=0, 又如:mW+左-)≠m+左-m反 :产 limcosx ,是错误的写法,因为B=1mx=0. 1.3.2极限的计算方法 1、直接代入法:即mfx)=fx,) 州1 欧 以下各例都无法直接应用法则,需适当的化简后再应用(应清楚每一步求法的根据), 2、(分型:求解的方法是分子和分母同时约去使分母为0的式子.常用的方法有: 因式分解法提取公因式法分子成分母有理化法一。1(下节介留。 r2+r 例2m2x2+x- 格赋-22-号 x(x+1) 3x2+2x 例3期2x+-x 期限式=里新2-2 6
6 特殊地有 lim ( ) ? cf x x→ = c lim ( ) ? f x x→ = cA (c 为常数). ③ ( ) ( ) lim ? g x f x x→ = lim ( ) lim ( ) ? ? g x f x x x → → B A = ( B 0 ). 注: 应注重法则的前提条件,若前提条件不满足,则法则失效. 如: 错误解法: 0 1 lim sin x x → x 0 0 1 lim limsin 0 x x x → → x = = ; 正确解法: 0 1 lim sin 0 = → x x x . 又如: lim ( ) n x x x →+ + − lim lim n n x x x →+ → + − . 再如: 0 0 0 limcos cos lim lim x x x x x x x → → → = ,是错误的写法,因为 0 lim 0 x B x → = = . 1.3.2 极限的计算方法 1、直接代入法:即 lim ( ) ( ) 0 0 f x f x x x = → . 例 1 4 2 3 1 lim 2 2 1 + − − + →− x x x x x . 解 原式 1 ( 1) 4( 1) 2 ( 1) 3( 1) 1 2 2 = − − + − − − − − + = . 以下各例都无法直接应用法则,需适当的化简后再应用(应清楚每一步求法的根据). 2、 ) 0 0 ( 型:求解的方法是分子和分母同时约去使分母为 0 的式子. 常用的方法有: 因式分解法;提取公因式法;分子或分母有理化法; 1 sin lim 0 = → x x x (下节介绍). 例 2 2 1 lim 2 2 1 + − + →− x x x x x . 解 原式 = − + + = →− (2 1)( 1) ( 1) lim 1 x x x x x 3 1 2 1 lim 1 = →− x − x x . 例 3 x x x x x x + − + → 3 2 2 0 2 3 2 lim . 解 原式 2 2 1 3 2 lim 2 0 = − + − + = → x x x x
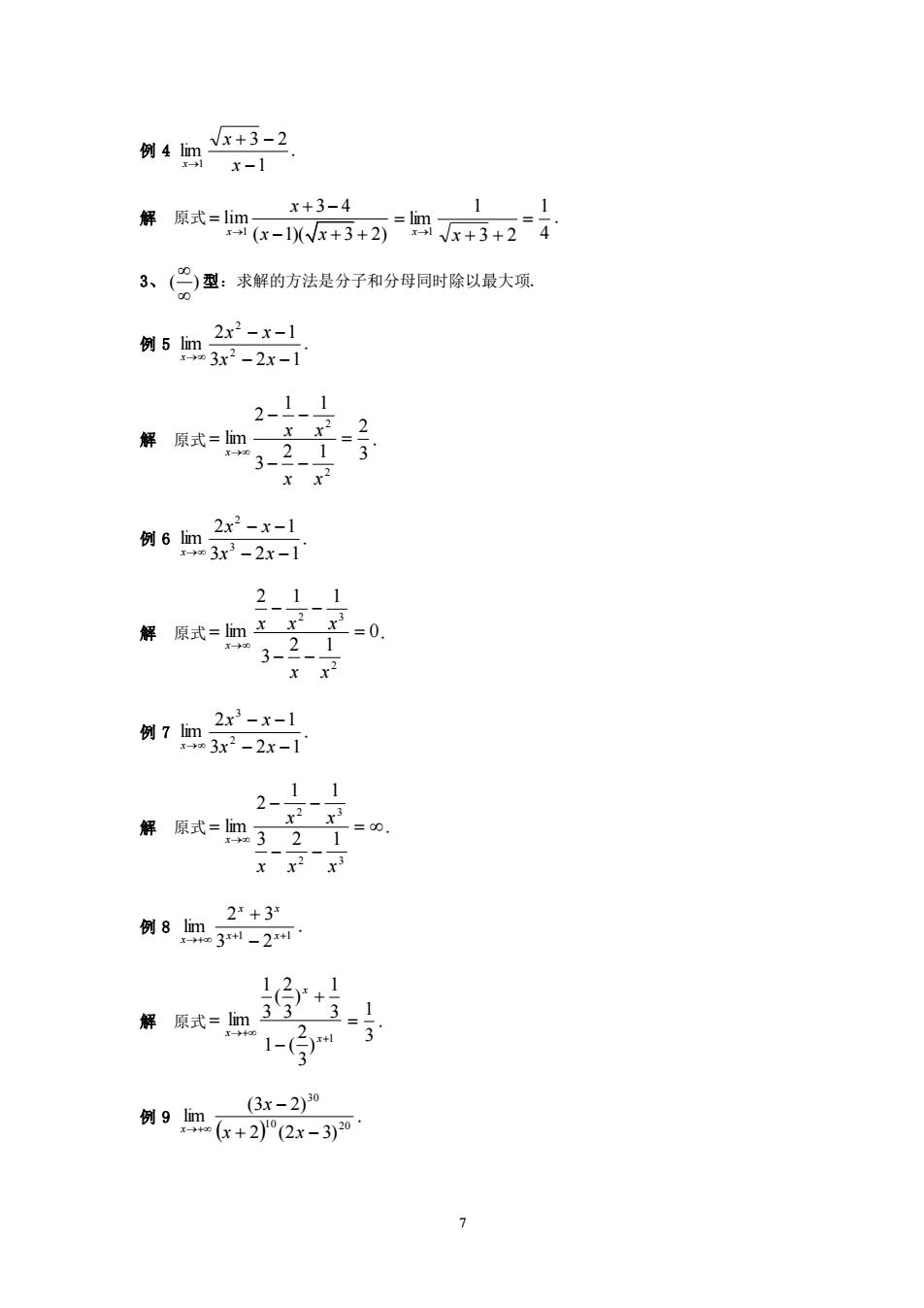
例4卿+3-2 x-1 爆原武=册-W232子 x+3-4 1 3、(份型:求解的方法是分子和分母同时除以最大项 2x2-x-1 例5m3x-2x-1 2-11 x22 x x2 2x2-x-1 例6m3x-2x-1 211 解原式=m士子三=0 3-2 xx 2x3-x-1 例7m3-2x-1 11 2- 2¥+33 例8m3-2 解原式=m 1- (3x-2)0 例9m-+2产2x-3
7 例 4 1 3 2 lim 1 − + − → x x x . 解 原式 1 3 4 lim ( 1)( 3 2) x x → x x + − = − + + 4 1 3 2 1 lim 1 = + + = → x x . 3、 ( ) 型:求解的方法是分子和分母同时除以最大项. 例 5 3 2 1 2 1 lim 2 2 − − − − → x x x x x . 解 原式 3 2 2 1 3 1 1 2 lim 2 2 = − − − − = → x x x x x . 例 6 3 2 1 2 1 lim 3 2 − − − − → x x x x x . 解 原式 0 2 1 3 2 1 1 lim 2 2 3 = − − − − = → x x x x x x . 例 7 3 2 1 2 1 lim 2 3 − − − − → x x x x x . 解 原式 = − − − − = → 2 3 2 3 3 2 1 1 1 2 lim x x x x x x . 例 8 1 1 3 2 2 3 lim + + →+ − + x x x x x . 解 原式 1 ) 3 2 1 ( 3 1 ) 3 2 ( 3 1 lim + →+ − + = x x x 3 1 = . 例 9 ( ) 10 20 30 2 (2 3) (3 2) lim + − − →+ x x x x

3-2)∞ 解原式= 0a 例10m+是++ 1+ 4、(四-0)型:求解的方法是转化为(分或(台.常用的方法有:通分母法和分子有理 化法。 解原动号 x-1 例12m(Wx+F-V) 原式mx+F+G+, 5、(0)型。求解的方法是转化为政.倒 练习题1.3 1.求下列极限: 0-24 @册 )m-2+1 x2-1 ④2+e 3x-1 、x2-3x+2 (6)i四2x+x-10 0 2红号 a0)卿-1 8
8 解 原式 30 10 20 2 (3 ) lim 2 3 (1 ) (2 ) x x x x →+ − = + − 30 20 3 2 = . 例 10 ) 1 2 lim ( 2 2 2 n n n n n + + + → . 解 原式 2 2 1 2 lim n n → n + + + = 2 ( 1) lim n 2 n n → n + = 1 1 1 lim n 2 2 n → + = = . 4、( − )型:求解的方法是转化为 ) 0 0 ( 或 ( ) . 常用的方法有:通分母法和分子有理 化法. 例 11 ) 1 2 1 1 lim ( 2 1 − − x→ x − x . 解 原式= 1 1 lim ( 1)( 1) x x → x x − − + 1 1 1 lim x→ x 1 2 = = + . 例 12 lim ( x x x) n + − →+ . 解 原式= lim x x x x x →+ + + 1 1 lim 2 1 1 1 x x →+ = = + + . 5、( 0 )型:求解的方法是转化为 ) 0 0 ( 或 ( ) .(略) 练习题 1.3 1.求下列极限: (1) 2 2 1 6 5 lim x 3 2 x x → x x + + + + ; (2) 2 1 1 lim x 1 x → x + − ; (3) 2 2 1 2 1 lim x 1 x x → x − + − ; (4) 3 0 2 1 lim( ) 3 1 x x x x e → x − + + − ; (5) 2 2 2 3 2 lim x 2 10 x x → x x − + + − ; (6) 3 2 2 0 3 2 lim x 2 x x x → x x − + + ; (7) 2 2 3 6 9 lim x 4 3 x x → x x − + − + ; (8) 3 2 2 3 lim 2 4 2 1 − + + − → x x x x x ; (9) 2 3 1 2 3 lim x x x →− x x − − − ; (10) 0 1 1 lim x x → x + − ;

aw 2求下列极限: 2x2+3 (2)m7-2x+ @ w-“2 6)ae”+cmx+之》: (3r-2)0 )mx+22x-3驴 x2 8)m2x-2x+ (9)limF(Wx+2-√x+i): 11 1 10)m2+23++7 n-n+ 1.4两个重要极限 1.4.1第一个重要极限 公试回=1. 品得 州1四2 2-细2-号 解原式=m52x 例2gsn2x tan3x 解默=02292 例3im 2m.2sm 帮原式-回于- 168 9
9 (11) 1 2 7 3 lim 3 1 2 x x → x + − + − ; (12) 1 1 lim x 1 x → x + − . 2.求下列极限: (1) 2 2 2 3 lim x 2 3 x x → x x + − + − ; (2) 2 3 2 3 lim x 2 1 x → x x + − + ; (3) 3 2 2 2 lim x 2 1 x x → x x + − − − ; (4) 5 5 ( 2) 3 lim x 2 1 x → x + − − ; (5) 3 1 lim ( arctan ) x x e x x − →+ + + ; (6) 2 1 2 3 lim( 5 ) 2 3 x x x → x − + ; (7) ( ) 30 10 20 (3 2) lim 2 (2 3) x x x x → − + − ; (8) ) 2 1 2 1 lim ( 2 2 3 + − → − x x x x x ; (9) lim ( 2 1) x x x x →+ + − + ; (10) 1 1 1 lim ( ) 1 2 2 3 ( 1) n→+ n n + + + + . 1.4 两个重要极限 1.4.1 第一个重要极限 公式: 1 sin lim 0 = → x x x . 推论: 1 ( ) sin ( ) lim ( ) 0 = → f x f x f x . 例1 0 sin 2 lim x 5 x → x . 解 原式 0 2sin 2 lim x 5 2 x → x = 0 2 sin 2 2 lim 5 2 5 x x → x = = . 例2 0 tan 3 lim x sin 2 x → x . 解 原式 0 3sin 3 2 lim( ) x 3cos3 2 sin 2 x x → x x x = = 0 0 0 3 sin 3 2 1 3 lim lim lim 2 3 sin 2 cos3 2 x x x x x → → → x x x = . 例3 2 0 1 cos 2 lim x x → x − . 解 原式 2 2 0 2sin 4 lim x x → x = = 2 0 2 2sin 1 4 lim 8 16( ) 4 x x → x = .

例4四amr-snx 解原式 mmx.1-c0s·0mx·,x2eos= 1 州5 -lan(π-0=l. 解原式=四红-) 注:公式,巴中1,适用于三角函数与系高数相除的情形,解超的更路是起分号 0f(x) 演化出正弦的角度函数,而后利用公式 1.4.2第二个重要极限 公式:m0+=e. 推论:思+f丙o=e和+=e, 州6回0+经, 解原式=m0+=2 2 例7=+2产 解默-0+红台- 例80-安 集赋=+之r学- 例91im(1-2x)安 解原式=ml+(←2x高a安=e
10 例 4 3 0 tan sin lim x x x x − → . 解 原式 3 0 1) cos 1 sin ( lim x x x x − = → ) cos sin 1 cos 1 lim ( 2 0 x x x x x x − = → 2 2 0 2sin sin 1 2 lim( ) cos 4 4 x x x → x x x = 2 1 = . 例 5 tan lim x x → x − . 解 原式 tan( ) lim 1 ( ) x x x → − − = = − − . 注:公式 1 ( ) sin ( ) lim ( ) 0 = → f x f x f x ,适用于三角函数与幂函数相除的情形,解题的思路是把分母 演化出正弦的角度函数,而后利用公式. 1.4.2 第二个重要极限 公式: e x x x + = → ) 1 lim (1 . 推论: e f x f x f x + = → ( ) ( ) ) ( ) 1 lim (1 和 x e x x + = → 1 0 lim (1 ) . 例 6 2 lim(1 )x x→ x + . 解 原式 2 1 2 2 lim(1 ) 2 x x e x → = + = . 例 7 2 2 lim(1 ) 3 x x→ x + . 解 原式 3 4 2 3 1 lim(1 ) 3 2 x x x → = + 4 3 = e . 例 8 1 1 lim(1 ) 2 x x x + → − . 解 原式 1 1 2 ( ) 2 2 1 lim(1 ) 2 x x x x e x + − − − → = + = − . 例 9 2 3 0 lim(1 2 ) x x x → − . 解 原式 1 2 ( 2 ) 2 3 0 lim[1 ( 2 )] x x x x x − − → = + − 4 3 e − =