
中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 第二章数值微分和数值积分
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 第二章 数值微分和数值积分

中图科亨技术大学数学案 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 数值微分 1.函数fx)以离散点列给出时,而要求我们给出导数值, 2.函数fx过于复杂 这两种情况都要求我们用数值的方法求函数的导数值 微积分中,关于导数的定义如下: a)=丹+f四)-创mx+创f心创 h 10 h h>0 2h 自然,而又简单的方法就是,取极限的近似值,即差商
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 数值微分 h f x h f x h h f x f x h h f x h f x f x h h h 2 ( ) ( ) lim ( ) ( ) lim ( ) ( ) '( ) lim 0 0 0 + − − = − − = + − = → → → 1. 函数f(x)以离散点列给出时,而要求我们给出导数值, 2. 函数f(x)过于复杂 这两种情况都要求我们用数值的方法求函数的导数值 微积分中,关于导数的定义如下: 自然,而又简单的方法就是,取极限的近似值,即差商
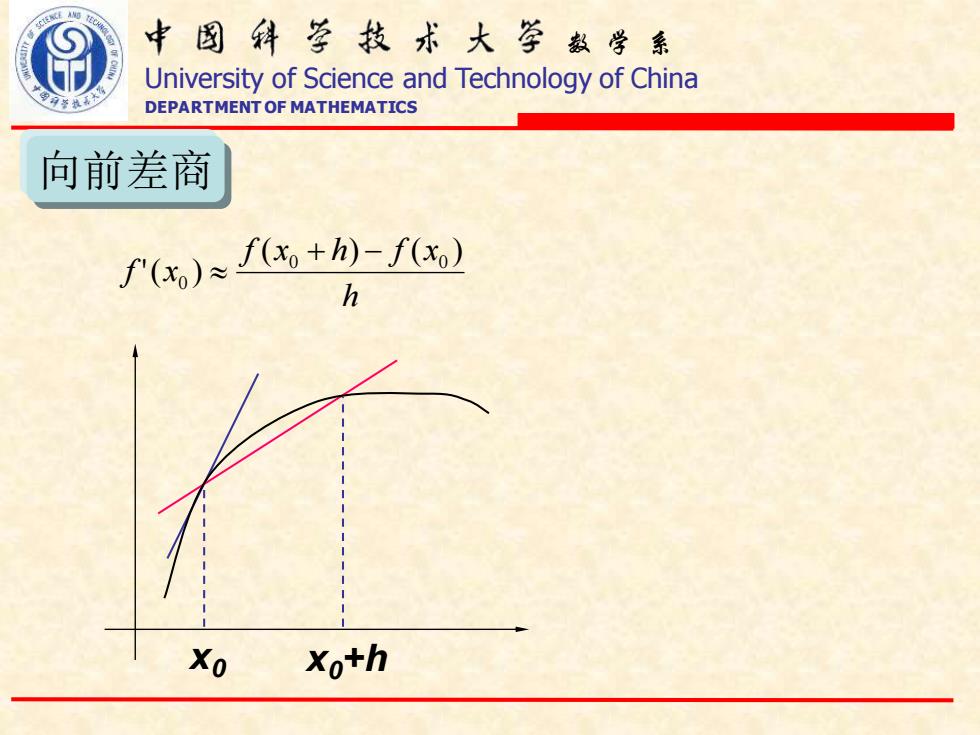
中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 向前差商 f(x)≈f+)-f) h Xo Xo+h
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS h f x h f x f x ( ) ( ) '( ) 0 0 0 + − 向前差商 x0 x0+h

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 由Taylor展开 +粉)+)+空5五+ 因此,有误差 =f)-+的f-=o h
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 由Taylor展开 f x x h h f x + h = f x + hf x + 0 0 + 2 0 0 0 ''( ), 2! ( ) ( ) '( ) 因此,有误差 ''( ) ( ) 2! ( ) ( ) ( ) '( ) 0 0 0 f O h h h f x h f x R x f x = − = + − = −
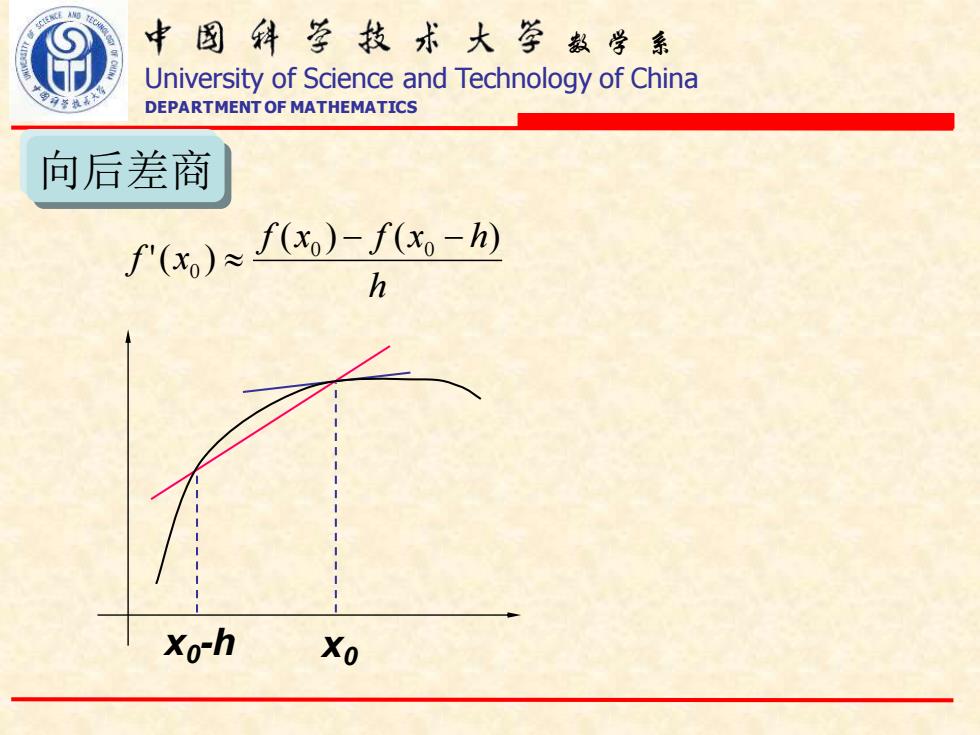
中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 向后差商 f(x,)x)-f。-M h Xo-h Xo
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS h f x f x h f x ( ) ( ) '( ) 0 0 0 − − 向后差商 x0 -h x0

中图 科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 由Taylor展开 6-台rs5s6 因此,有误差 Rx)=f(x)-)-f。-)- h 分5=0
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 由Taylor展开 f x x h h f x − h = f x − hf x + 0 0 + 2 0 0 0 ''( ), 2! ( ) ( ) '( ) 因此,有误差 ''( ) ( ) 2! ( ) ( ) ( ) '( ) 0 0 0 f O h h h f x f x h R x f x = = − − = −
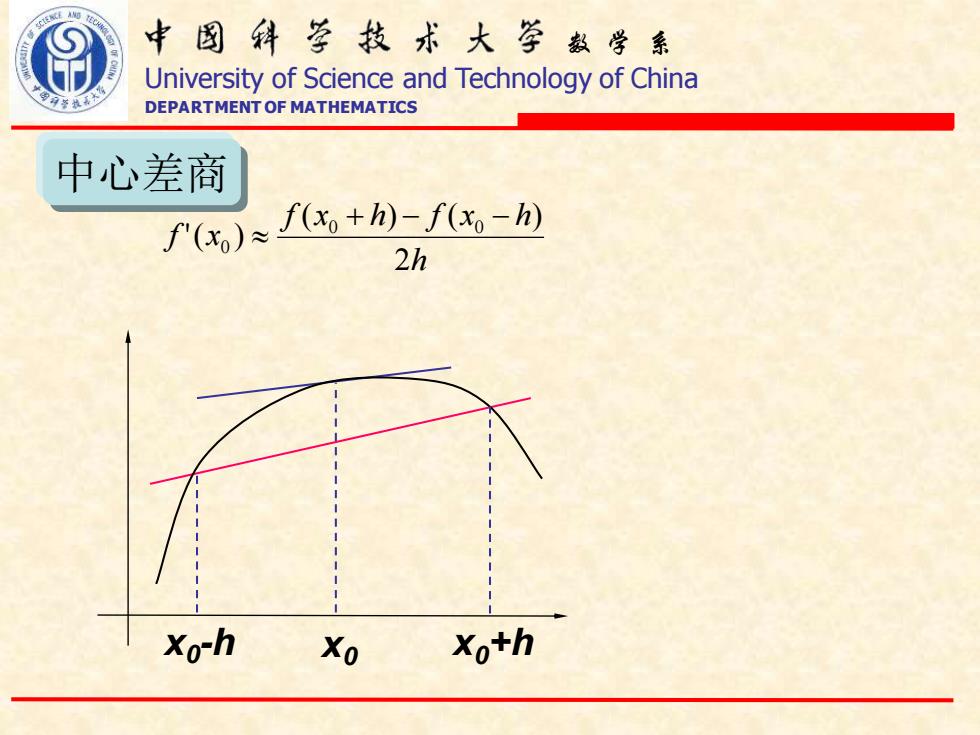
中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 中心差商 f')x+-f-) 2h Xo-h Xo Xo+h
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS h f x h f x h f x 2 ( ) ( ) '( ) 0 0 0 + − − 中心差商 x0 -h x0 x0+h

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 由Taylor)展开 h2 h f(xo+h)=f(xo)+hf'(xo)+ f)+3f(5≤5≤x+h f(x。-h)=f(x)-hf'(x)+ h2 ∫)-35人-h≤5≤x 因此,有误差 Rx)=fx,)-f+0-f。-D 2h -VE)+1传】-严写0=0时) h
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 由Taylor展开 2 3 0 0 0 0 1 0 1 0 2 3 0 0 0 0 2 0 2 0 ( ) ( ) '( ) ''( ) '''( ), 2! 3! ( ) ( ) '( ) ''( ) '''( ), 2! 3! h h f x h f x hf x f x f x x h h h f x h f x hf x f x f x h x + = + + + + − = − + − − 因此,有误差 '''( ) ( ) 6 [ '''( ) '''( )] 12 2 ( ) ( ) ( ) '( ) 2 2 1 2 2 0 0 0 f O h h f f h h f x h f x h R x f x = + = = + − − = −
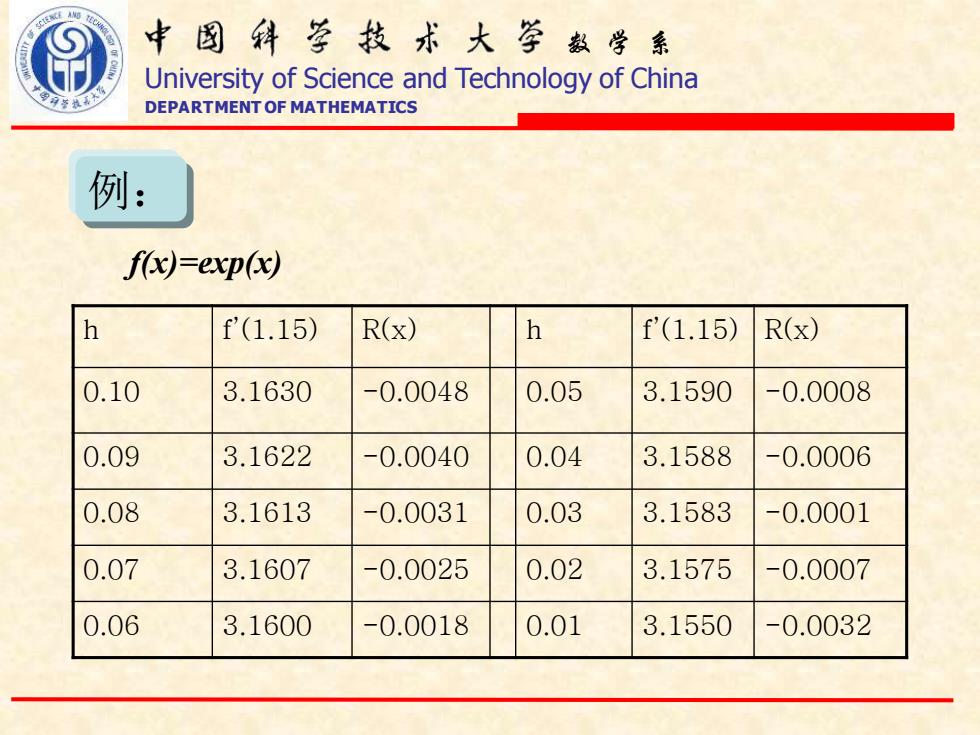
中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 例: f(x)-exp(x) h f'(1.15) R(x) h f'(1.15) R(x) 0.10 3.1630 -0.0048 0.05 3.1590 -0.0008 0.09 3.1622 -0.0040 0.04 3.1588 -0.0006 0.08 3.1613 -0.0031 0.03 3.1583 -0.0001 0.07 3.1607 -0.0025 0.02 3.1575 -0.0007 0.06 3.1600 -0.0018 0.01 3.1550 -0.0032
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS f(x)=exp(x) h f’(1.15) R(x) h f’(1.15) R(x) 0.10 3.1630 -0.0048 0.05 3.1590 -0.0008 0.09 3.1622 -0.0040 0.04 3.1588 -0.0006 0.08 3.1613 -0.0031 0.03 3.1583 -0.0001 0.07 3.1607 -0.0025 0.02 3.1575 -0.0007 0.06 3.1600 -0.0018 0.01 3.1550 -0.0032 例:

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 由误差表达式,越小,误差越小,但同时舍入误差增大, 所以,有个最佳步长 我们可以用事后误差估计的方法来确定 设D(h),D(h/2)分别为步长为h,h/2的差商公式。则 D-D吃sc 时的步长/2就是合适的步长 f(x)-D(h)=O(h) f'(x)-D(h) O(h) ≈2 f'(x)-D(h/2)=O(h/2) f'(x)-Dh12) O(h12) f'(x)-D(h)=2f'(x)-2D(h/2) f'(x)-D(h/2)=D(h)-D(h/2)
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 由误差表达式,h越小,误差越小,但同时舍入误差增大, 所以,有个最佳步长 我们可以用事后误差估计的方法来确定 设D(h),D(h/2) 分别为步长为h,h/2 的差商公式。则 − ) 2 ( ) ( h D h D 时的步长h/2 就是合适的步长 '( ) ( ) ( ) '( ) ( / 2) ( / 2) f x D h O h f x D h O h − = − = '( ) ( ) ( ) 2 '( ) ( / 2) ( / 2) f x D h O h f x D h O h − = − f x D h f x D h '( ) ( ) 2 '( ) 2 ( / 2) − = − f x D h D h D h '( ) ( / 2) ( ) ( / 2) − = −