
中国科学技术大学 2002一2003学年第二学期考试试卷 考试科目:概率论与数理统计 得分: 学生所在系: 姓名 学号: (考期:2003年6月30日,闭卷,可用计算器) 一、考虑如图所示的电路图: A 其中开关A、B、C、D、E是独立工作的,每个开关以概率p开着,以概率q-Ip 关着,求一个输入的信号在输出处被接收到的概率:如果一个信号被接收到,那么 开关E是开着的条件概率是多少? 二、设(X,Y的联合密度函数为: fc0=608 其中8是未知参数,-o<日<0。 (1)试求8的极大似然估计©和矩估计a: (2)求常数c1和c2,使得c10-c2为0的无偏估计: (3)求常数c3和c4,使得c30-c4为8的无偏估计: (4)在均方误差意义下比较这两个无偏估计哪个更优。(注:上述常数可与n有关) 五、据信有一种疾病会导致病人的白细胞数目较常人少,假设正常人白细胞数服从均值 为7250(单位:个/位方毫米,下同)的正态分布,现有16个病人,其白细胞的样 本均值为4767,样本标准差为3204,根据这批数据能否认为这种疾病使白细胞数
ѣള〇ᆜᢶᵥཝᆜ 2002—2003 ᆜᒪㅢӂᆜᵕ㘹䈋䈋ভ 㘳䈅、ⴞ˖ᾲ⦷䇪оᮠ⨶㔏䇑 ᗇ ࠶ ˖ ᆖ⭏ᡰ൘㌫˖ ဃ ᆖ ਧ˖ ˄㘳ᵏ˖2003 ᒤ 6 ᴸ 30 ᰕˈ䰝ধˈਟ⭘䇑㇇ಘ˅ аǃ㘳㲁ྲമᡰ⽪Ⲵ⭥䐟മ˖ ަѝᔰޣ AǃBǃCǃDǃE ᱟ⤜・ᐕⲴˈ⇿њᔰޣԕᾲ⦷ p ᔰ⵰ˈԕᾲ⦷ q=1-p ޣ≳ˈ⵰ањ䗃ޕⲴؑਧ൘䗃ࠪ༴㻛᧕᭦ࡠⲴᾲ⦷˗ྲ᷌ањؑਧ㻛᧕᭦ࡠˈ䛓Ѹ ᔰޣ E ᱟᔰ⵰ⲴᶑԦᾲ⦷ᱟཊቁ˛ Ҽǃ䇮(ܺ, ܻ)Ⲵ㚄ਸᇶᓖ࠭ᮠѪ˖ ൜ = (ݕ ,ݔ)݂ ;1 0, ݔ > |ݕ| ,ܿ ݏݎ݄݁ݐ ,0 ≲(1)ᑨᮠ C Ⲵ٬˗(2)ᶑԦᇶᓖ࠭ᮠ݂|(ݔ|ݕ(৺݂|(ݕ|ݔ)˗(3)䇘䇪 X о Y Ⲵ⤜・ ᙗ઼ޣᙗDŽ йǃ൘аᇦ؍䲙ޜਨ䟼ᴹ 10000 њӪ৲؍࣐䲙ˈ⇿Ӫ⇿ᒤԈ 12 ؍ݳ䲙䍩ˈ൘аᒤа њӪ↫ӑⲴᾲ⦷Ѫ 0.006ˈ↫ӑᰦަᇦਟੁ؍䲙ޜਨ亶ਆ 1000 ݳⲴ؍䲙䠁ˈ䰞˖ (1) ؍䲙ޜਨҿᵜⲴᾲ⦷ཊབྷ˛ (2) ؍䲙ޜਨаᒤⲴ࡙⏖нቁҾ 40000 ݳǃ60000 ݳⲴᾲ⦷ཊབྷ˛ ഋǃ䇮( , , , ) X1 X 2 " X n ᱟӾᙫփ X ѝᣭਆⲴањㆰঅ䲿ᵪṧᵜˈᐢ⸕ X Ⲵᾲ⦷ᇶᓖ࠭ ᮠѪ˖ ൜ = (ݔ)݂ ݁ି(௫ିఏ) ;ߠ < ݔ , ݏݎ݄݁ݐ ,0 ަѝߠᱟᵚ⸕৲ᮠˈെλ < Ʌ < λDŽ (1) 䈅≲ߠⲴᶱབྷլ❦ՠ䇑ߠՠ⸙઼䇑ߠ˗෨ (2) ≲ᑨᮠܿଵ઼ܿଶˈ֯ᗇܿଵߠ െ ܿଶѪߠⲴᰐٿՠ䇑˗ (3) ≲ᑨᮠܿଷ઼ܿସˈ֯ᗇܿଷߠ ෨െ ܿସѪߠⲴᰐٿՠ䇑˗ (4) ൘൷ᯩ䈟ᐞѹл∄䖳䘉єњᰐٿՠ䇑ଚњᴤՈDŽ˄⌘˖к䘠ᑨᮠਟо n ᴹޣ˅ ӄǃᦞؑᴹа⿽⯮⯵Պሬ㠤⯵ӪⲴⲭ㓶㜎ᮠⴞ䖳ᑨӪቁˈۇٴ䇮↓ᑨӪⲭ㓶㜎ᮠᴽӾ൷٬ Ѫ 7250˄অս˖њ/・ᯩ∛㊣ˈл਼˅Ⲵ↓ᘱ࠶ᐳˈ⧠ᴹ 16 њ⯵Ӫˈަⲭ㓶㜎Ⲵṧ ᵜ൷٬Ѫ 4767ˈṧᵜḷ߶ᐞѪ 3204ˈṩᦞ䘉ᢩᮠᦞ㜭䇔Ѫ䘉⿽⯮⯵֯ⲭ㓶㜎ᮠ A C B D E
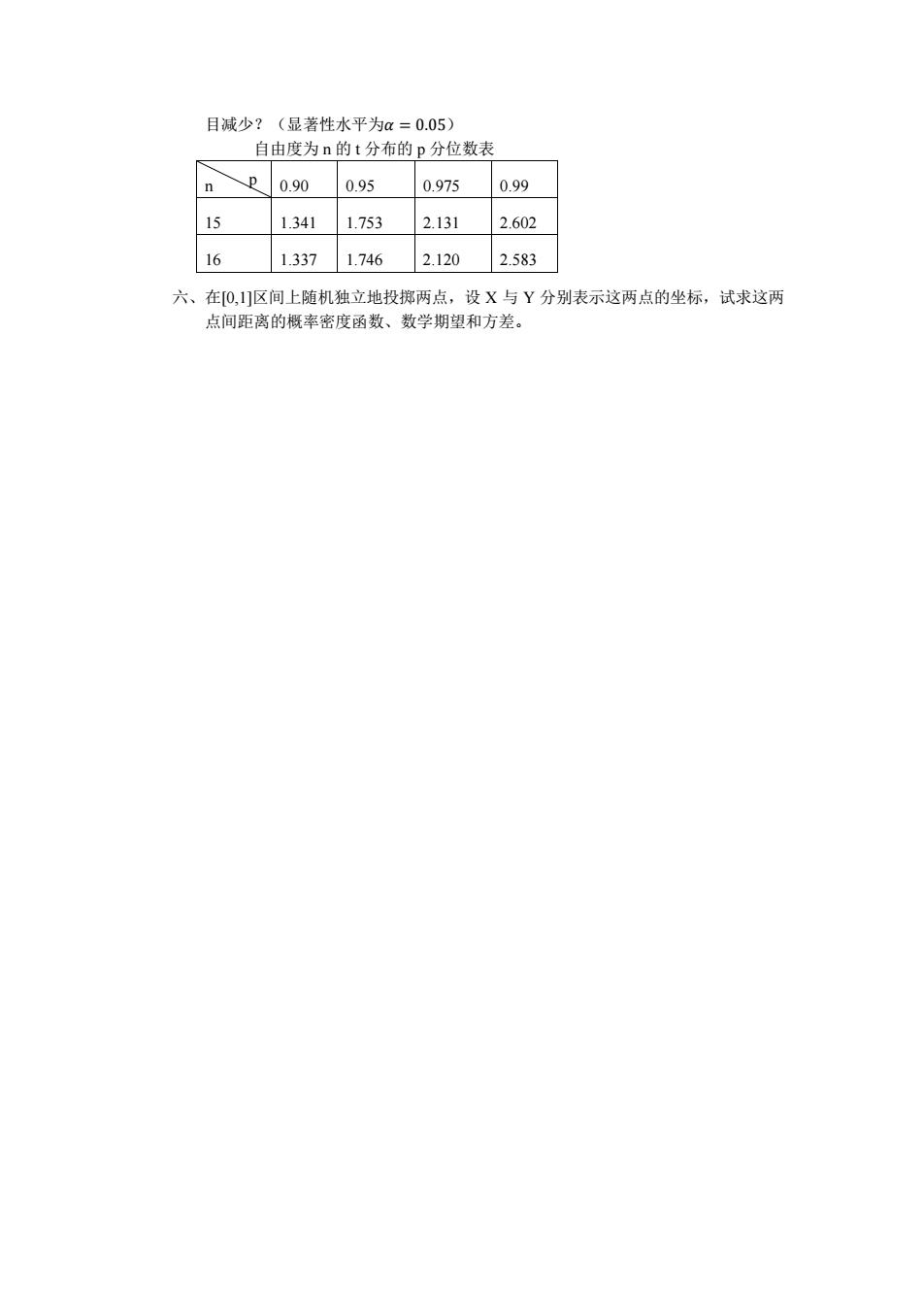
目减少?(显著性水平为a=0.05) 自由度为n的t分布的p分位数表 n0.90 0.95 0.975 0.99 151.3411.7532.1312.602 1613371.7462.1202.583 六、在0,]区间上随机独立地投掷两点,设X与Y分别表示这两点的坐标,试求这两 点间距离的概率密度函数、数学期望和方差
p ⴞ߿ቁ˛˄ᱮ㪇ᙗ≤ᒣѪߙ = 0.05˅ 㠚⭡ᓖѪ n Ⲵ t ࠶ᐳⲴ p ࠶սᮠ㺘 n 0.90 0.95 0.975 0.99 15 1.341 1.753 2.131 2.602 16 1.337 1.746 2.120 2.583 ޝǃ൘[0,1]४䰤к䲿ᵪ⤜・ൠᣅ᧧є⛩ˈ䇮 X о Y ࡛࠶㺘⽪䘉є⛩Ⲵḷˈ䈅≲䘉є ⛩䰤䐍Ⲵᾲ⦷ᇶᓖ࠭ᮠǃᮠᆖᵏᵋ઼ᯩᐞDŽ

中国科学技术大学 2003一2004学年第一学期考试试卷 考试科目:概率论与数理统计 得分: 学生所在系: 姓名 学号: (考期:2004年1月8日,闭卷,可用计算器 一、甲、乙、丙三人独立地向靶子各射击一次,其命中率分别为0.6、0.5和0.4,现已知 恰有两人命中靶子,问: (1)此两人中包括丙的可能性大,还是不包括丙的可能性大? (2)此两人中包括乙的可能性大,还是包括丙的可能性大?(要求写出计算过程〉 二、某种商品一周的需求量是个随机变量,其概率密度为: fo=6e8 各周的需求量相互独立,试求 (1)两周需求量的概率密度: (2)三周需求量的概率密度。 三、利用中心极限定理求解: (1)设计算机在进行加法运算时,每次取整的误差相互独立,且服从0.5,0.5]止的均 匀分布,若婴保证误差总和的绝对值不超过20的概率大于或者等于095,问至多只 能进行多少次加法运算? (2)lmnm张-oe-n=2 四、设样本(X1,X2,.,X)抽自总体x~fx;),其中: fx:9)=e号,x>9:0eR) (1)试求8的矩估计6和极大似然估计': (2)验证和日是否为9的无偏估计,若不是无偏估计,试将其分别修正为无偏估 计0,和02 (3)比较a1和2何者为优? 五、为考察钢铁工人和电厂工人平均工资的差别,从两厂各抽取若干工人调查,结果如 下 钢厂:74.65,72,69(元) 电厂:75,7874,76,72(元) 若钢厂工人与电厂工人工资分别服从正态分布N(4,)与N(2,),总体独立且均 值方差未知,试据上述数据判断: (1)是否可以认为a=经?(a=0.05) (2)钢铁工人平均工资是否低于电厂工人平均工资?(a=0.05)
ѣള〇ᆜᢶᵥཝᆜ 2003—2004 ᆜᒪㅢжᆜᵕ㘹䈋䈋ভ 㘳䈅、ⴞ˖ᾲ⦷䇪оᮠ⨶㔏䇑 ᗇ ࠶ ˖ ᆖ⭏ᡰ൘㌫˖ ဃ ᆖ ਧ˖ ˄㘳ᵏ˖2004 ᒤ 1 ᴸ 8 ᰕˈ䰝ধˈਟ⭘䇑㇇ಘ˅ аǃ⭢ǃ҉ǃщйӪ⤜・ൠੁ䶦ᆀሴࠫа⅑ˈަભѝ⦷࡛࠶Ѫ 0.6ǃ0.5 ઼ 0.4.⧠ᐢ⸕ ᚠᴹєӪભѝ䶦ᆀˈ䰞˖ ˄1˅↔єӪѝवᤜщⲴਟ㜭ᙗབྷˈ䘈ᱟнवᤜщⲴਟ㜭ᙗབྷ˛ ˄2˅↔єӪѝवᤜ҉Ⲵਟ㜭ᙗབྷˈ䘈ᱟवᤜщⲴਟ㜭ᙗབྷ˛˄㾱≲߉ࠪ䇑㇇䗷〻˅ ҼǃḀ⿽୶૱аઘⲴ䴰≲䟿ᱟњ䲿ᵪਈ䟿ˈަᾲ⦷ᇶᓖѪ˖ ൜ = (ݐ)݂ 0 > ݐ,௧݁ିݐ 0, ݐ 0 ઘⲴ䴰≲䟿ӂ⤜・ˈ䈅≲˖ ˄1˅ єઘ䴰≲䟿Ⲵᾲ⦷ᇶᓖ˗ ˄2˅ йઘ䴰≲䟿Ⲵᾲ⦷ᇶᓖDŽ йǃ࡙⭘ѝᗳᶱ䲀ᇊ⨶≲䀓˖ ˄1˅䇮䇑㇇ᵪ൘䘋㹼࣐⌅䘀㇇ᰦˈ⇿⅑ਆᮤⲴ䈟ᐞӂ⤜・ˈфᴽӾ[-0.5,0.5]кⲴ൷ र࠶ᐳˈ㤕㾱؍䇱䈟ᐞᙫ઼Ⲵ㔍ሩ٬н䎵䗷 20 Ⲵᾲ⦷བྷҾᡆ㘵ㅹҾ 0.95ˈ䰞㠣ཊਚ 㜭䘋㹼ཊቁ⅑࣐⌅䘀㇇˛ ˄2˅ ݈݅݉՜ஶ σ ೖ ! ݁ି =? ୀ ഋǃ䇮ṧᵜ( , , , ) X1 X 2 " X n ᣭ㠚ᙫփܺ~݂(ݔ ;ߠަˈ(ѝ˖ ଵ) = ߠ ;ݔ)݂ ଶ ݁ିೣషഇ (ܴ א ߠ ;ߠ < ݔ) , మ ˄1˅ 䈅≲ߠⲴ⸙ՠ䇑ߠ઼ᶱབྷլ❦ՠ䇑כߠ ˗ כߠ઼ߠ傼䇱˅ 2˄ ᱟѪߠⲴᰐٿՠ䇑ˈ㤕нᱟᰐٿՠ䇑ˈ䈅ሶަ؞࡛࠶↓Ѫᰐٿՠ ߠ䇑 ߠ઼ଵ ଶ˗ ˄3˅ ∄䖳ߠ ߠ઼ଵ ଶօ㘵ѪՈ˛ ӄǃѪ㘳ሏ䫒䫱ᐕӪ઼⭥লᐕӪᒣ൷ᐕ䍴Ⲵᐞ࡛ˈӾєলᣭਆ㤕ᒢᐕӪ䈳ḕˈ㔃᷌ྲ л˖ 䫒ল˖74ˈ65ˈ72ˈ69˄ݳ˅ ⭥ল˖75ˈ78ˈ74ˈ76ˈ72˄ݳ˅ 㤕䫒লᐕӪо⭥লᐕӪᐕ䍴࡛࠶ᴽӾ↓ᘱ࠶ᐳܰ(ߤଵ, ߪଵ ଶ)оܰ(ߤଶ, ߪଶ ଶ)ˈᙫփ⤜・ф൷ ٬ᯩᐞᵚ⸕ˈ䈅ᦞк䘠ᮠᦞࡔ˖ᯝ ˄1˅ ᱟਟԕ䇔Ѫߪଵ ଶ = ߪଶ ଶ˛˄ߙ = 0.05˅ ˄2˅ 䫒䫱ᐕӪᒣ൷ᐕ䍴ᱟվҾ⭥লᐕӪᒣ൷ᐕ䍴˛˄ߙ = 0.05˅

中国科学技术大学 2003一2004学年第二学期考试试卷 考试科目:概率论与数理统计 得分: 学生所在系: 姓名」 学号: (考期:2004年6月25日,闭卷,可用计算器) 一、判断和填空: (1)设PA)=0,则A为不可能事件。 (2)设XY)服从二元正态,Cov(X.Y0,则X、Y相互独立。 (3)设X、Y相互独立,则X、Y的联合分布可以由X和Y的边缘分布唯一确 定。 (4)设X1,.,Xn为从同一个总体中抽取的一个样本,则max(X,Xn) mim(X1,.,Xn)+3是统计量。 (5)设0>0,X的概率分布函数为: 0 x5u 则随机变量X的密度函数为()。 (6)设X、Y服从单位圆x2+y2≤1上的均匀分布,则在给定Y0.5条件下的 X的条件密度函数为()。 (7)设X和Y相互独立,它们的均值全为0,方差全为1,记V=XY,则X与 V的相关系数为() 二、求:(1)PX=2X=):(2X2+Y2的分布,其中X、Y的联合分布如下: -1 0 1 2 0.120.080.30 0.15 1 0.080.22 0 0.05 三、设X服从期望为2的指数分布,Y服从(0,1)上的均匀分布,且X与Y相互独立, 求:(1)X-Y的概率密度函数:(2)PX<Y)。 四、桌上有三个盒子,在甲盒中装有2支红芯圆珠笔,4支蓝芯圆珠笔,乙盒中装有 支红芯圆珠笔,2支蓝芯圆珠笔,丙盒中装有3支红芯圆珠笔,3支蓝芯圆珠笔 今从三个盒子中任取一支笔,设甲乙丙三盒取笔的概率相等。试求: (1)取得红笔的概率:(2)在已知取得红笔的条件下,问笔从哪个盒子中取出的概 率最大? 五、某工厂生产线甲根据专利生产灯泡,生产线乙根据本厂原有技术生产。现分别在生 产线甲和乙两条生产线各抽取8个灯泡,测得其寿命分别为(千小时): 对生产线甲:10,9,3,11,5,7,9,11: 对生产线乙:4,9,6,5,3,5,7,7: 设灯泡寿命服从正态分布,且方差相等。试分别在显著性水平a=0.05和a=0.01下 检验生产线甲的灯泡是否比生产线乙生产的寿命要长
Y ѣള〇ᆜᢶᵥཝᆜ 2003—2004 ᆜᒪㅢӂᆜᵕ㘹䈋䈋ভ 㘳䈅、ⴞ˖ᾲ⦷䇪оᮠ⨶㔏䇑 ᗇ ࠶ ˖ ᆖ⭏ᡰ൘㌫˖ ဃ ᆖ ਧ˖ ˄㘳ᵏ˖2004 ᒤ 6 ᴸ 25 ᰕˈ䰝ধˈਟ⭘䇑㇇ಘ˅ аǃࡔ઼ᯝປオ˖ ˄1˅ 䇮 P(A)=0ˈࡉ A Ѫнਟ㜭һԦDŽ ˄2˅ 䇮(X,Y)ᴽӾҼݳ↓ᘱˈCov(X,Y)=0,ࡉ XǃY ӂ⤜・DŽ ˄3˅ 䇮 XǃY ӂ⤜・ˈࡉ XǃY Ⲵ㚄ਸ࠶ᐳਟԕ⭡ X ઼ Y Ⲵ䗩㕈࠶ᐳୟа⺞ ᇊDŽ ˄4˅ 䇮ܺଵ, ڮ ܺ, ѪӾ਼ањᙫփѝᣭਆⲴањṧᵜˈࡉܽ݉ݔܺ)ଵ, ڮ (ܺ, െ ݉݅݊(ܺଵ, ڮ+(ܺ, 3 ᱟ㔏䇑䟿DŽ ˄5˅ 䇮Ʌ > 0ˈX Ⲵᾲ⦷࠶ᐳ࠭ᮠѪ˖ ൝ = (ݔ)ܨ 1 െ ݁ݔ ቄെ ݔ െ ߤ ቅ ߠ ߤ > ݔ , 0 ߤ ݔ , ࡉ䲿ᵪਈ䟿 X Ⲵᇶᓖ࠭ᮠѪ˄˅DŽ ˄6˅ 䇮 XǃY ᴽӾঅսശݔଶ + ݕଶ 1кⲴ൷र࠶ᐳˈࡉ൘㔉ᇊ Y=0.5 ᶑԦлⲴ X ⲴᶑԦᇶᓖ࠭ᮠѪ˄˅DŽ ˄7˅ 䇮 X ઼ Y ӂ⤜・ˈᆳԜⲴ൷٬ޘѪ 0ˈᯩᐞޘѪ 1ˈ䇠 V=X-Yˈࡉ X о V Ⲵޣ㌫ᮠѪ˄˅DŽ Ҽǃ≲˖˄1˅P(Y=2|X=1)˗(2)ܺଶ + ܻଶⲴ࠶ᐳˈަѝ XǃY Ⲵ㚄ਸ࠶ᐳྲл˖ X -1 0 1 2 -1 0.12 0.08 0.30 0.15 1 0.08 0.22 0 0.05 йǃ䇮 X ᴽӾᵏᵋѪ 2 Ⲵᤷᮠ࠶ᐳˈY ᴽӾ(0,1)кⲴ൷र࠶ᐳˈф X о Y ӂ⤜・ˈ ≲˖˄1˅X-Y Ⲵᾲ⦷ᇶᓖ࠭ᮠ˗˄2˅P(X<Y)DŽ ഋǃṼкᴹйњⴂᆀˈ൘⭢ⴂѝ㻵ᴹ 2 ᭟㓒㣟ശ⨐ㅄˈ4 ᭟㬍㣟ശ⨐ㅄˈ҉ⴂѝ㻵ᴹ 4 ᭟㓒㣟ശ⨐ㅄˈ2 ᭟㬍㣟ശ⨐ㅄˈщⴂѝ㻵ᴹ 3 ᭟㓒㣟ശ⨐ㅄˈ3 ᭟㬍㣟ശ⨐ㅄˈ ӺӾйњⴂᆀѝԫਆа᭟ㅄˈ䇮⭢҉щйⴂਆㅄⲴᾲ⦷ㅹDŽ䈅≲˖ ˄1˅ਆᗇ㓒ㅄⲴᾲ⦷˗˄2˅൘ᐢ⸕ਆᗇ㓒ㅄⲴᶑԦлˈ䰞ㅄӾଚњⴂᆀѝਆࠪⲴᾲ ⦷ᴰབྷ˛ ӄǃḀᐕল⭏ӗ㓯⭢ṩᦞу࡙⭏ӗ⚟⌑ˈ⭏ӗ㓯҉ṩᦞᵜলᴹᢰᵟ⭏ӗDŽ⧠࡛࠶⭏൘ ӗ㓯⭢઼҉єᶑ⭏ӗ㓯ᣭਆ 8 њ⚟⌑ˈ⍻ᗇަሯભ࡛࠶Ѫ˄ॳሿᰦ˅˖ ሩ⭏ӗ㓯⭢˖10ˈ9ˈ3ˈ11ˈ5ˈ7ˈ9ˈ11˗ ሩ⭏ӗ㓯҉˖4ˈ9ˈ6ˈ5ˈ3ˈ5ˈ7ˈ7˗ 䇮⚟⌑ሯભᴽӾ↓ᘱ࠶ᐳˈфᯩᐞㅹDŽ䈅࡛࠶൘ᱮ㪇ᙗ≤ᒣߙ = 0.05઼ߙ = 0.01л Ự傼⭏ӗ㓯⭢Ⲵ⚟⌑ᱟ∄⭏ӗ㓯҉⭏ӗⲴሯભ㾱䮯DŽ

六、设总体X服从(1,日+1)上的均匀分布,X,Xn为总体X中抽取的一个样本。试求: (1)求8的矩估计1和极大似然估计©2: (2)A,和A2是否为9的无偏估计,若不是,请加以修正: (3)A,=28。-2是0的无偏估计,其中A。=2+W4+t2,问,的修正(如果需 n+ 要修正的话)和3哪个更有效?
ޝǃ䇮ᙫփ X ᴽӾ(1, ߠ + 1)кⲴ൷र࠶ᐳˈܺଵ, ڮܺ, Ѫᙫփ X ѝᣭਆⲴањṧᵜDŽ䈅≲˖ ˄1˅≲ߠⲴ⸙ՠ䇑ߠ ଵ઼ᶱབྷլ❦ՠ䇑ߠ ଶ˗ ߠ˅2 ˄ ߠ઼ଵ ଶᱟѪߠⲴᰐٿՠ䇑ˈ㤕нᱟˈ䈧࣐ԕ؞˗↓ ߠ˅3 ˄ ଷ = 2ߠ ସ െ 2ᱟߠⲴᰐٿՠ䇑ˈަѝߠ ସ = ଶభାమశڮାషభାଶ ାଶ ˈ䰞ߠ ଵⲴ؞᷌ྲ˄↓䴰 ߠ઼˅Ⲵ䈍↓؞㾱 ଷଚњᴤᴹ᭸˛

中国科学技术大学 2004一2005学年第一学期考试试卷 考试科目:概率论与数理统计 得分: 学生所在系: 姓名 学号: (考期:2005年1月20日,闭卷,可用计算器) 一、甲、乙、丙三门火炮同时独立地向目标射击,其命中率分别为02,0.3和0.5。目 标被命中一发而被推毁的概率为0.2,被命中两发而被摧毁的概率为0.6,被命中三 发而被摧毁的概率0.9,试求: (1)三门火炮在一次射击中摧毁目标的概率: (2)在目标被摧毁的条件下,其只由甲火炮击中的概率。 二、设X与Y独立同分布,都服从参数为的指数分布,试求Z的分布密度,其中: (1)Z=min{X.Y) (2)Z=X+Y。 三、将一枚骰子独立地投掷n次,令X与Y分别表示其1点出现的次数和6点出现的 次数,并记Z=n-X。试求: (1)X与Y的协方差及相关系数: (2)X与Z的相关系数。 四、设样本X,Xn抽自总体X,总体的密度为: X-x0)=层e学,x之4:,其中0,R为未知参数,>0为已知数。 0 x< (1)求8,的矩估计a,和极大似然估计8: (2)百,和0:是否为0,的无偏估计?是加以证明,不是请加以修正为无偏估计量。 五、某校组织学生参加英文词汇训练,并在年初与年底(即训练前与训后)各举行一次 阅读考试,以考察训练的效果。现随机抽取10名同学,将其年初与年底的考试成 绩记录如下: 学生 12345678910 年初成绩64438472529377586991 年底成绩72508680509078577295 假定两次考分之差服从正态分布,试由此判断词汇训练是否有显著效果?(分别在 a=0.05与a=0.01的水平下检验) 六、为了研究色官是否与性别有关,随机抽取1000人进行调查,结果如下 男 女 和 正常 442 514 956
ѣള〇ᆜᢶᵥཝᆜ 2004—2005 ᆜᒪㅢжᆜᵕ㘹䈋䈋ভ 㘳䈅、ⴞ˖ᾲ⦷䇪оᮠ⨶㔏䇑 ᗇ ࠶ ˖ ᆖ⭏ᡰ൘㌫˖ ဃ ᆖ ਧ˖ ˄㘳ᵏ˖2005 ᒤ 1 ᴸ 20 ᰕˈ䰝ধˈਟ⭘䇑㇇ಘ˅ аǃ⭢ǃ҉ǃщй䰘⚛⛞਼ᰦ⤜・ൠੁⴞḷሴࠫˈަભѝ⦷࡛࠶Ѫ 0.2ˈ0.3 ઼ 0.5DŽⴞ ḷ㻛ભѝаਁ㘼㻛᪗⇱Ⲵᾲ⦷Ѫ 0.2ˈ㻛ભѝєਁ㘼㻛᪗⇱Ⲵᾲ⦷Ѫ 0.6ˈ㻛ભѝй ਁ㘼㻛᪗⇱Ⲵᾲ⦷ 0.9ˈ䈅≲˖ ˄1˅й䰘⚛⛞൘а⅑ሴࠫѝ᪗⇱ⴞḷⲴᾲ⦷˗ ˄2˅൘ⴞḷ㻛᪗⇱ⲴᶑԦлˈަਚ⭡⭢⚛⛞ࠫѝⲴᾲ⦷DŽ Ҽǃ䇮 X о Y ⤜・਼࠶ᐳˈ䜭ᴽӾ৲ᮠѪߣⲴᤷᮠ࠶ᐳˈ䈅≲ Z Ⲵ࠶ᐳᇶᓖˈަѝ˖ ˄1˅Z=min{X,Y}˗ ˄2˅Z=X+YDŽ йǃሶа᷊僠ᆀ⤜・ൠᣅ᧧ n ⅑ˈԔ X о Y ࡛࠶㺘⽪ަ 1 ⛩ࠪ⧠Ⲵ⅑ᮠ઼ 6 ⛩ࠪ⧠Ⲵ ⅑ᮠˈᒦ䇠 Z=n-XDŽ䈅≲˖ ˄1˅X о Y Ⲵॿᯩᐞ৺ޣ㌫ᮠ˗ ˄2˅X о Z Ⲵޣ㌫ᮠDŽ ഋǃ䇮ṧᵜܺଵ, ڮܺ , ᣭ㠚ᙫփ XˈᙫփⲴᇶᓖѪ˖ X~f(ݔ ;ߠଵ) = ൝ ଵ ఏమ ݁ ିೣషഇభ ଵߠ ݔ , ഇమ ଵߠ > ݔ ,0 ˈަѝߠଵ אܴ Ѫᵚ⸕৲ᮠˈߠଶ > 0Ѫᐢ⸕ᮠDŽ ˄1˅ ≲ߠଵⲴ⸙ՠ䇑ߠ ଵ઼ᶱབྷլ❦ՠ䇑ߠଵ ˗כ ߠ ˅2˄ ଵ઼ߠଵ כ ᱟѪߠଵⲴᰐٿՠ䇑˛ᱟ࣐ԕ䇱᰾ˈнᱟ䈧࣐ԕ؞↓Ѫᰐٿՠ䇑䟿DŽ ӄǃḀṑ㓴㓷ᆖ⭏৲࣐㤡᮷䇽≷䇝㓳ˈᒦ൘ᒤࡍоᒤᓅ˄ণ䇝㓳ࡽо䇝ਾ˅Ѯ㹼а⅑ 䰵䈫㘳䈅ˈԕ㘳ሏ䇝㓳Ⲵ᭸᷌DŽ⧠䲿ᵪᣭਆ 10 ਼ᆖˈሶަᒤࡍоᒤᓅⲴ㘳䈅ᡀ 㔙䇠ᖅྲл˖ ۇٴᇊє⅑㘳࠶ѻᐞᴽӾ↓ᘱ࠶ᐳˈ䈅⭡↔ࡔᯝ䇽≷䇝㓳ᱟᴹᱮ㪇᭸᷌˛˄࡛࠶൘ ߙ = 0.05оߙ = 0.01Ⲵ≤ᒣлỰ傼˅ ޝǃѪҶ⹄ウ㢢ⴢᱟоᙗ࡛ᴹޣˈ䲿ᵪᣭਆ 1000 Ӫ䘋㹼䈳ḕˈ㔃᷌ྲл˖ ⭧ ྣ ઼ ↓ᑨ 442 514 956 ᆖ⭏ 1 2 3 4 5 6 7 8 9 10 ᒤࡍᡀ㔙 64 43 84 72 52 93 77 58 69 91 ᒤᓅᡀ㔙 72 50 86 80 50 90 78 57 72 95

色盲 38 6 44 和 480 520 1000 (1)试据此判断,色盲是否与性别有关?(a=0.01) (2)你认为是男性还是女性更容易患色盲?请说明理由
㢢ⴢ 38 6 44 ઼ 480 520 1000 ˄1˅ 䈅ᦞ↔ࡔˈᯝ㢢ⴢᱟоᙗ࡛ᴹޣ)˛ߙ = 0.01) ˄2˅ 䇔Ѫᱟ⭧ᙗ䘈ᱟྣᙗᴤᇩ᱃ᛓ㢢ⴢ˛䈧䈤᰾⨶⭡DŽ

中国科学技术大学 2005一2006学年第一学期考试试卷 考试科目:概率论与数理统计 得分: 学生所在系: 姓名 学号: (考期:2006年1月22日,闭卷,可用计算器) 一、设昆虫产卵个数服从参数为入的Ps1on分布,而每个卵孵化成幼虫的概率为P,且 各卵是否成虫彼此之间没有关系。试求: (1)一个昆虫产生k个后代的概率: (2)若某个昆虫产生k个后代,求它产生m个卵的概率 二、设二维随机变量(X,Y)的联合密度为: fx,)=0.251+xylx<1,b1<1 0,others (1)求给定X=12时Y的条件概率密度: (2) 求Cov(X,Y)和Var(YJX=12): (3) 证明x2与Y2独立 三、设某学校有5000名学生,在某一时间区间内每个学生去某个阅览室的概率为0.05, 且设每个学生是否去该阅览室是相互独立的。试问该阅览室至少需要设多少座位才 能以95%的概率保证每个到该阅览室来的同学均有座位? 四、设从总体 X012 3 P82838/21-30 抽取的一个简单随机样本X1.,X1o的观测值为0,3,1,1,0,2,0.0,3,0) ()求9的矩估计量,和极大似然估计量商: (2)证明上述估计量都是无偏估计量 (3)比较这两个估计量,指出哪个更有效 五、假设某台精盐包装机生产的袋装盐的净重服从正态分布,按照要求每袋盐的标准重 量为500g,标准差不得超过10g。某天开工后,从装好的盐中随机抽取10袋,测得 其净重(单位:g)为:510,495,478,487,501,493,528,504,503,504。 试据此判断这时机器的工作是否正常。(a=0.05) 六、在著名的豌豆实验中,孟德尔(1822-1884)同时考虑豌豆的颜色和形状,共有四 种组合:(黄、圆),(黄、皱),(绿、圆),(绿、皱)。按孟德尔的理论,这四类应 该有9:3:3:1的比例。在一次实验中,发现这四类的观察数分别为315,101, 108和32试据此制断孟德尔的理论品否正确?(三005)
ѣള〇ᆜᢶᵥཝᆜ 2005—2006 ᆜᒪㅢжᆜᵕ㘹䈋䈋ভ 㘳䈅、ⴞ˖ᾲ⦷䇪оᮠ⨶㔏䇑 ᗇ ࠶ ˖ ᆖ⭏ᡰ൘㌫˖ ဃ ᆖ ਧ˖ ˄㘳ᵏ˖2006 ᒤ 1 ᴸ 22 ᰕˈ䰝ধˈਟ⭘䇑㇇ಘ˅ аǃ䇮ᰶ㲛ӗথњᮠᴽӾ৲ᮠѪɉⲴ Possion ࠶ᐳˈ㘼⇿њথᆥॆᡀᒬ㲛Ⲵᾲ⦷Ѫ pˈф থᱟᡀ㲛ᖬ↔ѻ䰤⋑ᴹޣ㌫DŽ䈅≲˖ ˄1˅ањᰶ㲛ӗ⭏ k њਾԓⲴᾲ⦷˗ ˄2˅㤕Ḁњᰶ㲛ӗ⭏ k њਾԓˈ≲ᆳӗ⭏ m њথⲴᾲ⦷DŽ Ҽǃ䇮Ҽ㔤䲿ᵪਈ䟿(X,Y)Ⲵ㚄ਸᇶᓖѪ˖ ൜ = (ݕ ,ݔ)f 0.25(1 + ݕݔ|,(ݔ > |1, |ݕ > |1 ݏݎ݄݁ݐ , 0 ˄1˅ ≲㔉ᇊ X=1/2 ᰦ Y ⲴᶑԦᾲ⦷ᇶᓖ˗ ˄2˅ ≲ Cov(X,Y)઼ Var(Y|X=1/2)˗ ˄3˅ 䇱᰾ܺଶоܻଶ⤜・DŽ йǃ䇮Ḁᆖṑᴹ 5000 ᆖ⭏ˈ൘Ḁаᰦ䰤४䰤⇿њᆖ⭏৫Ḁњ䰵㿸ᇔⲴᾲ⦷Ѫ 0.05ˈ ф䇮⇿њᆖ⭏ᱟ৫䈕䰵㿸ᇔᱟӂ⤜・ⲴDŽ䈅䰞䈕䰵㿸ᇔ㠣ቁ䴰㾱䇮ཊቁᓗս 㜭ԕ 95%Ⲵᾲ⦷؍䇱⇿њࡠ䈕䰵㿸ᇔᶕⲴ਼ᆖ൷ᴹᓗս˛ ഋǃ䇮Ӿᙫփ X 0 1 2 3 P Ʌ/2 Ʌ 3Ʌ/2 1-3Ʌ ᣭਆⲴањㆰঅ䲿ᵪṧᵜܺଵ, ڮܺ , ଵⲴ㿲⍻٬Ѫ(0,3,1,1,0,2,0,0,3,0)DŽ ˄1˅≲ ɅⲴ⸙ՠ䇑䟿ߠ ெ઼ᶱབྷլ❦ՠ䇑䟿ߠ ˗ ˄2˅䇱᰾к䘠ՠ䇑䟿䜭ᱟᰐٿՠ䇑䟿˗ ˄3˅∄䖳䘉єњՠ䇑䟿ˈᤷࠪଚњᴤᴹ᭸DŽ ӄǃۇٴ䇮Ḁਠ㋮ⴀव㻵ᵪ⭏ӗⲴ㺻㻵ⴀⲴ߰䟽ᴽӾ↓ᘱ࠶ᐳˈ᤹➗㾱≲⇿㺻ⴀⲴḷ߶䟽 䟿Ѫ 500gˈḷ߶ᐞнᗇ䎵䗷 10gDŽḀཙᔰᐕਾˈӾ㻵ྭⲴⴀѝ䲿ᵪᣭਆ 10 㺻ˈ⍻ᗇ ަ߰䟽˄অս˖g˅Ѫ˖510ˈ495ˈ478ˈ487ˈ501ˈ493ˈ528ˈ504ˈ503ˈ504DŽ 䈅ᦞ↔ࡔᯝ䘉ᰦᵪಘⲴᐕᱟ↓ᑨDŽ˄ߙ = 0.05˅ ޝǃ൘㪇Ⲵ䉼䉶ᇎ傼ѝˈᆏᗧቄ˄1822-1884˅਼ᰦ㘳㲁䉼䉶Ⲵ仌㢢઼ᖒ⣦ˈޡᴹഋ ⿽㓴ਸ˖˄哴ǃശ˅ˈ˄哴ǃⳡ˅ˈ˄㔯ǃശ˅ˈ˄㔯ǃⳡ˅DŽ᤹ᆏᗧቄⲴ⨶䇪ˈ䘉ഋ㊫ᓄ 䈕ᴹ 9˖3˖3˖1 Ⲵ∄ֻDŽ൘а⅑ᇎ傼ѝˈਁ⧠䘉ഋ㊫Ⲵ㿲ሏᮠ࡛࠶Ѫ 315ˈ101ˈ 108 ઼ 32.䈅ᦞ↔ࡔᯝᆏᗧቄⲴ⨶䇪ᱟ↓⺞˛˄ߙ = 0.05˅

中国科学技术大学 2005一2006学年第二学期考试试卷 考试科目:概率论与数理统计 得分: 学生所在系: 姓名 学号: (考期:2006年7月3日,闭卷,可用计算器 一、在空战中甲机先向乙机开火,击落乙机的概率为0.2:若乙机未被击落,就进行还 击,击落甲机的概率为0.3:若甲机未被击落,则再进攻乙机,击落乙机的概率为 04试求在这二回合中 (1)乙机被击落的概率是多少? (2)若乙机被击落,则它在第一回合中被击落的概率是多少? 二、设X~(o85)X2(085),且PxX2=0)=1。试求: (1)试求(X1,X2)的分布 (2)X1与X2是否独立?为什么? (3)X1与X2是否不相关?为什么? 三、设X与Y相互独立,都服从指数分布,参数分别为与≠,试求Z的概率密 度2(),其中:(1)Z=X+Y:(2)Z=X-Y. 四、设样本X,Xn抽自总体X,X服从(日,9+1)上的均匀分布: (1)试求8的矩估计©和极大似然估计8: (2)证明a1=又-与02=X)-均为0的无偏估计: (3)可1和82哪个更有效? 五、设样本X1.,Xn抽自正态总体N(以,σ2),问在下列三个统计量中: 5=(-)2,5经=二(X-)2,S学=(-X2 谁是σ2的无偏估计?谁对σ2的均方误差E(S经-σ2)最小?请证明你的结论。 六、某校组织学生参加英文词汇训练,并在年初与年底(即训练前与训后)各举行一次 阅读考试,以考察训练的效果。现随机抽取10名同学,将其年初与年底的考试成 绩记录如下 (1)假定两次考分之差服从正态分布,试由此判断词汇训练是否有显著效果?(在 a=0.05的水平下检验) (2)若上述两组数据并非抽自相同的10名同学,而是分别从两次考分中各随机抽取10
ѣള〇ᆜᢶᵥཝᆜ 2005—2006 ᆜᒪㅢӂᆜᵕ㘹䈋䈋ভ 㘳䈅、ⴞ˖ᾲ⦷䇪оᮠ⨶㔏䇑 ᗇ ࠶ ˖ ᆖ⭏ᡰ൘㌫˖ ဃ ᆖ ਧ˖ ˄㘳ᵏ˖2006 ᒤ 7 ᴸ 3 ᰕˈ䰝ধˈਟ⭘䇑㇇ಘ˅ аǃ൘オᡈѝ⭢ᵪݸ҉ੁᵪᔰ⚛ˈࠫ㩭҉ᵪⲴᾲ⦷Ѫ 0.2˗㤕҉ᵪᵚ㻛ࠫ㩭ˈቡ䘋㹼䘈 ࠫˈࠫ㩭⭢ᵪⲴᾲ⦷Ѫ 0.3˗㤕⭢ᵪᵚ㻛ࠫ㩭ˈࡉ䘋᭫҉ᵪˈࠫ㩭҉ᵪⲴᾲ⦷Ѫ 0.4.䈅≲൘䘉йഎਸѝ˖ ˄1˅҉ᵪ㻛ࠫ㩭Ⲵᾲ⦷ᱟཊቁ˛ ˄2˅㤕҉ᵪ㻛ࠫ㩭ˈࡉᆳ൘ㅜаഎਸѝ㻛ࠫ㩭Ⲵᾲ⦷ᱟཊቁ˛ Ҽǃ䇮ܺଵ~ ቀ ିଵ, , ଵ .ଶହ, .ହ, .ଶହቁˈܺଶ~ ቀ , ଵ .ହ, .ହቁ ˈфP{ܺଵܺଶ = 0} = 1DŽ䈅≲˖ ˄1˅䈅≲(ܺଵ,ܺଶ)Ⲵ࠶ᐳ˗ ˄2˅ܺଵоܺଶᱟ⤜・˛ѪӰѸ˛ ˄3˅ܺଵоܺଶᱟнޣ˛ѪӰѸ˛ йǃ䇮 X о Y ӂ⤜・ˈ䜭ᴽӾᤷᮠ࠶ᐳˈ৲ᮠ࡛࠶Ѫߣоߤ)ߣ ് ߤˈ(䈅≲ Z Ⲵᾲ⦷ᇶ ᓖ݂(ݖަˈ(ѝ˖˄1˅Z=X+Y˗˄2˅Z=X-YDŽ ഋǃ䇮ṧᵜܺଵ, ڮܺ , ᣭ㠚ᙫփ XˈX ᴽӾ(ߠ ,ߠ + 1)кⲴ൷र࠶ᐳ˖ ˄1˅䈅≲ߠⲴ⸙ՠ䇑ߠ઼ᶱབྷլ❦ՠ䇑כߠ˗ ˄2˅䇱᰾ߠ ଵ = ܺത െ ଵ ଶ ߠо ଶ = ܺ() െ ାଵ ൷ѪߠⲴᰐٿՠ䇑˗ ߠ˅3 ˄ ߠ઼ଵ ଶଚњᴤᴹ᭸˛ ӄǃ䇮ṧᵜܺଵ, ڮܺ , ᣭ㠚↓ᘱᙫփܰ(ߤ ,ߪଶ)ˈ䰞൘лࡇйњ㔏䇑䟿ѝ˖ ܵଵ ଶ = ଵ ିଵ σ (ܺ െ ܺത) ଶ ଵ ˈܵଶ ଶ = ଵ σ (ܺ െ ܺത) ଶ ଵ ˈܵଷ ଶ = ଵ ାଵ σ (ܺ െ ܺത) ଶ ଵ 䈱ᱟߪଶⲴᰐٿՠ䇑˛䈱ሩߪଶⲴ൷ᯩ䈟ᐞܧ൫ܵ ଶ െ ߪଶ൯ ଶ ᴰሿ˛䈧䇱᰾Ⲵ㔃䇪DŽ ޝǃḀṑ㓴㓷ᆖ⭏৲࣐㤡᮷䇽≷䇝㓳ˈᒦ൘ᒤࡍоᒤᓅ˄ণ䇝㓳ࡽо䇝ਾ˅Ѯ㹼а⅑ 䰵䈫㘳䈅ˈԕ㘳ሏ䇝㓳Ⲵ᭸᷌DŽ⧠䲿ᵪᣭਆ 10 ਼ᆖˈሶަᒤࡍоᒤᓅⲴ㘳䈅ᡀ 㔙䇠ᖅྲл˖ ˄1˅ۇٴᇊє⅑㘳࠶ѻᐞᴽӾ↓ᘱ࠶ᐳˈ䈅⭡↔ࡔᯝ䇽≷䇝㓳ᱟᴹᱮ㪇᭸᷌˛˄൘ ߙ = 0.05Ⲵ≤ᒣлỰ傼˅ ˄2˅㤕к䘠є㓴ᮠᦞᒦ䶎ᣭ㠚਼Ⲵ 10 ਼ᆖˈ㘼ᱟ࡛࠶Ӿє⅑㘳࠶ѝ䲿ᵪᣭਆ 10

人,并假定两次考分分别服从正态分布(二总体独立),方差未知但相等,试据以 判断词汇训练是否有显著效果?(在a=0.05的水平下检验) 学生 12345678910 年初成绩64438472529377586991 年底成绩72508680509078577295 参考答案 -、(1)0.2+0.8*0.7*0.4-0.424 (2)0.2/0.424=0.472 二、(1)略:(2)不独立:(3)不相关 三、(1)fz(2)=(e-e-),z20 ②a=e也,z20 (e,z<0 四、(1)6=8-6*e[Xm-1,Xal (2)略 (3)hd,广品Vhar(0,)=mn西n≤7,a有效:n之80有效 五、(1)S子=二(%:-)为无偏估计量:(2)均方误差排序S号<S经<S子 六、(1)成对数据检验,拒绝原假设:(2)两样本1检验,无法拒绝原假设
Ӫˈᒦۇٴᇊє⅑㘳࡛࠶࠶ᴽӾ↓ᘱ࠶ᐳ˄Ҽᙫփ⤜・˅ˈᯩᐞᵚ⸕նㅹˈ䈅ᦞԕ ࡔᯝ䇽≷䇝㓳ᱟᴹᱮ㪇᭸᷌˛˄൘ߙ = 0.05Ⲵ≤ᒣлỰ傼˅ ৲㘳ㆄṸ аǃ˄1˅0.2+0.8*0.7*0.4=0.424 ˄2˅0.2/0.424=0.472 Ҽǃ˄1˅⮕˗˄2˅н⤜・˗˄3˅нޣ йǃ˄1˅݂(ݖ = (ఒఓ ఒିஜ ൫݁ିఓ௭ െ ݁ିఒ௭൯, ݖ 0˗ (2) ݂(ݖ = (ቐ ఒఓ ఒାఓ ݁ିఒ௭, ݖ 0 ఒఓ ఒାఓ ݁ఓ௭, ݖ > 0 ഋǃ˄1˅ߠܺ = ത െ ଵ ଶ כߠ א ()ܺൣ െ 1,ܺ(ଵ)൧ ˄2˅⮕ ˄3˅Var(ߠ ଵ)= ଵ ଵଶ ߠVar൫ ଶ൯ = (ାଵ)మ(ାଶ) n 7, ߠ ଵᴹ᭸˗n 8, ߠ ଶᴹ᭸ ӄǃ˄1˅ܵଵ ଶ = ଵ ିଵ σ (ܺ െ ܺത) ଶ ଵ Ѫᰐٿՠ䇑䟿˗˄2˅൷ᯩ䈟ᐞᧂᒿܵଷ ଶ < ܵଶ ଶ < ܵଵ ଶ ޝǃ˄1˅ᡀሩᮠᦞỰ傼ˈᤂ㔍ۇٴ䇮˗˄2˅єṧᵜ t Ự傼ˈᰐ⌅ᤂ㔍ۇٴ䇮DŽ ᆖ⭏ 1 2 3 4 5 6 7 8 9 10 ᒤࡍᡀ㔙 64 43 84 72 52 93 77 58 69 91 ᒤᓅᡀ㔙 72 50 86 80 50 90 78 57 72 95