
偏振光的研究
偏振光的研究

前言 ÷干涉和衍射一光的波动性 ÷偏振一光是横波 。光的偏振现象 。偏振元件 。应用 学物理实验
大学物理实验 2 前言 ❖ 干涉和衍射—光的波动性 ❖ 偏振—光是横波 ❖ 光的偏振现象 ❖ 偏振元件 ❖ 应用

光的矢量性一光是横波 S=E×i K为波面的法线方向, S为光波的能量传播方 向。 S 在各向同性的介质中S 与K同向。在各向异性 的介质中S与K不同向。 0十一00一0十0十— 学物理实验
大学物理实验 3 S = E H K为波面的法线方向, S为光波的能量传播方 向。 在各向同性的介质中S 与K同向。在各向异性 的介质中S与K不同向。 E H S 光的矢量性 —光是横波
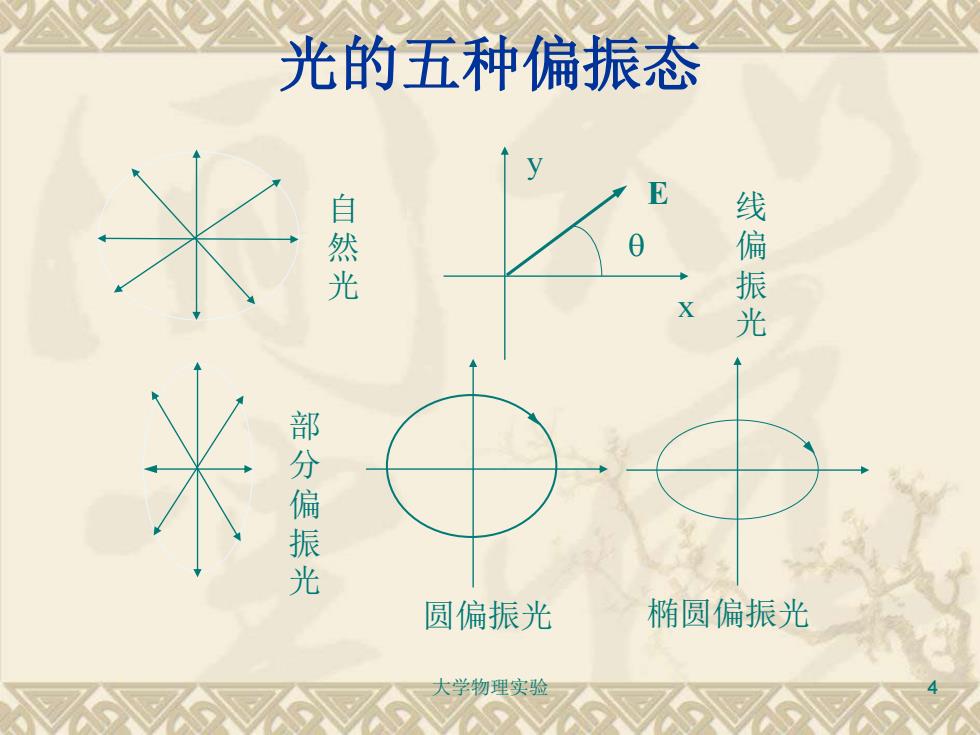
光的五种偏振态 冰 自然光 0 线偏振光 部分偏振光 圆偏振光 椭圆偏振光 学物理实骆
大学物理实验 4 E x y 自 然 光 部 分 偏 振 光 线 偏 振 光 圆偏振光 椭圆偏振光 光的五种偏振态

部分偏振度 定义: P= Imax-/min Imax+/min 学物理实验
大学物理实验 5 部分偏振度 ❖ 定义: max min max min I I I I P + − =

椭圆偏振光的形成(两个互相垂直的振动的合成) E Ex=Eox cos(@t+) E=Eoy cos(ot +a2) 椭圆方程式: E,2 ExE 十 2 Eo 2 2 EoxE vcosfan-a2)=sin2(a1-a2) (a1-02)=6=元/2正椭圆 Eox-Eoy-Eo }圆 大学物理实验
大学物理实验 6 椭圆偏振光的形成(两个互相垂直的振动的合成) ❖ 椭圆方程式: 2 cos( ) sin ( ) 1 2 2 1 2 0 0 2 0 2 2 0 2 + − − = − x y x y y y x x E E E E E E E E cos( ) cos( ) 0 2 0 1 = + = + E E t E E t y y x x (1 -2 )==/2 正椭圆 E0x= E0y= E0 } 圆 Ex Ey

改变光的偏振态的方法 1、利用偏振片 2、利用反射现象 3、利用双折射晶体 光的散射 学物理实验
大学物理实验 7 1、利用偏振片 2、利用反射现象 3、利用双折射晶体 光的散射 改变光的偏振态的方法

利用偏振片产生偏振光 非偏振光 线偏振光 + 十H→ 偏振片 学物理实验
大学物理实验 8 非偏振光 线偏振光 偏振片 利用偏振片产生偏振光
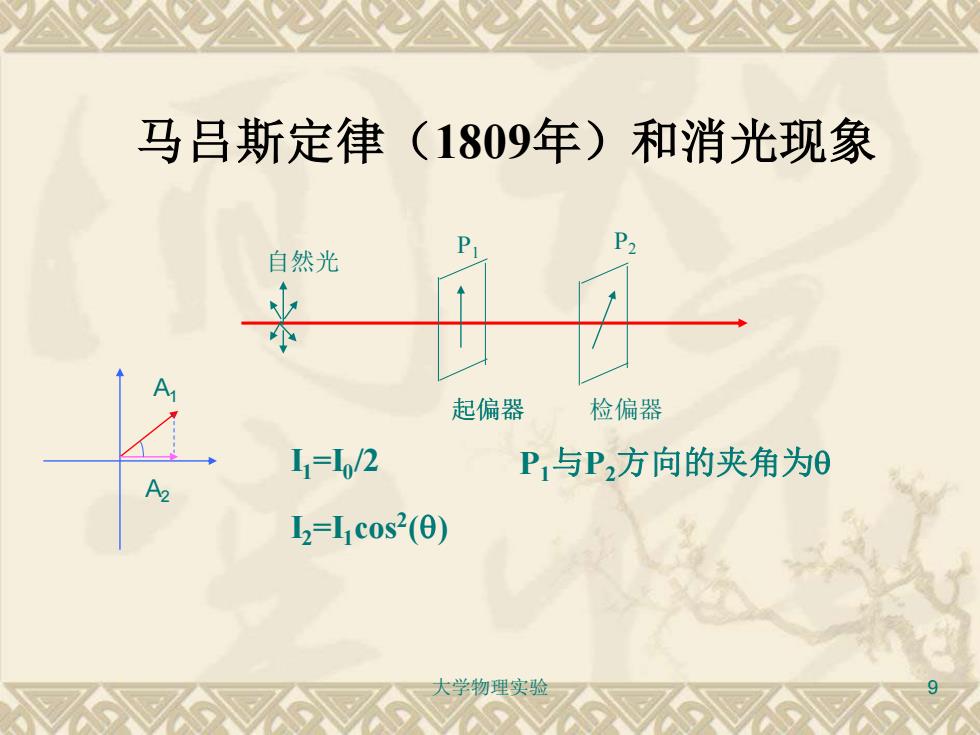
马吕斯定律(1809年)和消光现象 自然光 起偏器 检偏器 L1=/2 P与P2方向的夹角为0 L2=I1c0s2(0) 学物理实验
大学物理实验 9 马吕斯定律(1809年)和消光现象 自然光 P1 P2 起偏器 检偏器 I2=I1cos2 () I1=I0 /2 P1与P2方向的夹角为 A1 A2
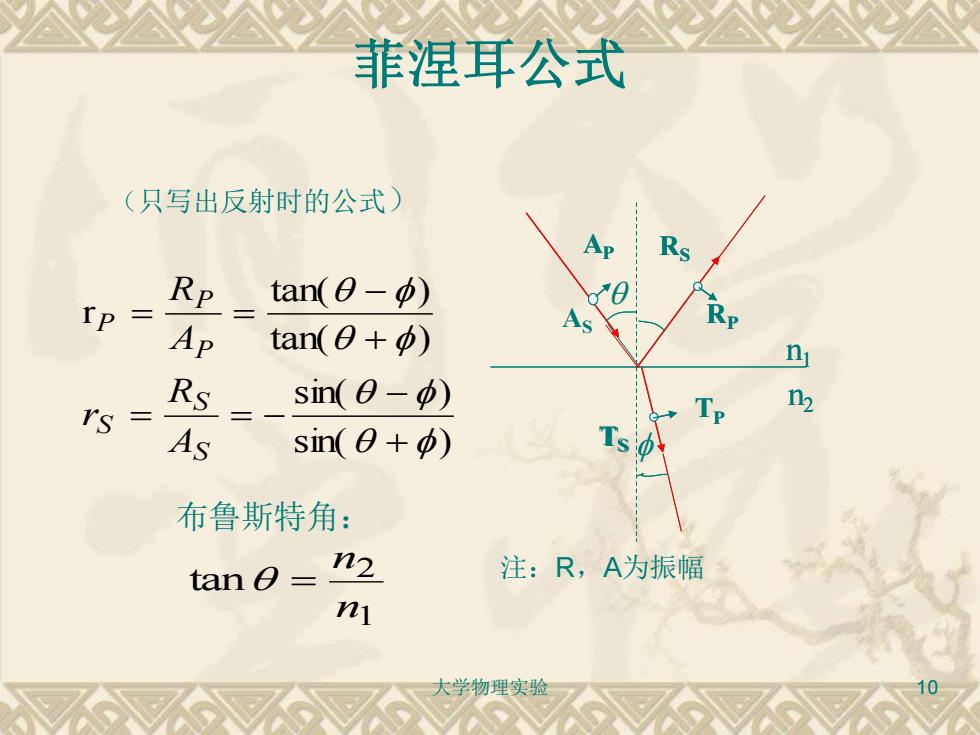
菲涅耳公式 (只写出反射时的公式) Rs tan(θ-p) Ip Ap tan(+) n in(θ-p) n, rs Rs=_ As sin(0+) Ts 布鲁斯特角: tan 9 n2 注:R,A为振幅 nj 学物理实验
大学物理实验 10 AP AS RP RS TP TS n1 n2 (只写出反射时的公式) sin( ) sin( ) tan( ) tan( ) r + − = = − + − = = S S S P P P A R r A R 布鲁斯特角: 注:R,A为振幅 菲涅耳公式 1 2 tan n n = AP RS RP TP TS n1 n2