
第二章静电场 2.1电场强度与电位函数 2.2静电场的基本方程 2.3电介质的极化 2.4静电场的边界条件 2.5导体系统的电容 2.6静电场的能量 2.7静电力
第二章 静 电 场 2.1 电场强度与电位函数 2.2 静电场的基本方程 2.3 电介质的极化 2.4 静电场的边界条件 2.5 导体系统的电容 2.6 静电场的能量 2.7 静电力

静止电荷产生的场表现为对于带电体有力的作用,这 种场称为电场。不随时间变化的电场称为静电场。 即空间位置及大小不随时间变化的电荷所产生的电场
静止电荷产生的场表现为对于带电体有力的作用,这 种场称为电场。不随时间变化的电场称为静电场。 即空间位置及大小不随时间变化的电荷所产生的电场

2.1电场强度与电位函数 2.1.1 库仑定律 电荷间的相互作用规律由库仑定律描述。真空 R=RR 中静止的电荷91对92的相互作用力,为 92 =19494R0=199R R 4π6R2 4π6R 91 电荷与电荷的相互作用 其中,应的单位为N(牛顿),g的单位为C〔库仑〕,成=方-产,方、分别为 点电荷和,的位置矢量,为矢量克的单位矢量。 1 = 4折×9x109 对8854×10也Fm,称为直空中的介电常薮。 BACK
2.1 电场强度与电位函数 2.1.1 库仑定律 电荷与电荷的相互作用 电荷间的相互作用规律由库仑定律描述。真空 中静止的电荷 q1 对 q2 的相互作用力 F12 为 R R q q R R q q F 3 1 2 0 0 2 1 2 0 12 4 1 4 1 = =

2.1.2电场强度 空间某点静电场的电场强度在数值上等于静电场对放置在该点的单位电 荷的作用力的大小,它的方向与正电荷在该点所受电场力的方向一致, 它表征了静电场对放置在该点的电荷的作用能力。若在电场强度 为E的空间某点放置点电荷q,则q受到的静电力为gE 库仑定律可导出空间点电荷q的电场强度为 E=,10=19R 4π8R2 4π8,R3 多个点电荷组成的电荷系统产生的电场 由矢量叠加原理,个点电荷组成的电荷系统在空间任意点激发 的电场为 4πeR 式中:R=产- BACK
空间某点静电场的电场强度在数值上等于静电场对放置在该点的单位电 荷的作用力的大小,它的方向与正电荷在该点所受电场力的方向一致, 它表征了静电场对放置在该点的电荷的作用能力。若在电场强度 为 E 的空间某点放置点电荷q ,则 q受到的静电力为 qE 库仑定律可导出空间点电荷q 的电场强度为 R R Q R R Q E 3 0 0 2 0 4 1 4 1 = = 多个点电荷组成的电荷系统产生的电场 由矢量叠加原理,N个点电荷组成的电荷系统在空间任意点激发 的电场为 3 0 1 1 4 N i i i i q E R = R = ' 式中: R r r i i = − 2.1.2 电场强度

源点:表明场源所在处的点, 用加撇的坐标表示 q(x',y,z) 如(x,y,z)或(r) R=立 9o(x,y,=) F=e,x'te y'te.z 场点:需要确定场量的点, 用不加撇的坐标表示 如(x,y,z)或(r) F=ex+ey+e.z 源点到场点之间的距离矢量可表示为 R=r-'=e(x-x')+e(y-y)+e.(2-) 点电荷q的电场强度为 E= 下-Fq(-) 4π6F-F2F-引4π6F-F
r' e x' e y' e z' = x + y + z 源点:表明场源所在处的点, 用加撇的坐标表示 如(x’,y ’ ,z ’ )或(r ‘) 场点:需要确定场量的点, 用不加撇的坐标表示 如(x,y,z)或(r) 源点到场点之间的距离矢量可表示为 点电荷q 的电场强度为 R r r' e (x x') e (y y') e (z z') = − = x − + y − + z − r e x e y e z = x + y + z 3 0 2 0 4 ' ( ) ' 4 ' r r q r r r r r r r r q E − − = − − − =

体电荷密度 体电荷:电荷连续分布在一定体积内形成的电荷体 体电荷密度p(的定义 在电荷空间V内,任取体积元AV,其中电荷量为△q 则 iAr-aqpdv p(r)=lim △g-dg 面电荷密度 面电荷:当电荷只存在于一个薄层上时,称电荷为面电荷 面电荷密度p,()的定义 在面电荷上,任取面积元△S,其中电荷量为△q h名器”>9-nh
体电荷:电荷连续分布在一定体积内形成的电荷体 体电荷密度 ( )r 的定义 0 ( ) limV q dq r V dV → = = 在电荷空间V内,任取体积元 V ,其中电荷量为 q 则 ( ) V q r dV = 体电荷密度 面电荷:当电荷只存在于一个薄层上时,称电荷为面电荷 面电荷密度 s ( )r 的定义 0 s ( ) limS q dq r S dS → = = 在面电荷上,任取面积元 S ,其中电荷量为 q 则 ( ) s S q r ds = 面电荷密度

线电荷度 线电荷:当电荷只分布在一条细线上时,称电荷为线电荷 线电荷密度P()的定义 在线电荷上,任取线元△1,其中电荷量为△9 则p)=m义-血>q=jP(ca 0△1dl 点电荷 当电荷体体积非常小,可忽略其体积时,称为点电荷。 点电荷可看作是电量q无限集中于一个几何点上。 p()=lim 90 r≠0 AW0△V∞ r=0
线电荷:当电荷只分布在一条细线上时,称电荷为线电荷 线电荷密度 l ( )r 的定义 0 l ( ) liml q dq r l dl → = = 在线电荷上,任取线元 l ,其中电荷量为 q 则 ( ) l l q r dl = 线电荷密度 0 0 0 ( ) limV 0 q r r V r → = = = 当电荷体体积非常小,可忽略其体积时,称为点电荷。 点电荷可看作是电量q无限集中于一个几何点上。 点电荷
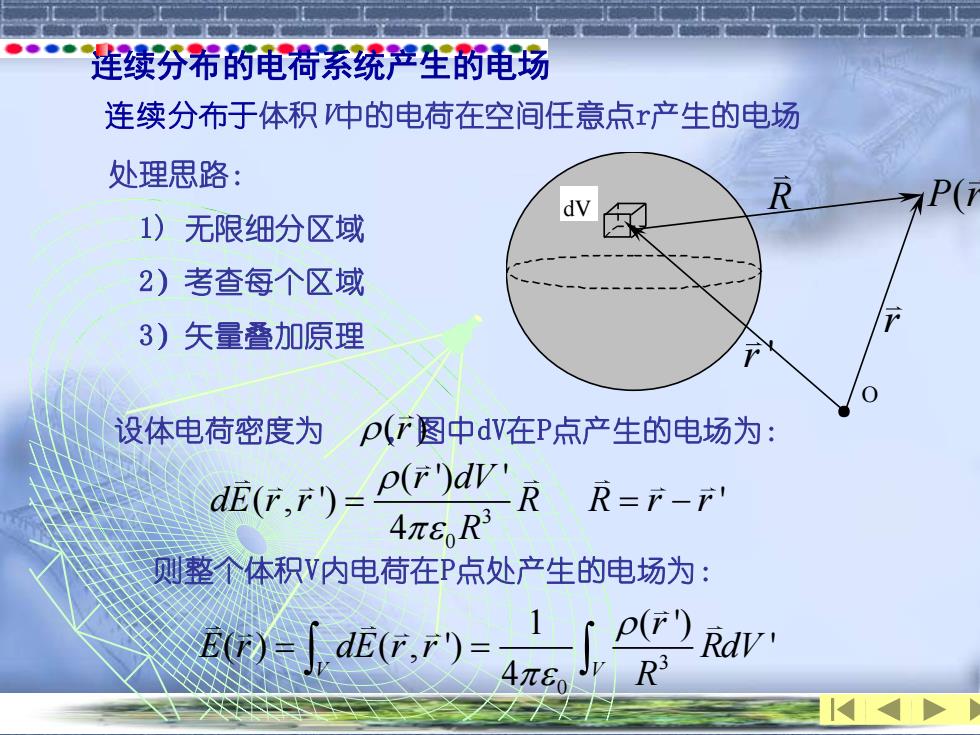
连续分布的电荷系统严生的电场 连续分布于体积仲的电荷在空间任意点产生的电场 处理思路: 1)无限细分区域 2)考查每个区域 3)矢量叠加原理 设体电荷密度为 p(r图中dV在P点产生的电场为: dE(F,F)= p(r)dv' R=r-r 4πER 则整个体积V内电荷在P点处产生的电场为:
连续分布的电荷系统产生的电场 连续分布于体积V中的电荷在空间任意点r产生的电场 O dV r ' r R P r( ) 处理思路: 1) 无限细分区域 2)考查每个区域 3)矢量叠加原理 3 0 ( ') ' ( , ') ' 4 r dV dE r r R R r r R = = − 设体电荷密度为 ( ) ,图中 r dV在P点产生的电场为: 则整个体积V内电荷在P点处产生的电场为: 3 0 1 ( ') ( ) ( , ') ' V V 4 r E r dE r r RdV R = =

面电荷和线电荷产生的电场只需在上式中将电荷体密度、体积元和积 分区域作相应替换即可,如 面电荷 4π5、 忘Jr 4元80 线电荷
面电荷和线电荷产生的电场只需在上式中将电荷体密度、体积元和积 分区域作相应替换即可,如 ( ) ( ) 0 1 ' 4 l l r R E r dl R = 3 线电荷 面电荷

对于体分布的电荷,r点的电场强度也可写为 E()= p()dv 4π8 F- 同理,面电荷和线电荷产生的电场强度分别为 E(F)=4 F一 π60 )ds r-F BACK
对于体分布的电荷, r点的电场强度也可写为 同理,面电荷和线电荷产生的电场强度分别为 ' ' 3 ' ' 0 ( ) 4 1 ( ) r ds r r r r E r s s − − = ' ' 3 ' ' 0 ( ) 4 1 ( ) r dl r r r r E r l l − − =