
《电磁场与电磁波》试题(8) 一、填空题(每小题1分,共10分) L.已知电荷体密度为P,其运动速度为下,则电流密度的表达式为: 2.设线性各向同性的均匀媒质中电位为,媒质的介电常数为5,电荷体密度为零,电位 所满足的方程为 3.时变电磁场中,平均坡印廷矢量的表达式为 4.时变电磁场中,变化的电场可以产生 5,位移电流的表达式为 6.两相距很近的等值异性的点电荷称为 7.恒定磁场是 场,故磁感应强度沿任一闭合曲面的积分等于零。 8.如果两个不等于零的矢量的叉积等于零,则此两个矢量必然相互 9.对平面电磁波而言,其电场、磁场和波的 三者符合右手螺旋关系。 10.由恒定电流产生的磁场称为恒定磁场,恒定磁场是连续的场,因此,它可用磁矢位函数 的 来表示 二、简述题(每小题5分,共20分) fn.d=fj00 ds 1.已知麦克斯韦第一方程为 ,试说明其物理意义,并写出方程 的微分形式。 12.什么是横电磁波? 13.从宏观的角度讲电荷是连续分布的。试讨论电荷的三种分布形式,并写出其数学表达式。 14.设任一失最场为A(),写出其穿过闭合曲线C的环量表达式,并讨论之。 三、计算题(每小题5分,共30分) 15.矢量1=8,2+6,3-4和B=6,求 (1)它们之间的夹角: (2)矢量A在B上的分量 16.矢量场在球坐标系中表示为E=色,r (1)写出直角坐标中的表达式: (2)在点1,2,2)处求出矢量场的大小. 17.某矢最场a=ey+,x,求 (1)矢量场的旋度:

(2)矢量场A的在点1,1)处的大小。 四、应用题(每小题10分,共30分) 18.自由空间中一点电荷电量为2C,位于S1,2,1)处,设观察点位于P3,4,5)处,求 (1)观察点处的电位: (2)观察点处的电场强度。 19.无限长同轴电缆内导体半径为a,外导体的内、外半径分别为b和℃。电缆中有恒定电 流流过 (内导体上电流为1、外导体上电流为反方向的1),设内、外导体间为空气,如图1 所示. (1)求ac处的磁场强度. 图1 20.平行板电容器极板长为a、笼为b,极板间距为d,如图2所示。设x=d的极板上的 自由电荷总最为,求 (1)电容器间电场强度: (2) 电容器极板间电压。 图2 五、综合题(10分) 21.平面电磁波在6,=960的媒质1中沿+z方向传插,在z=0处垂直入射到5,=460的 媒质2中,4=凸=山
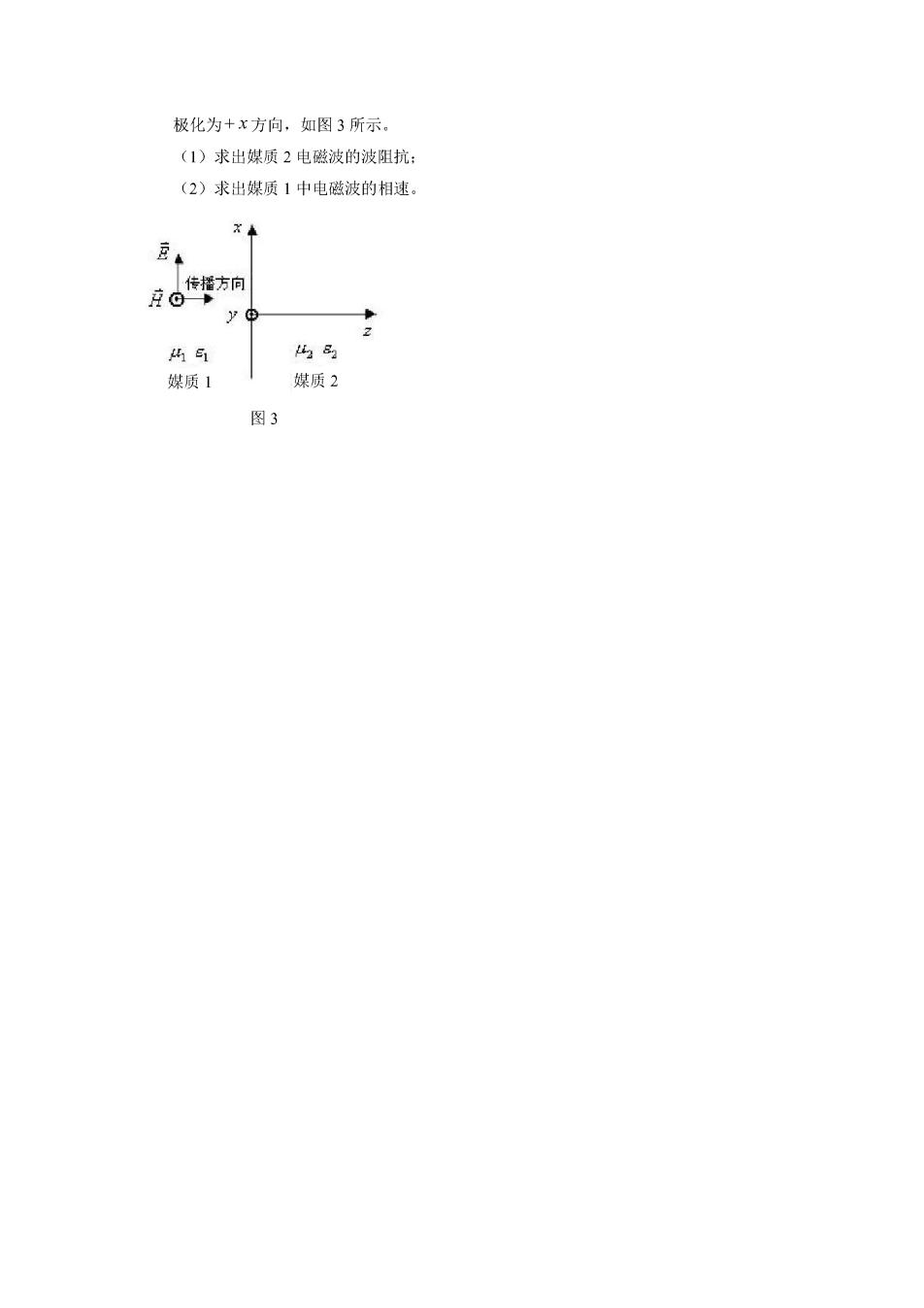
极化为+x方向,如图3所示, (1)求出媒质2电磁波的波阻抗: (2)求出媒质1中电磁波的相速。 9。为 码气 媒质1 媒质2 图3