
第九章波动光学 2024/130 制作:于国伟吉林大学 1
2024/1/30 制作:于国伟 吉林大学 1 第九章 波动光学

第一节 光的干涉现象 第二节 光的衍射现象 第三节 光的偏振现象
第三节 光的偏振现象 第二节 光的衍射现象 第一节 光的干涉现象

第一节光的干涉现象 一、预备知识 二、杨氏双缝干涉实验 三、薄膜干涉实验 四、劈尖干涉实验
第一节 光的干涉现象 四、劈尖干涉实验 三、薄膜干涉实验 二、杨氏双缝干涉实验 一、预备知识

一、预备知识 1、光的相千条件 (1)01≈02 且振动方向相同 (2)4≈4 (3)位相差固定且很小
1、光的相干条件 1 2 A1 A2 一、预备知识 (1) 且振动方向相同 (2) (3)位相差固定且很小

理想的光波 实际的光波(波列) 1、脉冲波。 2、波列@ 3、周期性波列
实际的光波(波列) 理想的光波

2、获得两束相干光源的方法 (1)分波面法:杨氏双缝干涉实验 (2)分振幅法:薄膜干涉实验 3、光程和光程差 (1)光在不同媒质中传播,相同时间内走过的路程不 同,但位相的改变相同。 如:在真空中的路程S=ct,在折射率为n的媒质中的 路程为L=v·t,L≤s,从相的角度来看L和S是 等效的,有:S=n·L (2)光程(optical path),折射率n与L的乘积称为光程。 引入光程的作用是:把光在媒质中的路程等效成真空中 的路程,光程常用δ表示,ò三n·L
2、获得两束相干光源的方法 3、光程和光程差 (1)光在不同媒质中传播,相同时间内走过的路程不 同,但位相的改变相同。 (2)分振幅法:薄膜干涉实验 (1)分波面法:杨氏双缝干涉实验 引入光程的作用是:把光在媒质中的路程等效成真空中 的路程,光程常用δ表示,δ=n·L 。 (2)光程(optical path),折射率n与L的乘积称为光程。 如:在真空中的路程S=ct,在折射率为n的媒质中的 路程为L=v·t, L<s ,从相的角度来看L和S是 等效的,有:S=n·L

(3)光程差:即两光程之差,通常也用6 表示光程差与相位差的关系。 2π6 重点 内容 △D= =1
重点 内容 (3)光程差:即两光程之差,通常也用δ 表示光程差与相位差的关系。 2 =

几点说明: ①光在真空中的光程就是其所走过的路程 'n=1,.δ=nL=L,路程是光程的一种特例。 ②光在不同折射率n、n2、. 的媒质中走过的路程若 为1、L2, 则总光程为: =nL+n2L2+ 11
①光在真空中的光程就是其所走过的路程 ∵n =1,∴δ= n·L= L ,路程是光程的一种特例。 ②光在不同折射率n1、n2、…… 的媒质中走过的路程若 为L1、L2、……,则总光程为: δ=n1L1+ n2L2+…… n L1 L2 a b 几点说明:

(4)合成后为极大的条件 重点 内容 光程差=波长整数倍 推导 c) e-oo) Y=Acos(ot+o)
( ) 1 0 1 1 1 1 1 cos = cos + + = − A t c r Y A t ( ) 2 0 2 2 2 2 2 cos = cos + + = − A t c r Y A t ( ) 0 Y = Acos t + 重点 内容 光程差=波长整数倍 推导 (4)合成后为极大的条件
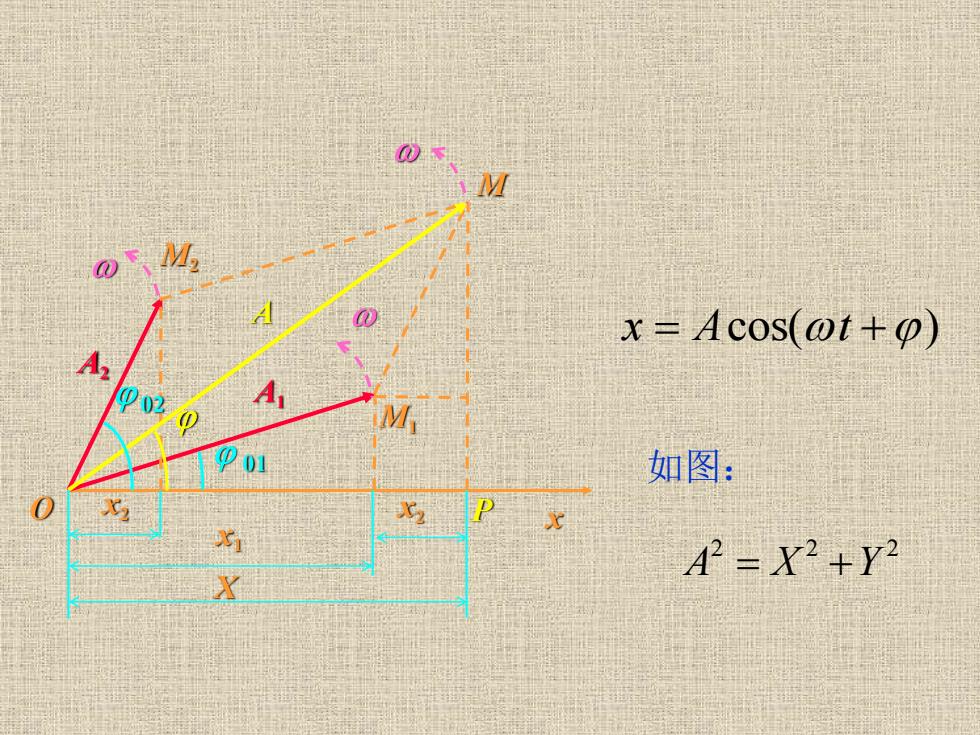
x=Acos(@t+) 02 如图: 2=X2+Y
2 2 2 A = X + Y 01 02 x2 x 2 x 1 x M2 M1 M AA 1 A 2 P X O 如图: x = Acos( t + )