
《电磁场与电磁波》试题(2)参考答案 二、简述题(每小题5分,共20分) 山.答:磁通连续性原理是指:磁感应强度沿任一闭合曲面的积分等于零,或者是从闭合 曲面S穿出去的通量等于由S外流入S内的通量。 (3分) 其数学表达式为:∮B·d5=0 (2分) 12.答:当一个矢量场的两类源(标量源和矢量源)在空间的分布确定时,该矢量场就唯一地 确定了,这一规律称为亥姆霍兹定理。 (3分) 亥姆霍兹定理告诉我们,研究任意一个矢量场(如电场、磁场等),需要从散度和旋度 两个方面去研究,或者是从矢量场的通量和环量两个方面去研究。(2分) 13.答:其物理意义:随时间变化的磁场可以产生电场。(3分) (2分) 14.答:电磁波的电场强度矢量的方向随时间变化所描绘的轨迹称为极化。(2分) 极化可以分为:线极化、圆极化、椭圆极化。(3分) 三、计算题(每小题10分,共30分) 15.矢量函数=-x2e,+z,试求 (1)V.A (2)V×A (3分 dx dy dz =-2.xy+y (2分 l ex V×A= (3分) (2) -1x 0 =ez+8x2 (2分) 16.矢量-2e,-2e,B-e,-e,求 (1)A-B

(2)求出两矢量的夹角 A-B=2e,-2e,-(e,-e,) (3分) 解:(1) -e,+e,-2e (2分) (2)根据A.B=AB cos0 (2分) B=(2e,-2e)e,-6,)=2 02i万月 2 (2分) 所以0=60 (1分) n.解.ww=袋+60+器 (3分) =e2x+e,2y+e2z (2分) a哥 (2分) 所以厅=2+e48,+e,2 (3分) √4+165 四、应用题(每小题10分,共30分) 18.放在坐标原点的点电荷在空间任一点F处产生的电场强度表达式为 (1)求出电力线方程:(2)画出电力线 条E=品品”品x++d (2分) 由力线方程得 x-y-2 ☆血正 (2分) 对上式积分得 y=Cx (1分) z=Cay 式中,C,C,为任意常数
(2)电力线图18-2所示 (注:电力线正确,但没有标方向得3分) ·(x,z) .g1,2,0) 图18-2 图1 19.设点电荷位于金属直角劈上方,如图1所示,求 (1)画出镜像电荷所在的位置 (2)直角劈内任意一点(化,八,z)处的电位表达式 解:(1)镜像电荷所在的位置如图191所示。 (注:画对一个镜像得2分,三个全对得5分) ·(x,,z) .q1.2.0) -20)-29 120),-.o) 图19-1 图19-2 (2)如图192所示任一点(化,八,z)处的电位为 品片制 (3分) 5=Vx-1+0-2+z 其中,5=y-+0+2分+2 (2分) =V(x+1+(y+2+ 4=Vx+1+0-2+z 20.设时变电磁场的电场强度和磁场强度分别为:

E=E。cos(i-p.) i=fi。cos(aom-pn)】 (1)写出电场强度和磁场强度的复数表达式 (2)证明其坡印延矢量的平均值为:S=E,×月,c08.-.) 解:(1)电场强度的复数表达式 E=E。e4 (3分) 电场强度的复数表达式 H=He-io (2分) (2)根据 5=RcE×F)得 (2分) 5n=)Rce。×AeM)=)E×月cos-) (3分) 五、综合题(共10分) 21.设沿+z方向传播的均匀平面电磁波垂直入射到理想导体,如图2所示,该电磁波电场 只有x分量即E-eEoe低 A ()求出反射波电场的表达式: (2)求出区域1媒质的波阻抗 黄为 , 理想导体 解:(1)设反射波电场 区域1 区域2 E,=e,E,eln 图2 区域1中的总电场为 E+E.=e,(Egei+Ee) (2分) 根据?=0导体表面电场的切向分量等于零的边界条件得 E.=-E。 (2分) 因此,反射波电场的表达式为 E,=-e Eoei 1分) (2)煤质1的波阻抗
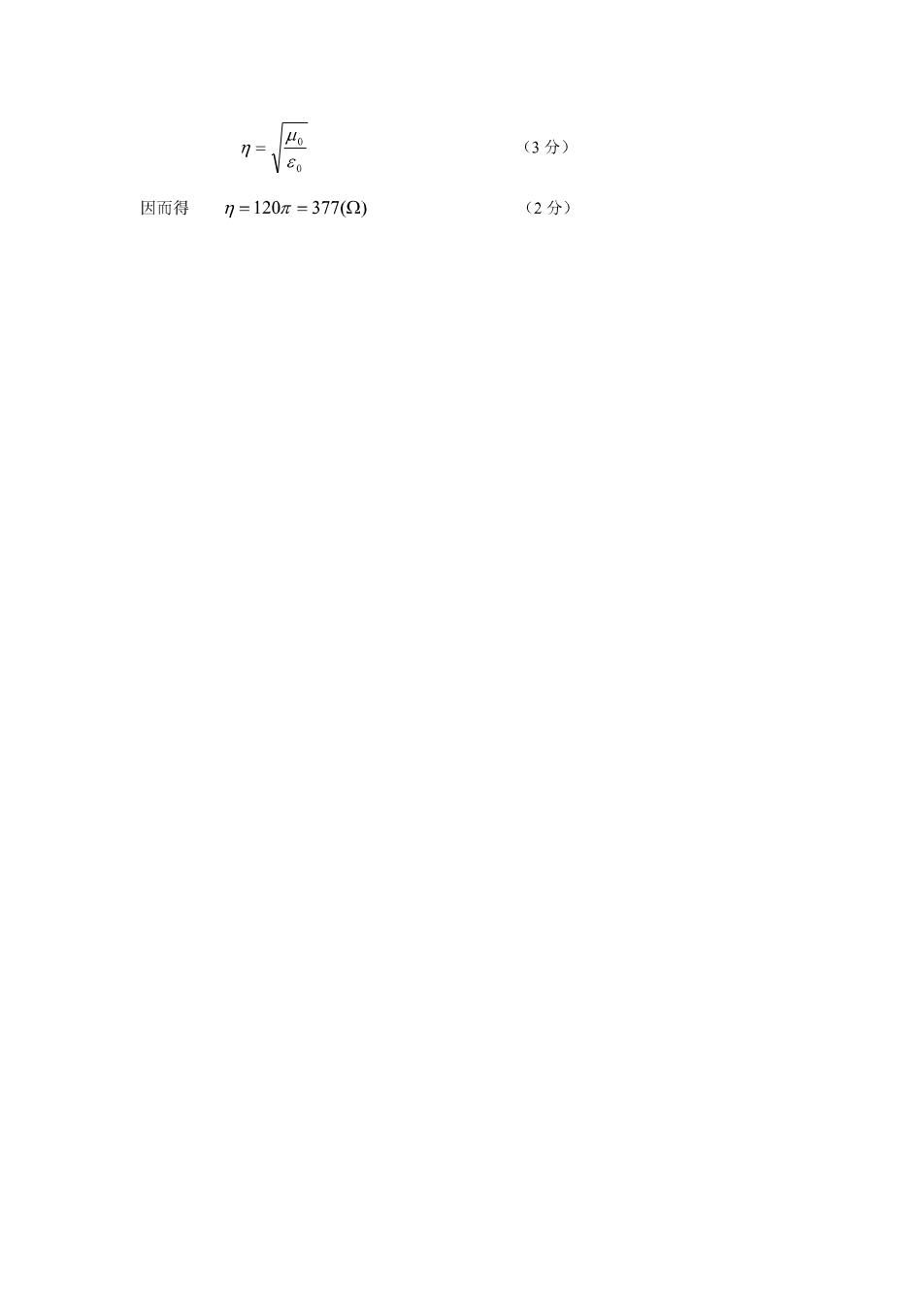
(3分) 因而得 7=120m=377(2) (2分)