
第一章振动和波动 振动(ibration):任何一个物理量在某一定 值附近随时间作反复变化。其中物体位置随时 间的变更称为机械振动。 波动(Wave):振动的传播 2024/130 制作:于国伟吉林大学 7
2024/1/30 制作:于国伟吉林大学 1 第一章 振动和波动 ▪振动(Vibration):任何一个物理量在某一 定 值附近随时间作反复变化。其中物体位置随时 间的变更称为机械振动。 ▪波动(Wave):振动的传播

内容提要 ■第一节简谐振动 ■第二节两个简谐振动的合成 ·第三节平面简谐波动 第四节两个平面简谐波动的合成 2024/1130 制作:于国伟吉林大学 2
2024/1/30 制作:于国伟吉林大学 2 内容提要 ◼ 第一节 简谐振动 ◼ 第二节 两个简谐振动的合成 ◼ 第三节 平面简谐波动 ◼ 第四节 两个平面简谐波动的合成

第一节简谐振动 简谐振动的基本特征 简谐振动的方程 简谐振动的矢量图解法 简谐振动的能量 2024/130 制作:于国伟吉林大学 3
2024/1/30 制作:于国伟吉林大学 3 第一节 简谐振动 • 简谐振动的基本特征 • 简谐振动的能量 • 简谐振动的方程 • 简谐振动的矢量图解法

简谐振动的基本特征 物体在一定 位置甜近作往 复的运动称为 认械振动 224 运动的形式: x=Acos(ot+o) 受力的形式:弹性力(回复力)F=-kx (注:是劲度系数或倔强系数)
一 简谐振动的基本特征 F = − k x cos( ) = +0 x A t (注:k是劲度系数或倔强系数) 2:24 受力的形式:弹性力(回复力) 运动的形式:

例一 直径d的U形管,装有质量为m的液体,若液 体一个小的初始位移,液体在管中作微振 动,这种振动是否是简谐振动 F=-△mg=-P△vg 2x 2ws小 图1-1 是简谐振动
例一 直径d的U形管,装有质量为m的液体,若液 体一个小的初始位移,液体在管中作微振 动,这种振动是否是简谐振动 . F = −mg = −v g 是简谐振动 d g x = −k x = − 2 2 1 g d x = − 2 2 2
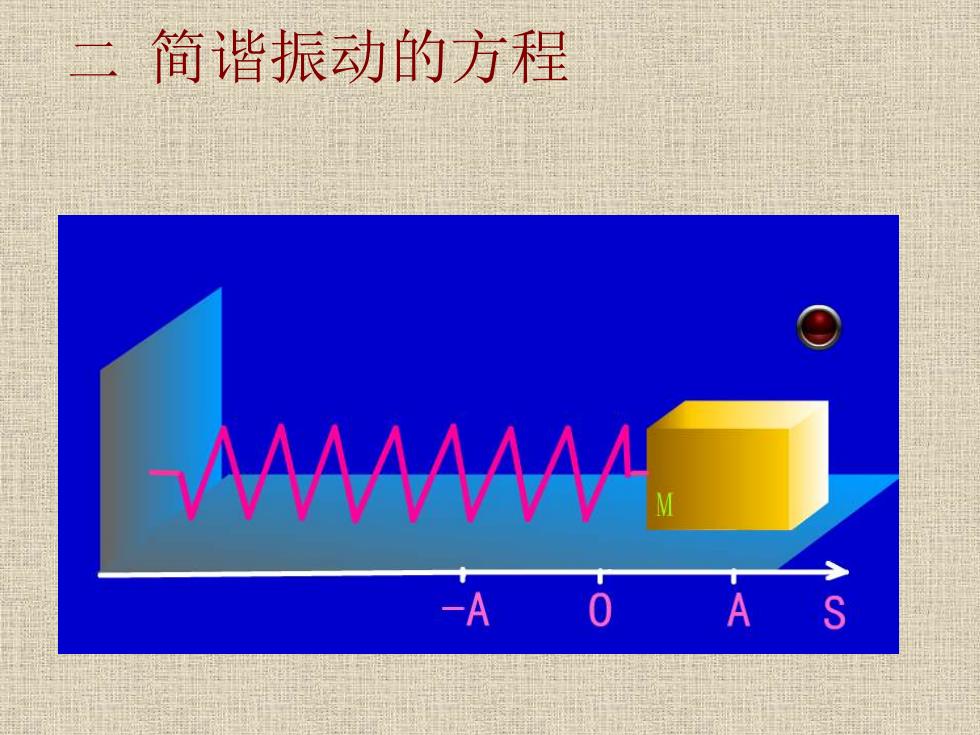
二简谐振动的方程 M4 -A 0 A S
二 简谐振动的方程
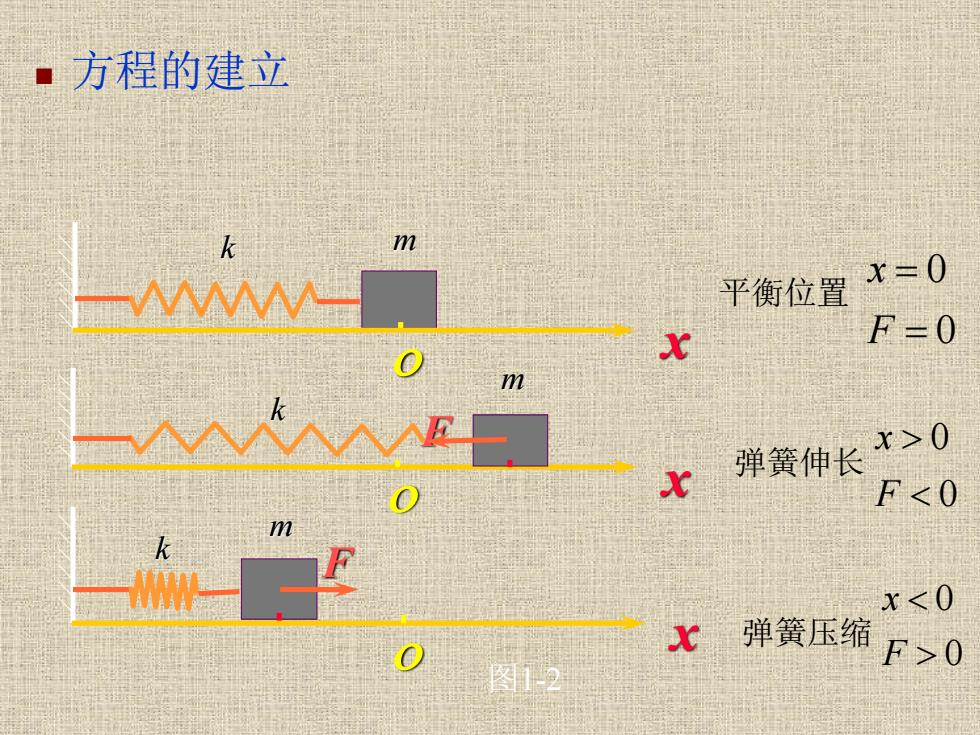
·方程的建立 m 平衡位置 x=0 x F=0 m X 弹簧伸长>0 F0 图12
◼ 方程的建立 o F x k m 0 0 F x 弹簧伸长 o x F k m 弹簧压缩 0 0 F x o x k m 平衡位置 0 0 = = F x 图1-2

·公式的推导 F=-kx F=ma= -kx人-0 dx→md d m dr 令 (o为微分常数) m 得到简谐振动的微分方程: d2¥+m2x=0 dt?
◼ 公式的推导 = = = − 2 2 dt d x F ma m F k x k x dt d x m = − 2 2 令 2 (为微分常数) m k = 0 2 2 2 + x = dt d x 0 2 2 + x = m k dt d x 得到简谐振动的微分方程:

其解为: 位移 x=Acos(ot+o) 利用速度和加速度的数学定义,可得: 速度 --wsmr+a) dt 加速度 a= d3=-o2 Acosf+0】 d (A与0为积分常数)
其解为: sin( ) = = − +0 A t dt dx v cos( ) 0 2 2 2 = = − A t + dt d x a cos( ) = +0 x A t ( ) A与0 为积分常数 加速度 速度 利用速度和加速度的数学定义,可得: 位移

简谐振动的位移、速度和加速度的函数曲线
简谐振动的位移、速度和加速度的函数曲线 x 0 t a V