
《电磁场与电磁波》试题2 一、填空题(每小题1分,共10分) 1.在均匀各向同性线性媒质中,设媒质的介电常数为8,则电位移矢量D和电场E满足的 方程为: 2.设线性各向同性的均匀媒质中电位为P,媒质的介电常数为£,电荷体密度为P,电位 所满足的方程为 3,时变电磁场中,坡印廷矢量的数学表达式为 4.在理想导体的表面,电场强度的 分量等于零, r)5 5.表达式 称为矢量场A(F)穿过闭合曲面S的 6.电磁波从一种媒质入射到理想导体表面时,电磁波将发生 7.静电场是保守场,故电场强度沿任一条闭合路径的积分等于 8.如果两个不等于零的矢量的点积等于零,则此两个矢量必然相互 9.对横电磁波而言,在波的传播方向上电场、磁场分量为 10.由恒定电流产生的磁场称为恒定磁场,恒定磁场是 场,因此,它可用磁矢 位函数的旋度来表示。 二、简述题(每小题5分,共20分) 山.试简述磁通连续性原理,并写出其数学表达式 12.简述亥姆霍兹定理,并说明其意义。 13.己知麦克斯韦第二方程为℃ ,试说明其物理意义,并写出方程的微 分形式。 14.什么是电磁波的极化?极化分为哪三种? 三、计算题(每小题10分,共30分) 15.矢量函数1=-r.+12e.n 1)V.a (2)V×a 16.矢量1=22,-2,B=e,-6,求 (1)4-B (2)求出两矢量的夹角

17.方程(xy)=x+y2+z给出一球族,求 (1)求该标量场的梯度: (2)求出通过点1,20)处的单位法向矢量 四、应用题(每小题10分,共30分) 18.放在坐标原点的点电荷在空间任一点F处产生的电场强度表达式为 (1)求出电力线方程:(2)画出电力线 19.设点电荷位于金属直角劈上方,如图1所示,求 (1)画出镜像电荷所在的位置 (2)直角劈内任意一点x,2)处的电位表达式 ·(xy2动 g1,2,0) 图1 20.设时变电磁场的电场强度和磁场强度分别为: E=E cos(o) H=H。cos(oM-pn) (1)写出电场强度和磁场强度的复数表达式 (2)证明其坡印廷矢量的平均值为: 5-,×月,co6.-6) 五、综合题(10分) 21,设沿+z方向传播的均匀平面电磁波垂直入射到理想导体,如图2所示,该电磁波电场 只有x分量即E=日E,e供 (①)求出反射波电场的表达式: (2)求出区域1媒质的波阻抗
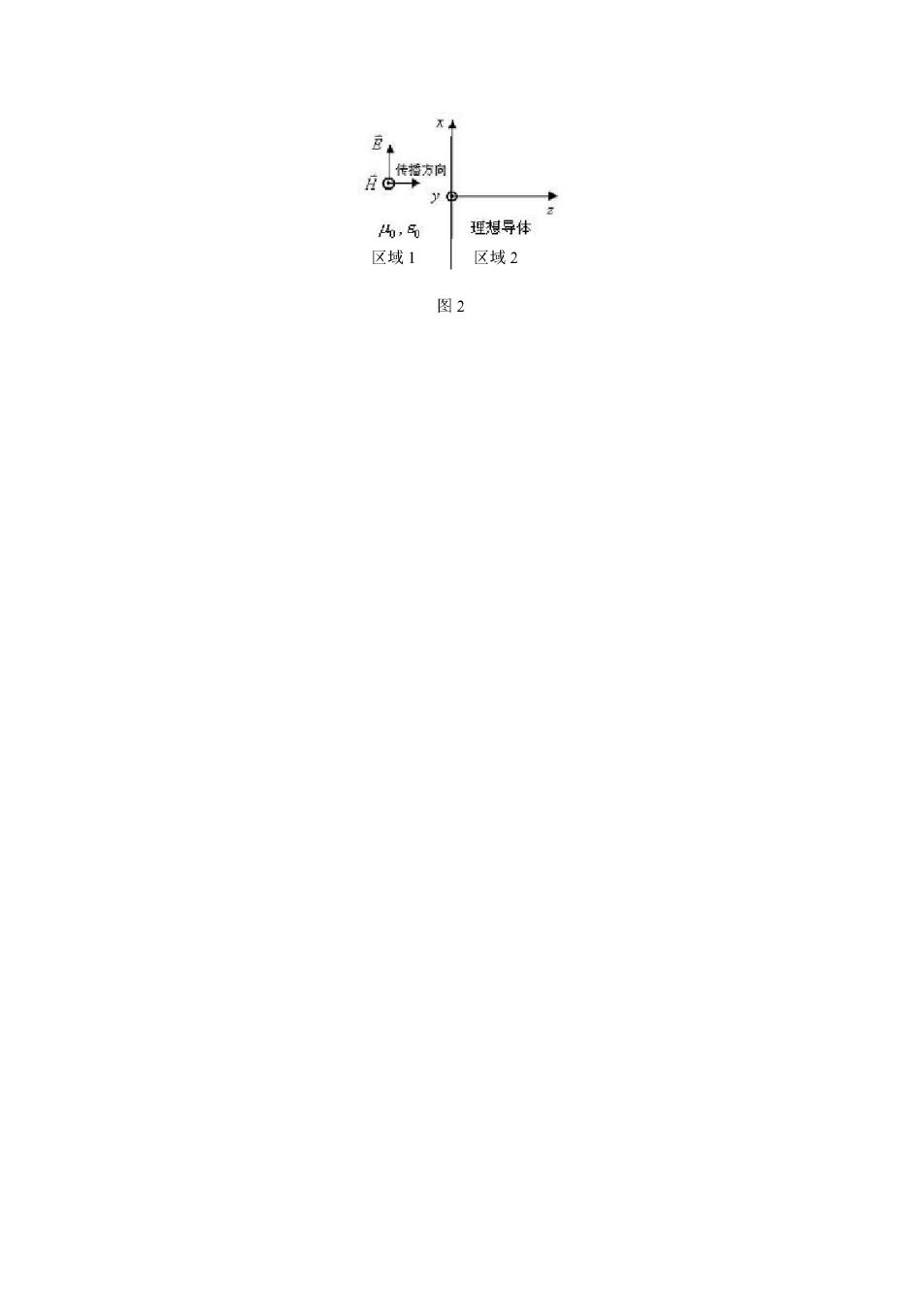
2。 理相导体 区域1 区域2 图2