
《电磁场与电磁波》试题(7)参考答案 二、简述题(每小题5分,共20分) 山.答:恒定电流所产生的不随时间变化的磁场称为恒定磁场: (3分) 它具有无散、有旋特性 (2分) V,B=0 V×月=j 12.答:当穿过线图所包围面积S的磁通发生变化时,线图回路C中将会感应一个电动势: (2分)感应电动势在闭合回路中引起的感应电流的方向是使它所产生的磁场阻止回路中磁 通的变化: (1分) Ed=-Bs (2分) 13.答:电磁波等相位面传播的速度称为相速。 (3分) 所谓群速则是包络或者是能量传播的速度: 相速v,与群速y的关系式为:y。= (2分) 、⊙w v。da 14.高斯通量定理的微分形式为7·D=P,试写出其积分形式,并说明其意义。 D.ds=[pydv=2 (3分) 它表明从封闭面发出的总电通量数值上等于包含在该封闭面内的净正电荷。(2分) 二、计算题(每小题10分,共30分) 15.自由空间中一点电荷位于S(-31,4),场点位于P2,-2,3) (1)写出点电荷和场点的位置矢量 (2)求点电荷到场点的距离矢量 解: (1) 点电荷位置矢量产=-3e.+e,+4 3分)

场点位置矢量 F=2e.-2e,+3e (2分) (2) 点电荷到场点的距离矢量 R=f,- (3分) 反=5e,-3e,-e (2分) 16。某二维标量函数4=y2-x,求 (1)标量函数梯度Vu (2)求梯度在正x方向的投影。 解: (1)对于二维标量场 + (3分) =-e,+2e (2分) (2)梯度在正x方向的投影 Vu.e,=-1 (5分) 17.矢量场A=ex+色,y+ez,求 (1)矢量场的散度 (2)矢量场A在点(山,2,2)处的大小 解: (1 vi=l+叫+4 (3分) dx dy 8z =1+1+1=3 (2分》 (2)矢量场A在点1,2,2)处的大小 |A=V2+y2+z (3分)
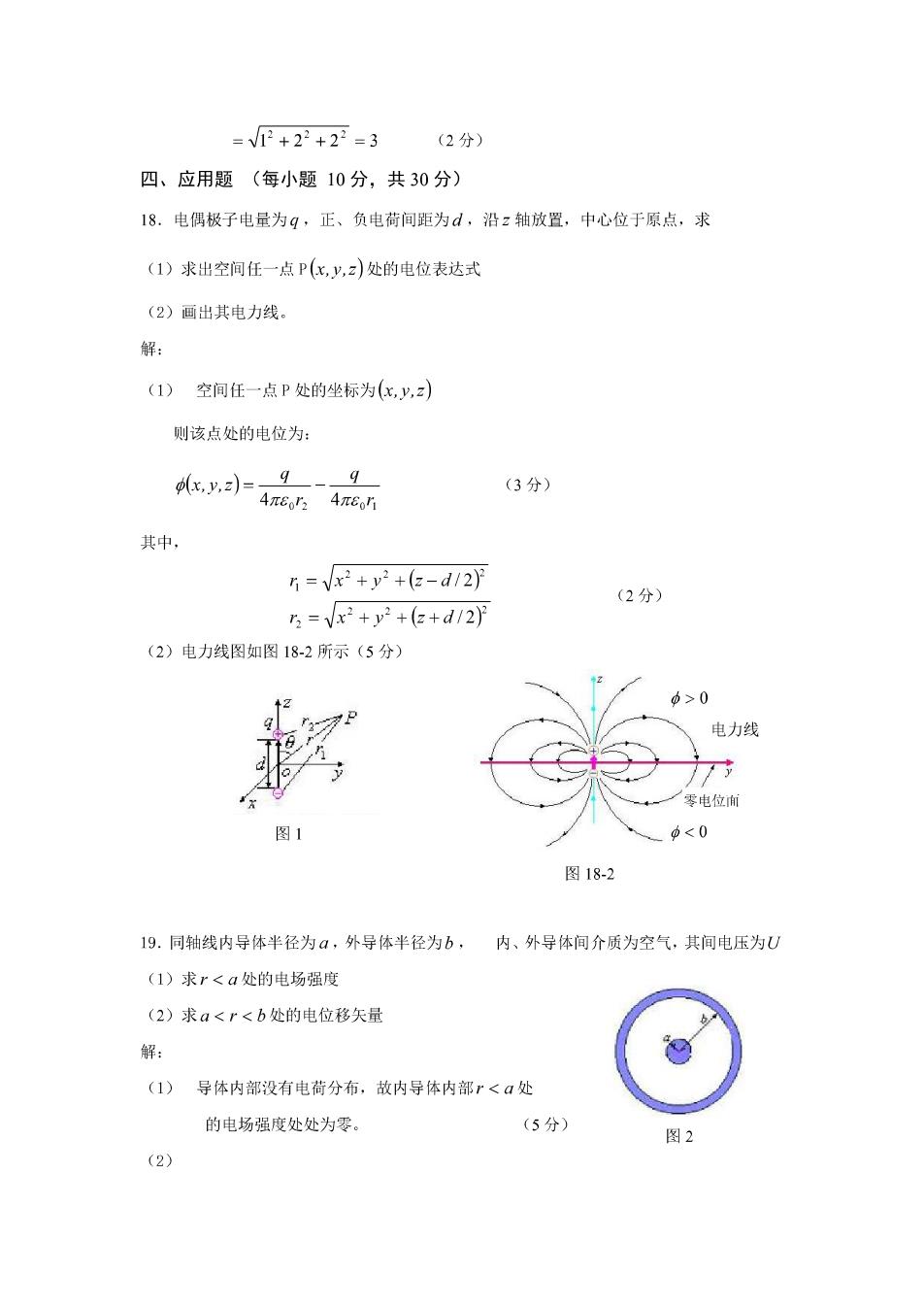
=2+22+22=3(2分) 四、应用题(每小题10分,共30分) 18.电偶极子电量为q,正、负电荷间距为d,沿z轴放置,中心位于原点,求 (1)求出空间任一点P(x,,)处的电位表达式 (2)画出其电力线。 解: (1)空间任一点P处的坐标为(x,y,z) 则该点处的电位为: x.y.4mco 9 (3分) 其中 1=VR2+y2+6-d/2奶 (2分) 3=Vx2+y2+(e+d12 (2)电力线图如图18-2所示(5分) >0 电力线 零电位间 图1 .<0 图18-2 19.同轴线内导体半径为a,外导体半径为b,内、外导体间介质为空气,其间电压为U (1)求r<a处的电场强度 (2)求a<r<b处的电位移矢 解: (1)导体内部没有电荷分布,故内导体内部r<a处 的电场强度处处为零。 (5分) 图2 (2)

设单位长内导体表面电荷密度为P,由电荷的分布对称性可知,离导线等距离处的电 场大小处处相等,方向为沿柱面径向,在底面半径为r长度为L的柱体表面使用高 斯定理得: fE5=∫E5+∫E+E,5 =2mLE,+0+0=p,L/60 可得a<r<b任一点处的电场强度为 E=6,26d P (3分) 再由 w--品品合 得a<r<b任一点处的电位移矢量为: D=6E=e.Hn(6/a) BU (2分) 20.已知钢在某种磁饱和情况下磁导率4=20004。,当钢中的磁感应强度 B=0.5×102T、日=75时,此时磁力线由钢进入自由空间一侧后,如图3所示。 求 B. (1)B,与法线的夹角0, 42=4 (2)磁感应强度B,的大小 4=20004 解: (1)由 图3 tana=凸 3分) tane,u tam8,=华an8 41 02=0.107 (2分)

(2)边界上电流为零,由边界条件 B,cos0 B:cose, (3分) 民=A B,=0.129×10-2T (2分) 五、综合题(10分) 21.平面电磁波在6,-9的媒质1中沿+z方向传播,在z=0处垂直入射到6,-46。的 媒质2中,4=4=4。极化为+x方向,如图4所示。 (1)求出媒质2中电磁波的相速: (2)透射系数。 解: y⊙ (1) 媒质2中电磁波的相速为: 媒质1 媒质2 1 :4.6246 分】 图4 -1.5x10ms 2分) 2) 唇要m (2分) 7-22 120m .+760x+40=12 (3分)