
第三章恒定电流的电场和难场 3.1恒定电流的电场 3.2磁感应强度 3.3恒定磁场的基本方程 3.4介质的磁化 3.5磁介质的场方程 3.6恒定磁场的边界条件 3.7矢量磁位和标量磁位 3.8 自感和互感 3.9 磁场能量与力
第三章 恒定电流的电场和磁场 3.1 恒定电流的电场 3.2 磁感应强度 3.3 恒定磁场的基本方程 3.4 介质的磁化 3.5 磁介质的场方程 3.6 恒定磁场的边界条件 3.7 矢量磁位和标量磁位 3.8 自感和互感 3.9 磁场能量与力

3.1恒定电流的电场 在空间中分布不随时间变化的电流称为恒定电流,与恒定 电流对应的电场称为恒定电场。 电流及电流强度 分类:传导电流与运流电流。 传导电流是导体中的自由电子(或空穴)或者是电解液中的离子 运动形成的电流。 运流电流是电子、离子或淇它带电粒子在真空或气体中运动形成 的电流
电流及电流强度 分类:传导电流与运流电流。 传导电流是导体中的自由电子(或空穴)或者是电解液中的离子 运动形成的电流。 运流电流是电子、离子或其它带电粒子在真空或气体中运动形成 的电流。 3.1 恒定电流的电场 在空间中分布不随时间变化的电流称为恒定电流,与恒定 电流对应的电场称为恒定电场

电流强度:单位时间内穿过某一截面的电量,又简称为电流, 以I表示。电流的单位为A(安培)。 因此,电流I与电荷g的关系为 I= dq dt 电流密度:是一个矢量,以J表示。电流密度的方向为正电荷 的运动方向,其大小为单位时间内垂直穿过单位面积的电荷量。 因此,穿过任一有向面元dS的电流d山与电流密度J的关系为 dI J.dS
电流强度:单位时间内穿过某一截面的电量,又简称为电流, 以 I 表示。电流的单位为A(安培)。 因此,电流 I 与电荷 q 的关系为 t q I d d = 电流密度:是一个矢量,以J 表示。电流密度的方向为正电荷 的运动方向,其大小为单位时间内垂直穿过单位面积的电荷量。 因此,穿过任一有向面元dS 的电流 dI 与电流密度 J 的关系为 J S dI = d
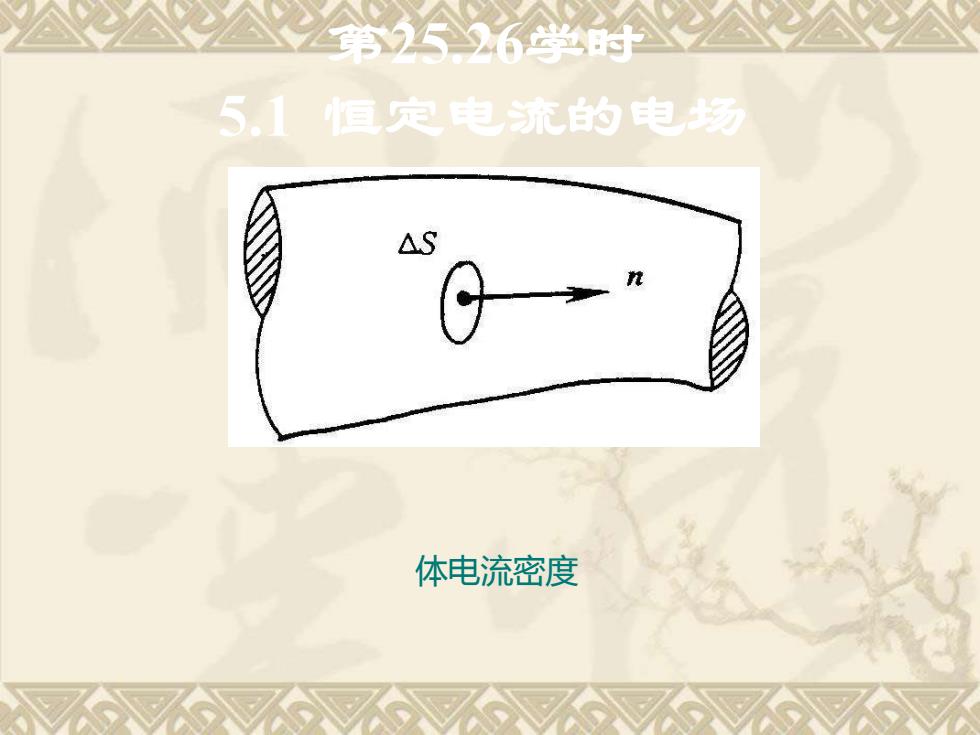
5.1恒定电流的电场 体电流密度
第25.26学时 5.1 恒定电流的电场 体电流密度

设通过AS的电流为△!, AI=PAS △t tv prAS 则该点处的电流密度J为 J=lim △Id =p As0△SdS 电流密度的单位是安培/米2(A/m)。导体内每一点都有一个电流密度, 因而构成一个矢量场。称这一矢量场为电流场。电流场的矢量线叫做 电流线。 可以从电流密度J求出流过任意面积S的电流强度。一般情况下,电流 密度J和面积元dS的方向并不相同。此时,通过面积S的电流就等于电 流密度在S上的通量,即 1=[J.dS-J cosads
设通过ΔS的电流为ΔI, 则该点处的电流密度 J为 电流密度的单位是安培/米2 (A/m2 )。导体内每一点都有一个电流密度, 因而构成一个矢量场。称这一矢量场为电流场。电流场的矢量线叫做 电流线。 可以从电流密度J求出流过任意面积S的电流强度。一般情况下,电流 密度J和面积元dS的方向并不相同。此时,通过面积S的电流就等于电 流密度J在S上的通量,即 = = S S I J dS J cosdS v S t S tv I = = v dS dI S I J S = = = →0 lim
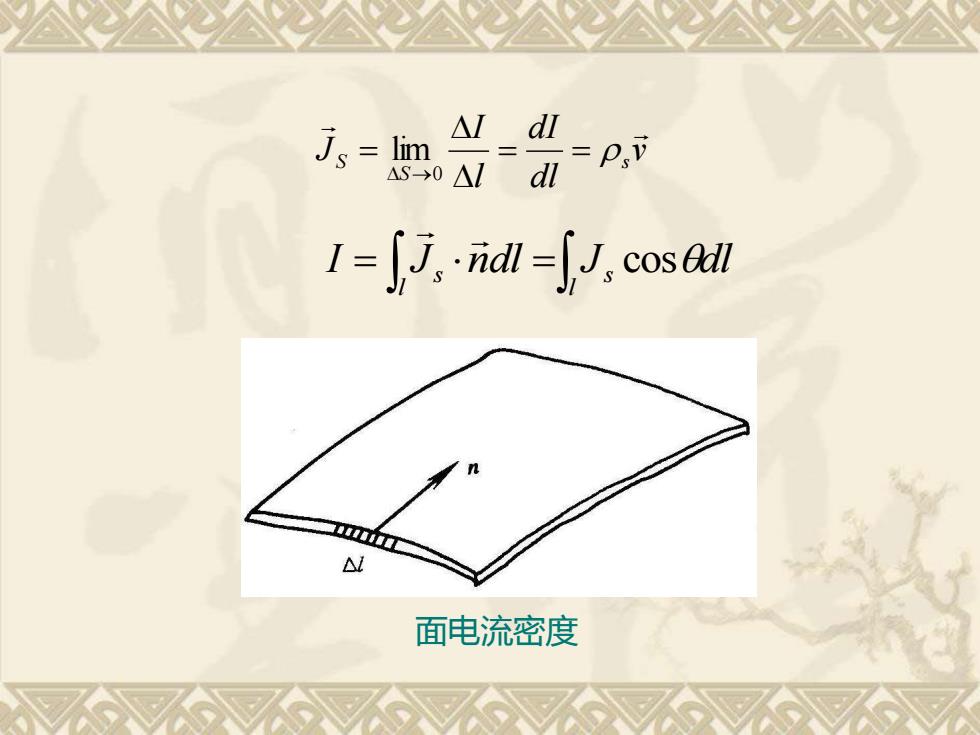
Js=lim △ld -0△1dl =P, l=jJ,-idl=∫J,cosl △ 面电流密度
面电流密度 v dl dI l I J s S S = = = →0 lim = = l s l I Js ndl J cosdl

运流电流的电流密度并不与电场强度成正比,而且电流密度的 方向与电场强度的方向也可能不同。可以证明运流电流的电流密度 J与运动速度v的关系为 J=pv 式中p为电荷密度。 与介质的极化特性一样,媒质的导电性能也表现出均匀与非均匀, 线性与非线性以及各向同性与各同异性等特点,这些特性的含义与 前相同。上述公式仅适用于各向同性的线性媒质
运流电流的电流密度并不与电场强度成正比,而且电流密度的 方向与电场强度的方向也可能不同。可以证明运流电流的电流密度 J 与运动速度 v 的关系为 J v = 式中 为电荷密度。 与介质的极化特性一样,媒质的导电性能也表现出均匀与非均匀, 线性与非线性以及各向同性与各同异性等特点,这些特性的含义与 前相同。上述公式仅适用于各向同性的线性媒质

÷1、欧姆定律的微分形式 实验表明在导电媒质中,当温度不变时,媒质中某点的电流密 度J与该点的电场强度E成正比 j=o尼 欧姆定律的微分形式 由于电流密度可以视为单位面积的电流密度,电场强度可以 视为在电场强度方向单位长度上的电压。 因此,对一段长为1, 横截面为$的导线,欧姆定律的微分 形式可写成: 1=4U R σ值愈大表明导电能力 愈强,即使在微弱的 △I=JaS 电场作用下,也可形 △U=E△l >j=OE成很强的电流。 R= △l 电导率,单位:s/m O△S
❖ 1、欧姆定律的微分形式 由于电流密度可以视为单位面积的电流密度,电场强度可以 视为在电场强度方向单位长度上的电压。 因此,对一段长为 l ,横截面为S的导线,欧姆定律的微分 形式可写成: 实验表明在导电媒质中,当温度不变时,媒质中某点的电流密 度J 与该点的电场强度 E成正比 J E = 欧姆定律的微分形式 l s U I R I J s U E l l R s = = = = J E = 电导率, 单位:s/m 值愈大表明导电能力 愈强,即使在微弱的 电场作用下,也可形 成很强的电流
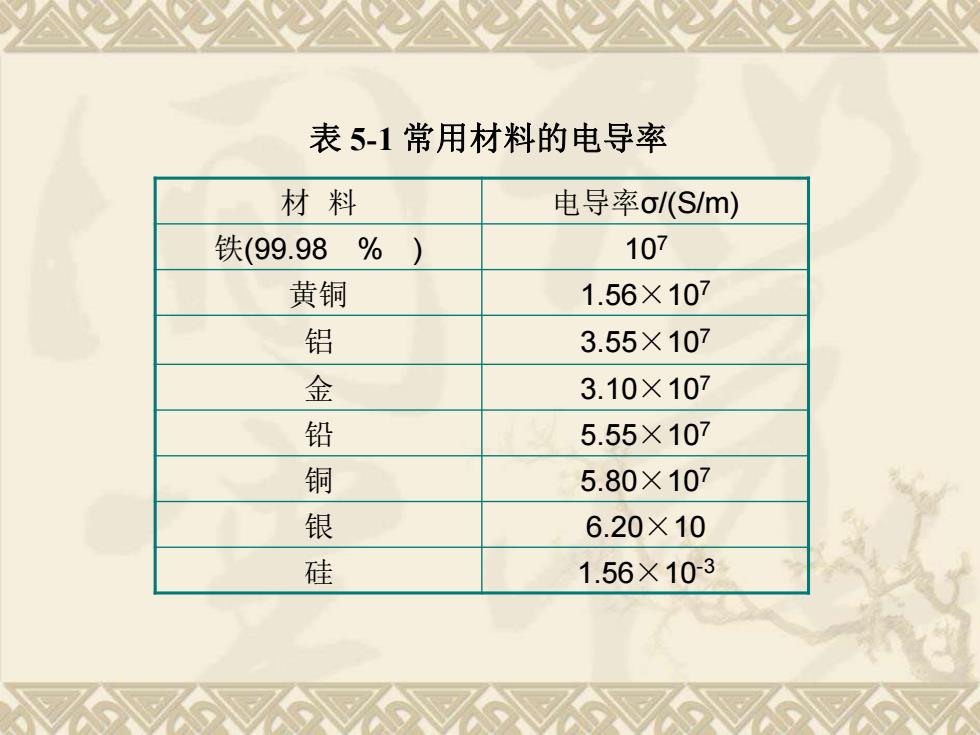
表5-1常用材料的电导率 材料 电导率o/(S/m) 铁(99.98%) 107 黄铜 1.56×107 铝 3.55×107 金 3.10×107 铅 5.55×107 铜 5.80×107 银 6.20×10 硅 1.56×103
材 料 电导率σ/(S/m) 铁(99.98 % ) 107 黄铜 1.56×107 铝 3.55×107 金 3.10×107 铅 5.55×107 铜 5.80×107 银 6.20×10 硅 1.56×10-3 表 5-1 常用材料的电导率

2、焦耳定律的微分形式 当导体两端的电压为U,流过的电流为时,则在单位时间 内电场力对电荷所作的功,即功率是 P=UI 在导体中,沿电流线方向取一长度为△1、截面为△S的体积 元,该体积元内消耗的功率为 △P=△J△I=E△M△I=EJ△l△S=EJ△/
2、 焦耳定律的微分形式 当导体两端的电压为U,流过的电流为I时,则在单位时间 内电场力对电荷所作的功,即功率是 P =UI 在导体中,沿电流线方向取一长度为Δl、截面为ΔS的体积 元,该体积元内消耗的功率为 P = UI = ElI = EJlS = EJV