
《电磁场与电磁波》试题(1)参考答案 二、简答题(每小题5分,共20分) 山,答:意义:随时间变化的磁场可以产生电场。 (3分) 飘分形式5=-爱6 (2分) 12.答:在静电场中,在给定的边界条件下,拉普拉斯方程或泊松方程的解是唯一的,这 定理称为唯一性定理。 (3分) 它的意义:给出了定解的充要条件:既满足方程又满足边界条件的解是正确的。 13.答:电磁波包络或能量的传播速度称为群速。 (3分) 群速v与相速v的关系式为: (2分) 1、0h '。do 4.答位移电流:,-曾 位移电流产生磁效应代表了变化的电场能够产生磁场,使 麦克斯韦能够预言电磁场以波的形式传播,为现代通信打下理论基础。 三、计算题(每小题10分,共30分) 15.按要求完成下列题目 (1)判断矢量函数B=-ye,+x2,是否是某区域的磁通量密度? (2)如果是,求相应的电流分布。 解:(1)根据散度的表达式 尝警是 (3分) 将矢量函数B代入,显然有 7.B=0 (1分) 故:该矢量函数为某区域的磁通量密度。 (1分) (2)电流分布为:
1 《电磁场与电磁波》试题(1)参考答案 二、简答题 (每小题 5 分,共 20 分) 11.答:意义:随时间变化的磁场可以产生电场。 (3 分) 其积分形式为: dS t B E dl C S = − (2 分) 12.答:在静电场中,在给定的边界条件下,拉普拉斯方程或泊松方程的解是唯一的,这一 定理称为唯一性定理。 (3 分) 它的意义:给出了定解的充要条件:既满足方程又满足边界条件的解是正确的。 13.答:电磁波包络或能量的传播速度称为群速。 (3 分) 群速 g v 与相速 p v 的关系式为: d dv v v v p p p g − = 1 (2 分) 14.答:位移电流: t D J d = 位移电流产生磁效应代表了变化的电场能够产生磁场,使 麦克斯韦能够预言电磁场以波的形式传播,为现代通信打下理论基础。 三、计算题 (每小题 10 分,共 30 分) 15.按要求完成下列题目 (1)判断矢量函数 x y B y e ˆ xze ˆ 2 = − + 是否是某区域的磁通量密度? (2)如果是,求相应的电流分布。 解:(1)根据散度的表达式 z B y B x B B x y z + + = (3 分) 将矢量函数 B 代入,显然有 B = 0 (1 分) 故:该矢量函数为某区域的磁通量密度。 (1 分) (2)电流分布为:

J=VxB (2分) 40 (2分) 2 成++] 1分) 16.矢量A=2ex+e,-3e.,B=5e-3说,-e,求 (1)A+B (2)A.B 解:(1)A+B=7e,-2e,-4e (5分) (2)A.B=10-3+3=10 (5分) 17.在无源的自由空间中,电场强度复矢量的表达式为 E=传,3E。-,46k (1)试写出其时间表达式: (2)说明电磁波的传播方向: 解:(1)该电场的时间表达式为:E(,)=Re(Ee) (3分) E(=,1)=(e,3E-e,4Eo)cos(ot-k=) (2分) (2)由于相位因子为e:,其等相位面在xoy平面,传播方向为z轴方向。(5分) 四、应用题(每小题10分,共30分) 18。均匀带电导体球,半径为a,带电量为Q。试求 (1)球内任一点的电场 (2)球外任一点的电位移矢量 解:(1)导体内部没有电荷分布,电荷均匀分布在导体表面,由高斯定理可知在球内处处有: D.ds=0 (3分) 故球内任意一点的电位移矢量均为零,即 (1分) E=0 r<a (1分)
2 ( ) ( 分) ( 分) ( 分) ˆ 2 ˆ 1 1 2 0 ˆ ˆ ˆ 2 1 0 2 0 x z x y z xe y z e y x z x y z e e e J B = − + + − = = 16.矢量 x y ez A = 2e ˆ + e ˆ − 3ˆ , x y z B = 5e ˆ −3e ˆ − e ˆ ,求 (1) A B + (2) A B 解:(1) x y z A+ B = 7e ˆ − 2e ˆ − 4e ˆ (5 分) (2) A B = 10 − 3 + 3 = 10 (5 分) 17.在无源的自由空间中,电场强度复矢量的表达式为 ( ) jkz x y E e E e E e − = 0 − 4 0 ˆ 3 ˆ (1) 试写出其时间表达式; (2) 说明电磁波的传播方向; 解:(1)该电场的时间表达式为: ( ) ( ) j t E z t Ee , = Re (3 分) E(z t) (e E e E ) ( t kz) , = ˆ x3 0 −ˆ y 4 0 cos − (2 分) (2)由于相位因子为 jkz e − ,其等相位面在 xoy 平面,传播方向为 z 轴方向。 (5 分) 四、应用题 (每小题 10 分,共 30 分) 18.均匀带电导体球,半径为 a ,带电量为 Q 。试求 (1) 球内任一点的电场 (2) 球外任一点的电位移矢量 解:(1)导体内部没有电荷分布,电荷均匀分布在导体表面,由高斯定理可知在球内处处有: = 0 S D dS (3 分) 故球内任意一点的电位移矢量均为零,即 (1 分) E = 0 r a (1 分)

(2)由于电荷均匀分布在r=a的导体球面上,故在r>a的球面上的电位移矢量的大小处 处相等,方向为径向,即D=D。e,由高斯定理有 4D.ds=o (3分) 免 4m2D。=0 (1分) 整星可得:D=,=品r>a (1分) 19.设无限长直导线与矩形回路共面,(如图1所示),求 (1)判断通过矩形回路中的磁感应强度的方向(在图中标出): (2)设矩形回路的法向为穿出纸面,求通过矩形回路中的磁通量。 解:建立如图坐标 (1)通过矩形回路中的磁感应强度的方向为穿入纸面,即为毛,方向。 (5分) (2)在x:平面上离直导线距离为x处的磁感应强度可由下式求出: B.di=uol (3分) 即: B=6, (1分) 2 通过矩形回路中的磁通量 w=爪B·s=“了止=h7 d 无穷远 分) 米×× dhb 图2 图1 20.解:(1)由于所求区域无源,电位函数必然满足拉普拉斯方程。 3
3 (2)由于电荷均匀分布在 r = a 的导体球面上,故在 r a 的球面上的电位移矢量的大小处 处相等,方向为径向,即 r D D e ˆ = 0 ,由高斯定理有 D dS Q S = (3 分) 即 r D0 = Q 2 4 (1 分) 整理可得: e ˆ r a r Q D D e ˆ = r = r 0 2 4 (1 分) 19.设无限长直导线与矩形回路共面,(如图 1 所示),求 (1)判断通过矩形回路中的磁感应强度的方向(在图中标出); (2)设矩形回路的法向为穿出纸面,求通过矩形回路中的磁通量。 解:建立如图坐标 (1) 通过矩形回路中的磁感应强度的方向为穿入纸面,即为 y e ˆ 方向。 (5 分) (2) 在 xoz 平面上离直导线距离为 x 处的磁感应强度可由下式求出: = c B dl I 0 (3 分) 即: x I B eˆ y 2 0 = (1 分) 通过矩形回路中的磁通量 d b Ia d dxdz x I B dS d b x d a / S z a / + = = − = + = =− ln 2 2 0 2 2 0 ( 1 分) 20.解:(1)由于所求区域无源,电位函数必然满足拉普拉斯方程。 无穷远 图 2 图 1 x z

设:电位函数为x,y以,则其满足的方程为: p器器-0 (3分) (2)利用分离变量法: x.y)=f(x)g(v) d兰+kf=0 35a0 d (2分) k经+k号=0 根据边界条件=叫=叫,。=0,(,川的通解可写为: 4o.)-n (1分) 再由边界条件: inv. 求得A A-0-s同 (1分) 槽内的电位分布为 k小空器-mh侣宁 五、综合题(10分) 0:照wAE (2分) =是e (2分) %=120z (1分) (2)区域1中反射波电场方向为-毛(3分) 磁场的方向为已, (2分)
4 设:电位函数为 (x, y) ,则其满足的方程为: ( ) 0 2 2 2 2 2 = + = x y x, y (3 分) (2)利用分离变量法: (x, y) = f (x)g(y) 0 0 0 2 2 2 2 2 2 2 2 + = + = + = x y y x k k k g dy d g k f dx d f (2 分) 根据边界条件 0 0 = = = x= x=a y→+ ,(x, y) 的通解可写为: (1 分) 再由边界条件: 求得 An ( nπ) n U An 1 cos 2 0 = − (1 分) 槽内的电位分布为 ( ) ( ) y a n n x e a n nπ n U x, y − = = 1− cos sin 2 1 0 五、综合题 ( 10 分) (1) 21.解:(1) H ez E = ˆ 1 0 (2 分) j z y e E H e − = 0 0 ˆ (2 分) 0 = 120 (1 分) (2) 区域 1 中反射波电场方向为 x − e ˆ (3 分) 磁场的方向为 y e ˆ (2 分) ( ) y a n n n x e a n x y A − = , = sin 1 0 1 0 sin x U a n A n y n = = = =

《电磁场与电磁波》试题(2)参考答案 二、简述题(每小题5分,共20分) 1。答:磁通连续性原理是指:磁感应强度沿任一闭合曲面的积分等于零,或者是从闭合 曲面S穿出去的通量等于由S外流入S内的通量。 (3分) 其数学表达式为:fB·d5=0 (2分) 12。答:当一个矢量场的两类源(标量源和矢量源)在空间的分布确定时,该矢量场就唯一地 确定了,这一规律称为亥姆霍兹定理。 (3分) 亥姆霍兹定理告诉我们,研究任意一个矢量场(如电场、磁场等),需要从散度和旋度 两个方面去研究,或者是从矢量场的通量和环量两个方面去研究。 (2分) 13.答:其物理意义:随时间变化的磁场可以产生电场。(3分) 方程的微分形试xE一爱 (2分) 14.答:电磁波的电场强度矢量的方向随时间变化所描绘的轨迹称为极化。(2分) 极化可以分为:线极化、圆极化、椭圆极化。(3分) 三、计算题(每小题10分,共30分) 15.矢量函数A--x2e,+e,试求 (1)7.a (2)V×A (3分) =-2xy+y (2分) (2) xa品 (3分) -x20 =e:+e.x2 (2分) 16.矢量A=2e,-2e,B=e,-e,求
5 《电磁场与电磁波》试题(2)参考答案 二、简述题 (每小题 5 分,共 20 分) 11. 答:磁通连续性原理是指:磁感应强度沿任一闭合曲面的积分等于零,或者是从闭合 曲面 S 穿出去的通量等于由 S 外流入 S 内的通量。 (3 分) 其数学表达式为: = 0 S B dS (2 分) 12.答:当一个矢量场的两类源(标量源和矢量源)在空间的分布确定时,该矢量场就唯一地 确定了,这一规律称为亥姆霍兹定理。 (3 分) 亥姆霍兹定理告诉我们,研究任意一个矢量场(如电场、磁场等),需要从散度和旋度 两个方面去研究,或者是从矢量场的通量和环量两个方面去研究。 (2 分) 13.答:其物理意义:随时间变化的磁场可以产生电场。 (3 分) 方程的微分形式: t B E = − (2 分) 14.答:电磁波的电场强度矢量的方向随时间变化所描绘的轨迹称为极化。(2 分) 极化可以分为:线极化、圆极化、椭圆极化。(3 分) 三、计算题 (每小题 10 分,共 30 分) 15.矢量函数 x z A yx e ˆ yze ˆ 2 = − + ,试求 (1) A (2) A 解:(1) ( 分) ( 分) 2 2 3 x y y z A y A x A A x y z = − + + + = (2) ( 分) 分) ˆ ˆ 2 (3 0 ˆ ˆ ˆ 2 2 e z e x yx yz x y z e e e A x z x y z = + − = 16.矢量 x z A = 2e ˆ − 2e ˆ , x y B = e ˆ − e ˆ ,求

(1)A-B (2)求出两矢量的夹角 解:(1) a-B=2e-2e.-e,-e,) (3分) =e,+e,-2e (2分) (2)根据A,B=ABcos0 (2分) 4.B=(2e-2e)e-e,)=2 cos8=2252 21 (2分) 所以0=60° (1分) n.解ww=60+g+e是 3分) =e2x+e,2y+e.2: (2分) ai岛 (2分) 装8 (3分) 四、应用题(每小题10分,共30分) 18。放在坐标原点的点电荷在空间任一点F处产生的电场强度表达式为 (1)求出电力线方程:(2)画出电力线。 由力线方程得 本正 (2分) 对上式积分得 y=Cx (1分) :=C3y 6
6 (1) A B − (2)求出两矢量的夹角 解:(1) ( ) ( 分) 分) ˆ ˆ 2ˆ 2 2ˆ 2ˆ ˆ ˆ (3 x y z x z x y e e e A B e e e e = + − − = − − − (2)根据 A B = ABcos (2 分) A B = (2e ˆ x − 2e ˆ z )(e ˆ x − e ˆ y ) = 2 2 1 2 2 2 2 cos = = (2 分) 所以 = 60 (1 分) 17.解:(1) ( 分) ( 分) ˆ 2 ˆ 2 ˆ 2 2 ˆ ˆ ˆ 3 e x e y e z z u e y u e x u u e x y z x y z = + + + + = (2) u u n ˆ = (2 分) 所以 5 ˆ ˆ 2 4 16 ˆ 2 ˆ 4 ˆ x y x y e e e e n + = + + = (3 分) 四、应用题 (每小题 10 分,共 30 分) 18.放在坐标原点的点电荷在空间任一点 r 处产生的电场强度表达式为 r e r q E ˆ 4 2 0 = (1)求出电力线方程;(2)画出电力线。 解:(1) (e x e y e z) r q r qr e r q E r x y z ˆ ˆ ˆ 4 4 ˆ 4 3 0 3 0 2 0 = = = + + (2 分) 由力线方程得 dz z dy y dx x = = (2 分) 对上式积分得 z C y y C x 2 1 = = (1 分)
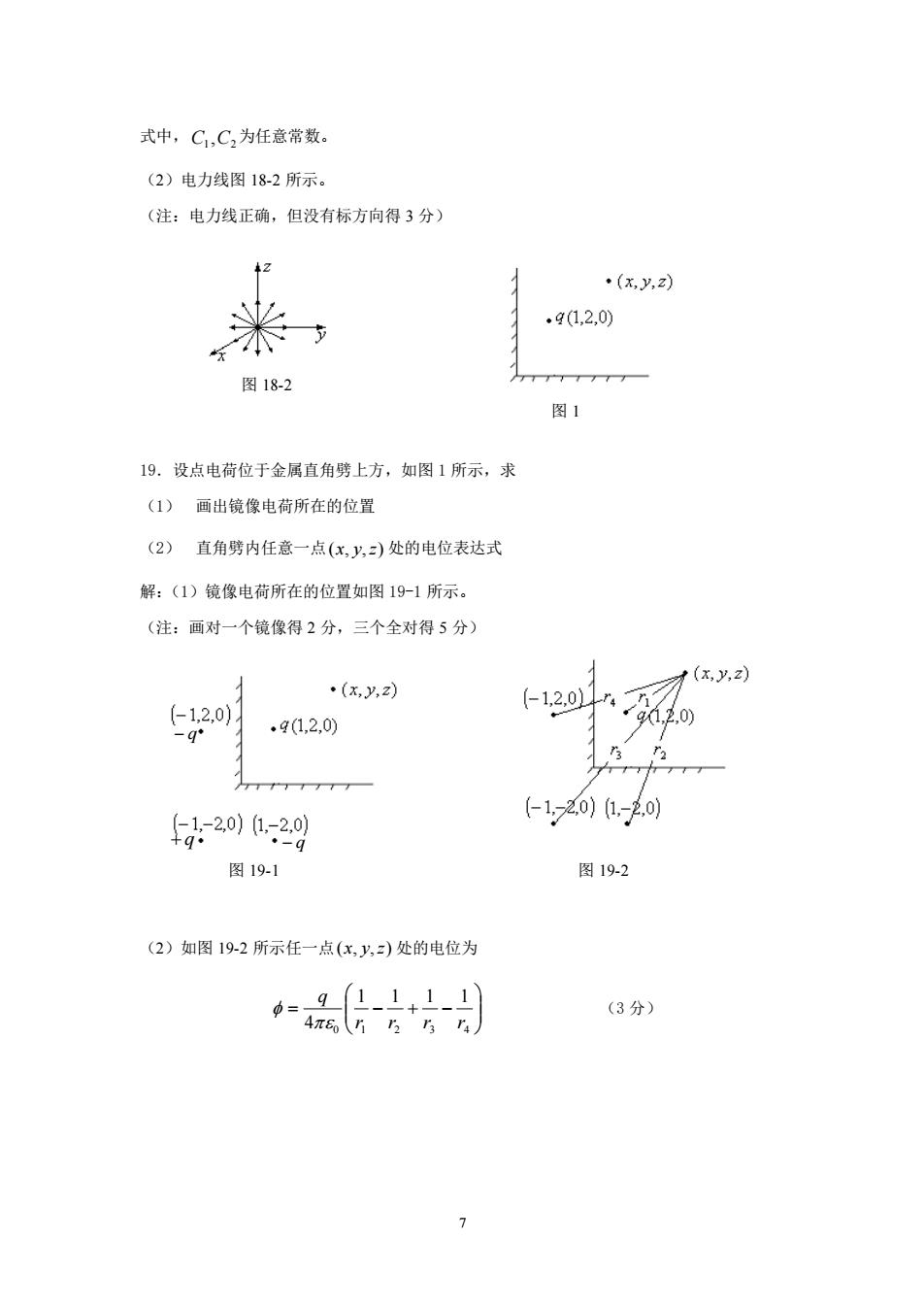
式中,C,C,为任意常数 (2)电力线图18-2所示。 (注:电力线正确,但没有标方向得3分) ·(xy,z) 米 .g1.2.0) 图18-2 图1 19.设点电荷位于金属直角劈上方,如图1所示,求 (1)画出镜像电荷所在的位置 (2)直角劈内任意一点(x,y,)处的电位表达式 解:(1)镜像电荷所在的位置如图19-1所示。 (注:画对一个镜像得2分,三个全对得5分) ·(x,y,z) (-1.2.0) -q .g1,2.0 20:2g 10).o 图19-1 图19-2 (2)如图19-2所示任一点(x,八,)处的电位为 品+6动 (3分) >
7 式中, 1 2 C ,C 为任意常数。 (2)电力线图 18-2 所示。 (注:电力线正确,但没有标方向得 3 分) 19.设点电荷位于金属直角劈上方,如图 1 所示,求 (1) 画出镜像电荷所在的位置 (2) 直角劈内任意一点 (x, y,z) 处的电位表达式 解:(1)镜像电荷所在的位置如图 19-1 所示。 (注:画对一个镜像得 2 分,三个全对得 5 分) (2)如图 19-2 所示任一点 (x, y,z) 处的电位为 = − + − 0 1 2 3 4 1 1 1 1 4 r r r r q (3 分) 图 1 图 18-2 图 19-1 图 19-2 + q − q − q

r=V-+0-2+ 其中,5=-少+0+2沙+ (2分) 5=V+1+0y+2+z r=Vx+12+0-2+ 20.设时变电磁场的电场强度和磁场强度分别为: E=E。cos(ot-中.) 月=i。cos(ot-pn) (1)写出电场强度和磁场强度的复数表达式 (2)证明其坡印廷矢量的平均值为:S.=)E。×,c0s(。-a) 解:(1)电场强度的复数表达式 E=Ee-Ite (3分) 电场强度的复数表达式 H=Hoe1 (2分) (2)根据 5=Re医x月)e (2分) Sn=Re民,×A,e小xco0.-4.) (3分) 五、综合题(共10分) 21,设沿+:方向传播的均匀平面电磁波垂直入射到理想导体,如图2所示,该电磁波电场 只有x分量即E=e,E。em (②)求出反射波电场的表达式: (3)求出区域1媒质的波阻抗。 月。传举方向 ,气 理想导体 解:(1)设反射波电场 区域1 区域2 E=e,Ee 图2 区域1中的总电场为 E+E =e,(Ee+Ee) (2分) 根据:=0导体表面电场的切向分量等于零的边界条件得
8 其中, ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 4 2 2 2 3 2 2 2 2 2 2 2 1 1 2 1 2 1 2 1 2 r x y z r x y z r x y z r x y z = + + − + = + + + + = − + + + = − + − + (2 分) 20.设时变电磁场的电场强度和磁场强度分别为: cos( ) 0 e E = E t − cos( ) 0 m H = H t − (1) 写出电场强度和磁场强度的复数表达式 (2) 证明其坡印廷矢量的平均值为: cos( ) 2 1 Sav = E0 H0 e − m 解:(1)电场强度的复数表达式 e j E E e − = 0 (3 分) 电场强度的复数表达式 j m H H e − = 0 (2 分) (2)根据 ( ) * Re 2 1 Sav E H = 得 (2 分) ( ) cos( ) 2 1 Re 2 1 0 0 ( ) 0 0 e m j e m Sa v E H e E H = = − − − (3 分) 五、综合题 (共 10 分) 21.设沿 + z 方向传播的均匀平面电磁波垂直入射到理想导体,如图 2 所示,该电磁波电场 只有 x 分量即 j z x E e E e − = 0 ˆ (2) 求出反射波电场的表达式; (3) 求出区域 1 媒质的波阻抗。 解:(1)设反射波电场 j z r x r E e E e = ˆ 区域 1 中的总电场为 ˆ ( ) 0 j z r j z r x E E e E e E e + = + − (2 分) 根据 z = 0 导体表面电场的切向分量等于零的边界条件得 区域 1 区域 2 图 2

E.=-E (2分) 因此,反射波电场的表达式为 E,=-Eoe (1分) (2)媒质1的波阻抗 = (3分) 因而得n=120r=377(2) (2分) 《电磁场与电磁波》试题(3)参考答案 二、简述题(每小题5分,共20分) 山。答:它表明时变场中的腿场是由传导电流了和位移电流D共同产生3分。 该方程的积分形式为 (2分) 12.答:与传播方向垂直的平面称为横向平面:(1分) 电磁场E和H的分量都在横向平面中,则称这种波称为平面波:(2分) 在其横向平面中场值的大小和方向都不变的平面波为均匀平面波。(2分) 13。答:静电场为无旋场,故沿任何闭合路径的积分为零:或指出静电场为有势场、保守场 静电场的两个基本方程积分形式: {D.&=q fE.di=0 或微分形式 V×E=0 V.D=p 两者写出一组即可,每个方程1分。 9
9 Er = −E0 (2 分) 因此,反射波电场的表达式为 j z r x E e E e 0 = −ˆ (1 分) (2)媒质 1 的波阻抗 0 0 = (3 分) 因而得 = 120 = 377() (2 分) 《电磁场与电磁波》试题(3)参考答案 二、简述题 (每小题 5 分,共 20 分) 11.答:它表明时变场中的磁场是由传导电流 J 和位移电流 t D 共同产生(3 分)。 该方程的积分形式为 dS t D H dl J C S = + (2 分) 12. 答:与传播方向垂直的平面称为横向平面;(1 分) 电磁场 E和H 的分量都在横向平面中,则称这种波称为平面波;(2 分) 在其横向平面中场值的大小和方向都不变的平面波为均匀平面波。(2 分) 13.答:静电场为无旋场,故沿任何闭合路径的积分为零;或指出静电场为有势场、保守场 静电场的两个基本方程积分形式: = S D dS q = 0 l E dl 或微分形式 E = 0 D = 两者写出一组即可,每个方程 1 分

14.答: V2d=-py IE (3分) 它表示求解区域的电位分布仅决定于当地的电荷分布。(2分) 三、计算题(每小题10分,共30分) 5.用球坐标表示的场E=心,兰,求 (1)在直角坐标中点(-3,4,5)处的E: (2)在直角坐标中点(-3,4,5)处的E分量 解: (1)在直角坐标中点(-3,4,5)在球坐标中的矢径大小为: r=V(-3}+42+52=52 (2分) 故该处的电场大小为: 4=草号 (3分) (2)将球坐标中的场表示为 6- (2分) 将r=52,x=-3代入上式即得: 6=9 (1分) 16.矢量函数A=-xe+e,+xe,试求 (1)V.A (2)若在y平面上有一边长为2的正方形,且正方形的中心在坐标原点,试求该矢量A穿 过此正方形的通量。 解: (1)
10 14.答: / 2 = − V (3 分) 它表示求解区域的电位分布仅决定于当地的电荷分布。(2 分) 三、计算题 (每小题 10 分,共 30 分) 15.用球坐标表示的场 2 25 ˆ r E e = r ,求 (1) 在直角坐标中点(-3,4,5)处的 E ; (2) 在直角坐标中点(-3,4,5)处的 Ex 分量 解: (1)在直角坐标中点(-3,4,5)在球坐标中的矢径大小为: ( 3) 4 5 5 2 2 2 2 r = − + + = (2 分) 故该处的电场大小为: 2 25 1 2 = = r E (3 分) (2)将球坐标中的场表示为 ( ) r x y z xe ˆ ye ˆ ze ˆ r r r r E = e ˆ = = + + 2 3 3 25 25 25 (2 分) 故 3 25 r x Ex = (2 分) 将 r = 5 2 , x = −3 代入上式即得: 20 3 2 Ex = − (1 分) 16.矢量函数 x y z A x e ˆ ye ˆ xe ˆ 2 = − + + ,试求 (1) A (2)若在 xy 平面上有一边长为 2 的正方形,且正方形的中心在坐标原点,试求该矢量 A 穿 过此正方形的通量。 解: (1)