
第六章 静电学
第六章 静电学

§2一1电场 电场强 一、库仑定囊 F=k9192 式中为比例系数,飞=9.0×10NmC-2,常 写做k= 一,6为真空介电常数, 4元 6。=885×102C2Nm2则库仑定律为: F- 1 4元Eo
§2-1 电场 电场强 度 一、库仑定律 1 2 2 q q F k r = 式中 为比例系数, =9.0109Nm2C-2,常 写做 , 为真空介电常数, 则库仑定律为: k k 0 1 4 k = 0 12 2 1 2 0 8.85 10 C N m − − − = 1 2 2 0 1 4 q q F r =

二、电场和电场强度 只讨论相对观察者静止的电荷所产生 的电场,即静电场。 电场强度定义为: E= 场强的单位是N/C,也可用Vm
二、电场和电场强度 0 F E q = 场强的单位是N/C,也可用V/m。 只讨论相对观察者静止的电荷所产生 的电场,即静电场。 电场强度定义为:
三、场强叠加原理 1、点电荷的场强 如图,q在电场中受到的电场力为: 1 4π6。 如果场源的电荷O为正,场强E的 方向沿r向外;如果场源电荷Q为 负,场强E的方向沿r指向Q
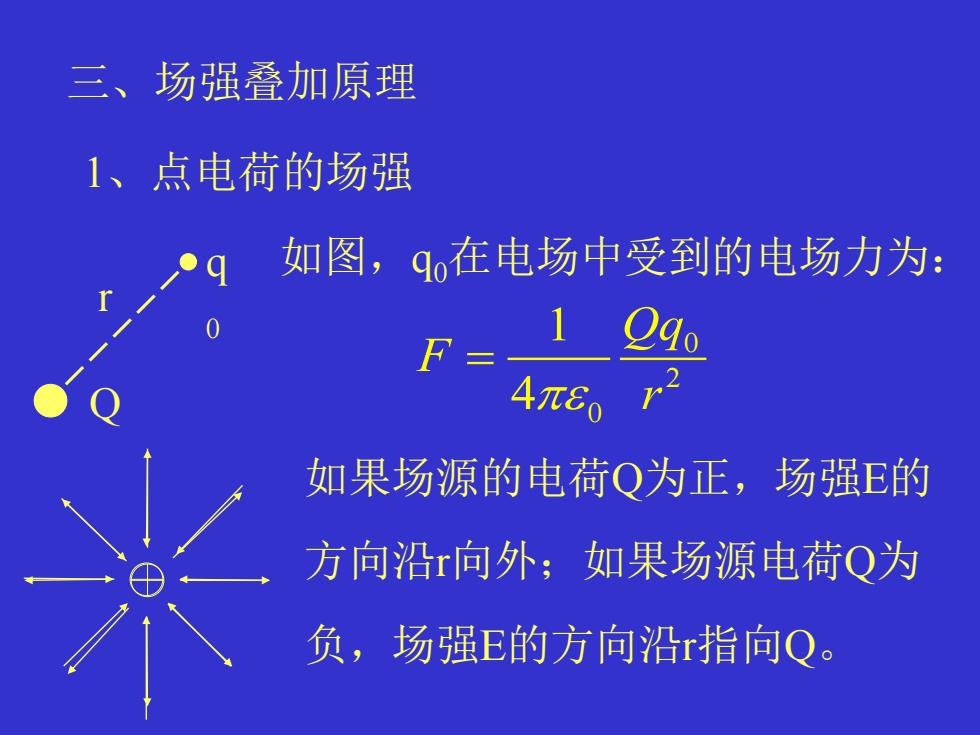
三、场强叠加原理 1、点电荷的场强 Q q 0 r 如图,q0在电场中受到的电场力为: 0 2 0 1 4 Qq F r = 如果场源的电荷Q为正,场强E的 方向沿r向外;如果场源电荷Q为 负,场强E的方向沿r指向Q

场强可用矢量式表示,用.表示 矢径,其方向沿r由Q指向qo,用 表示方向上的单位矢量,则 r =rro 因此点电荷的场强矢量式为: E-
场强可用矢量式表示,用 表示 矢径,其方向沿 r 由Q指向q0,用 表示 方向上的单位矢量,则 r 0 r r 0 r rr = 因此点电荷的场强矢量式为: 2 0 0 1 4 Q E r r =
2、点电荷系(组)的场强 场强叠加原理 90 由n个点电荷q、g2.9n构成的 E 点电荷系(组)。用R、EF 分别表示4、92..9n对9的作用 力,F表示F、互F的矢量和, 则: F=五+F++F
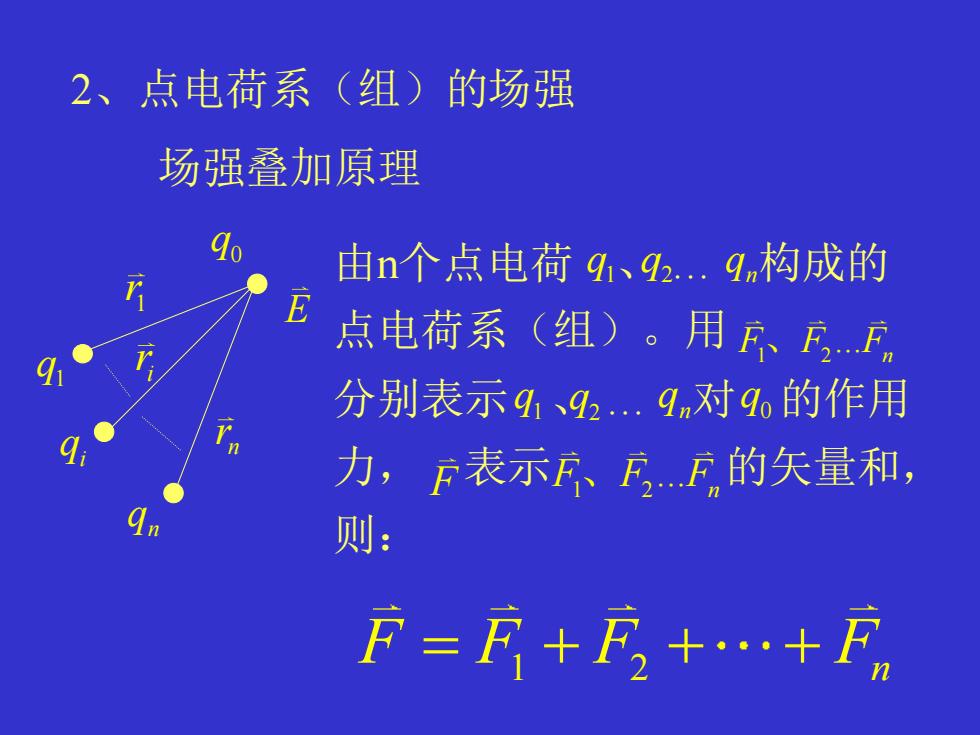
2、点电荷系(组)的场强 场强叠加原理 E 0 q 1 r n r i r 1 q i q n q F F F F = + + + 1 2 n 由n个点电荷 、 … 构成的 点电荷系(组)。用 分别表示 、 … 对 的作用 力, 表示 的矢量和, 则: 1 q 2 q n q 1 2... F F F 、 n 1 q 2 q n q 0 q 1 2... F F F F 、 n

两边同时除以4,得: F-F ++ 90 显然F为总场强,用E表示,右边多项式分别 是各场源点电荷的场强,用E、E,…E表示, 则上式变为: E=E+E++En=∑E
两边同时除以 q0 ,得: 1 2 0 0 0 0 F F F F n q q q q = + + + 显然 为总场强,用 表示,右边多项式分别 是各场源点电荷的场强,用 表示, 则上式变为: 0 F q E E E E 1 2 、 n 1 2 n i i E E E E E = + + + = (或 2 0 ) 0 1 4 i i q r r =

3、电荷连续分布的带电体的场强 I、首先,将带电体分成无数个小 电荷元dg,然后求出任一电荷元 dg在某点的场强dE一一微分过程 dE 1 dq 4πr1 Ⅱ、其次,把所有电荷元在该点的场强矢量 叠加起来,求出带电体在该点的场强一一积 分过程,即应用叠加原理 E-jk-∫曾6
3、电荷连续分布的带电体的场强 I、首先,将带电体分成无数个小 电荷元 ,然后求出任一电荷元 在某点的场强 --微分过程 dq dq dE 2 0 0 1 4 dq dE r r = II、其次,把所有电荷元在该点的场强矢量 叠加起来,求出带电体在该点的场强--积 分过程,即应用叠加原理 2 0 0 1 4 dq E dE r r = =

例2-1 如图,一半径为a的均匀带电圆环, 带电量为g。计算在环轴线上距环 心x处的P点的场强。 dl 解:取轴线为x轴,单位长度 圆环带电量称为线电荷密 度,用入表示,则 dE 2πa 在环上取一线元d,则线元d所带的电荷的电 量为 dg=λdl=
例2-1 如图,一半径为a的均匀带电圆环, 带电量为q。计算在环轴线上距环 心x处的P点的场强。 dl x dEx x a O q r P dE 解:取轴线为x轴,单位长度 圆环带电量称为线电荷密 度,用表示,则 2 q a = 在环上取一线元dl,则线元dl所带的电荷的电 量为 2 q dq dl dl a = =

电荷元dg在P点的场强为 dE 1 dq 方向如图 4π8ò 式中r√a2+x2 将dE分解成沿轴线的x方向分量dE,和垂直轴线 的y方向分量dE,dE互相抵消,因此dE=O。 所以P点的场强应为各电荷元x方向场强分量的 叠加 .dE,=dEcose cos0= +x dE dq xdq cos0 4π8 4E(a2+x2形
电荷元dq在P点的场强为 2 0 1 4 dq dE r = 方向如图 式中r = 2 2 a x + 将dE分解成沿轴线的x方向分量dEx和垂直轴线 的y方向分量dEy, dEy互相抵消,因此dEy =0。 所以P点的场强应为各电荷元x方向场强分量的 叠加 2 2 cos cos x x x dE dE r a x = = = + 2 3 2 2 2 0 0 1 1 cos 4 4 ( ) x dq xdq dE r a x = = +