
质点力学检测题 5 一、填空题: 1、图a中ac曲线为抛物线的一部分,是作直线运动的质点 位置随时间的关系曲线,曲线在a点处的切线通过(1,3) 点。 (1)在图b中画出质点的-‘图线,在图c中画出质点的 a-t图线: (2)该质点的运动方程。 2、质点沿路径5运动,在P点的位置矢量为护,速度为P, 2 加速度为4,如图所示。 (b) 则在该点: 的 (e) 0= 3、如图所示装置,饶0轴转动的定滑轮,半径为R=01米 设重物州下落的规律为:y=32+5(4以秒计,X以米 计),则时刻: (1)重物m的速度矢量立= 加速度矢量云= 题2图 (2)距离0轴2“处轮上P点的速度心= ,加
质点力学检测题 一、填空题: 1、图 a 中 曲线为抛物线的一部分,是作直线运动的质点 位置随时间的关系曲线,曲线在 a 点处的切线通过(1,3) 点。 (1)在图 b 中画出质点的 图线,在图 c 中画出质点的 图线; (2)该质点的运动方程 :___________________。 2、质点沿路径 运动,在 P 点的位置矢量为 ,速度为 , 加速度为 ,如图所示。 则在该点: ___________; ___________; _________; _________。 3、如图所示装置,饶 O 轴转动的定滑轮,半径为 米, 设重物 下落的规律为: ( 以秒计, 以米 计),则 时刻: (1)重物 的速度矢量 ____________,加速度矢量 _______________; (2)距离 O 轴 处轮上 P 点的速度 _____________,加

速度矢量在= 1日 题3图 4、质量为m的小球,用长为的细线悬挂在车顶上,当车厢相对地面的加速度为0 时,车内观察到小球在日位置时向下摆动的速度为口。以车厢为参考系: (1)在图上画出小球受到的作用力: (2)绳子张力1= 一,小球的切向加速度,= 777777 题4图 题5图 5、作用在质点上的力为=属cos矿,式中:年为切向单位矢量,P为牵引力京与水平 方向小于2的夹角。设质点从0点沿如图所示路径运动到B点,力疗所作的功A= 一,该力是否保守力 一,其理由是 6、质量州=2g的质点处于如图所示的一维势场中,开始时质点位于X=7m处,以初 速8=-2运动,则: (1)该粒子的运动范围为: (2)粒子受到正向斥力范围为: (3)粒子在x= _处的速率最大,其最大速率为
速度矢量 _____________。 4、质量为 的小球,用长为 的细线悬挂在车顶上,当车厢相对地面的加速度为 时,车内观察到小球在 位置时向下摆动的速度为 。以车厢为参考系: (1)在图上画出小球受到的作用力; (2)绳子张力 T=____________,小球的切向加速度 ____________。 5、作用在质点上的力为 ,式中: 为切向单位矢量, 为牵引力 与水平 方向小于 的夹角。设质点从 O 点沿如图所示路径 运动到 B 点,力 所作的功 ___________,该力是否保守力____________,其理由是_________________。 6、质量 的质点处于如图所示的一维势场中,开始时质 点位于 处,以初 速 运动,则: (1)该粒子的运动范围为: ________________________________; (2)粒子受到正向斥力范围为: ________________________________; (3)粒子在 ____________处的速率最大,其最大速率为______________
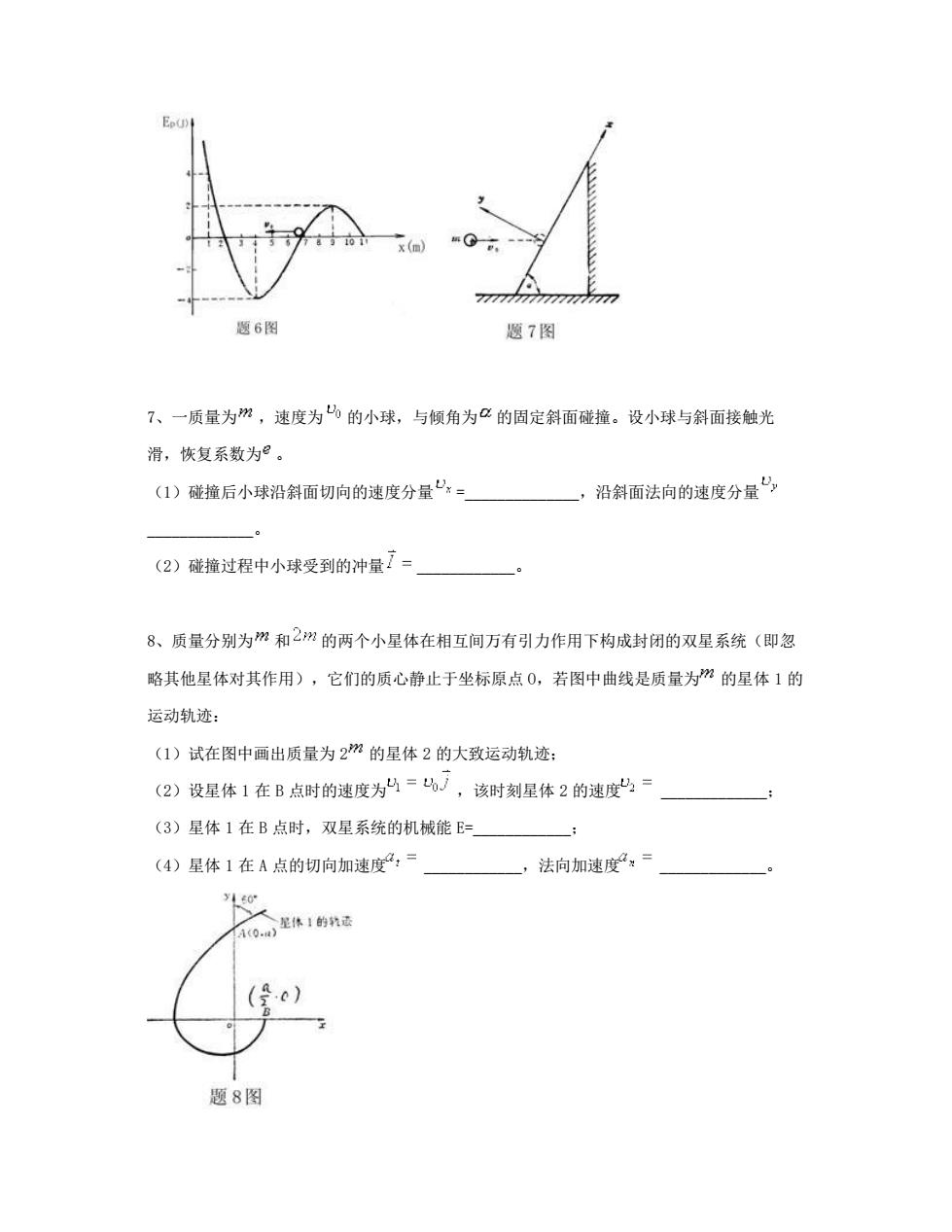
题6图 题7图 7、一质量为m,速度为的小球,与倾角为2的固定斜面碰撞。设小球与斜面接触光 滑,恢复系数为°。 (1)碰撞后小球沿斜面切向的速度分量:- 一,沿斜面法向的速度分量 (2)碰撞过程中小球受到的冲量7= 8、质量分别为m和2现的两个小星体在相互间万有引力作用下构成封闭的双星系统(即忽 略其他星体对其作用),它们的质心静止于坐标原点0,若图中曲线是质量为m的星体1的 运动轨迹: (1)试在图中画出质量为2m的星体2的大致运动轨迹: (2)设星体1在B点时的速度为=了,该时刻星体2的速度,=」 (3)星体1在B点时,双星系统的机械能E= (4)星体1在A点的切向加速度,= 一,法向加速度。 0,星1的运 题8图
7、一质量为 ,速度为 的小球,与倾角为 的固定斜面碰撞。设小球与斜面接触光 滑,恢复系数为 。 (1)碰撞后小球沿斜面切向的速度分量 =______________,沿斜面法向的速度分量 _____________。 (2)碰撞过程中小球受到的冲量 ____________。 8、质量分别为 和 的两个小星体在相互间万有引力作用下构成封闭的双星系统(即忽 略其他星体对其作用),它们的质心静止于坐标原点 O,若图中曲线是质量为 的星体 1 的 运动轨迹: (1)试在图中画出质量为 2 的星体 2 的大致运动轨迹; (2)设星体 1 在 B 点时的速度为 ,该时刻星体 2 的速度 _____________; (3)星体 1 在 B 点时,双星系统的机械能 E=____________; (4)星体 1 在 A 点的切向加速度 ____________,法向加速度 _____________

三、计算题: 1、c是一立交桥面,桥面中部区间按》=H-x的规律变化。若一质最为m的汽车驶 过桥面时,保持不方向的分速度“,=”不变,试计算汽车在桥中部区间任一点的: (1)速度矢量和加速度矢量: (2)切向加速度和法向加速度。 777777 0A 题1图 题2图 2、在如图所示的连接体中,己知物体A与滑块B的质量分别为”和M,滑轮与绳的质量均 不计,且绳无伸长,该机构仅在滑块与物体之间有摩擦,摩擦系数为“。 (1)画出物体A和滑块B的隔离体受力图: (2)计算物体A和滑块B相对地面的加速度。 3、一质量为M的机动船,在进入河弯道前Q点处关闭发动机,以速度在静水中行驶,设 水的阻力与船速成正比,且方向相反,比例系数为k。 (1)若Q点至弯道处P点的距离为0,求船行至P点时的速率: (2)若船行至P点时开动发动机,给船以品的转向力,品与速度方向的夹角为口,如图 所示,则求船在该点的切向加速度及航道的曲率半径
二、计算题: 1、 是一立交桥面,桥面中部区间按 的规律变化。若一质量为 的汽车驶 过桥面时,保持 方向的分速度 不变,试计算汽车在桥中部区间任一点的: (1)速度矢量和加速度矢量; (2)切向加速度和法向加速度。 2、在如图所示的连接体中,已知物体 A 与滑块 B 的质量分别为 和 M,滑轮与绳的质量均 不计,且绳无伸长,该机构仅在滑块与物体之间有摩擦,摩擦系数为 。 (1)画出物体 A 和滑块 B 的隔离体受力图; (2)计算物体 A 和滑块 B 相对地面的加速度。 3、一质量为 M 的机动船,在进入河弯道前 Q 点处关闭发动机,以速度 在静水中行驶,设 水的阻力与船速成正比,且方向相反,比例系数为 。 (1)若 Q 点至弯道处 P 点的距离为 ,求船行至 P 点时的速率 ; (2)若船行至 P 点时开动发动机,给船以 的转向力, 与速度方向的夹角为 ,如图 所示,则求船在该点的切向加速度及航道的曲率半径

题3图 题4图 4、图为浮在一种液体中的木块,木块长为,质量为M,平衡时木块三分之二部分浸在液体 里。现有质量为州的小球,以速度沿8=60'方向与木块碰撞。设木块与小球之间光 滑,恢复系数。三言。=4,试求 (1)碰撞后瞬时小球速度的水平和竖直分量值: (2)要使木块能够全部沉入液体,小球的初速度至少应为多大。 质点力学检测题 9 答案 一、1、 2号=a5万 )2 p asmn月 3、)0=6面,a=6行20=对,a=3j+180行 4、(2 T=m3c088+m,78+ i,a,=gsm日-a。cos6 5、4=风b,不是京0 6、(1)x21(2)1≤x≤4:(3)x=4,4=22m1e 7、4)“,=场co8,马=e场m6 (2)7=m61+e)sm香 a时-og 4Gm 43 Gm (4)9a:9a2
4、图为浮在一种液体中的木块,木块长为 ,质量为 M,平衡时木块三分之二部分浸在液体 里。现有质量为 的小球,以速度 沿 方向与木块碰撞。设木块与小球之间光 滑,恢复系数 , ,试求: (1)碰撞后瞬时小球速度的水平和竖直分量值; (2)要使木块能够全部沉入液体,小球的初速度 至少应为多大。 质点力学检测题 答案 一、1、 2、 , , , 3、(1) , (2) , 4、(2) , 5、 ,不是 6、(1) ;(2) ;(3) ; 7、(1) ; (2) 8、(2) (3) (4) ; 二

42x2 2Kv2 1、D0=f-2x5.a=-2方2) +原,+ g.+wf-刀.++w mg 松g Fsin a (2)%=V6g@
1、( 1 ) ; ( 2 ) ; 2 、 ; 3、( 1 ) ( 2 ) , 4、( 1 ) ; ( 2 )
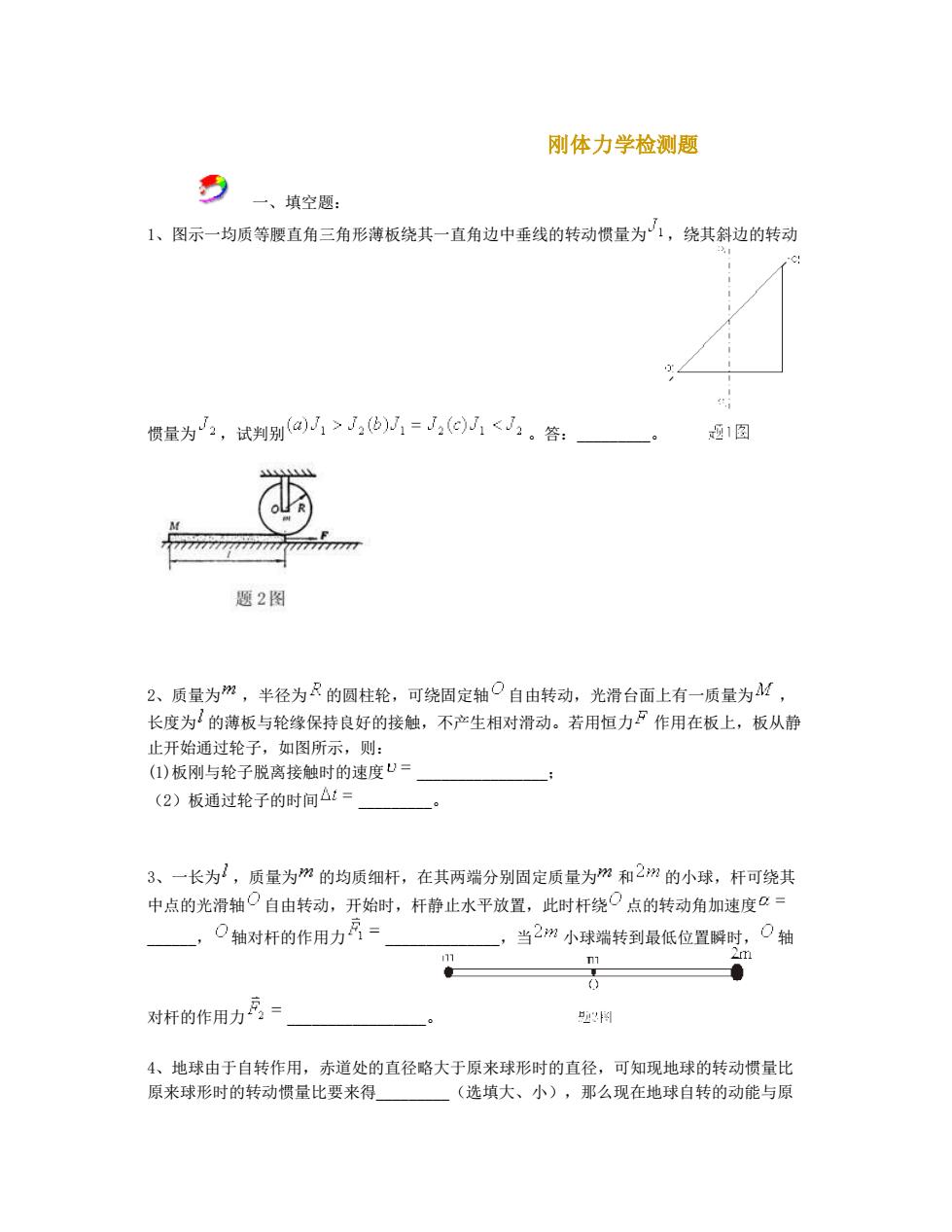
刚体力学检测题 一、填空题: 1、图示一均质等腰直角三角形薄板绕其一直角边中垂线的转动惯量为1,绕其斜边的转动 惯量为,试判别@山>,@以=J,(e从<,.答 通1图 题2图 2、质量为州,半径为R的圆柱轮,可绕固定轴O自由转动,光滑台面上有一质量为4, 长度为的薄板与轮缘保持良好的接触,不产生相对滑动。若用恒力户作用在板上,板从静 止开始通过轮子,如图所示,则: ()板刚与轮子脱离接触时的速度U= (2)板通过轮子的时间△1= -0 3、一长为2,质量为m的均质细杆,在其两端分别固定质量为m和2m的小球,杆可绕其 中点的光滑轴Q自由转动,开始时,杆静止水平放置,此时杆绕Q点的转动角加速度C= 一,○轴对杆的作用力况=】 一,当2州小球端转到最低位置瞬时,0轴 0 对杆的作用力乃三 剧 4、地球由于自转作用,赤道处的直径略大于原来球形时的直径,可知现地球的转动惯量比 原来球形时的转动惯量比要来得 (选填大、小),那么现在地球自转的动能与原
刚体力学检测题 一、填空题: 1、图示一均质等腰直角三角形薄板绕其一直角边中垂线的转动惯量为 ,绕其斜边的转动 惯量为 ,试判别 。答:_________。 2、质量为 ,半径为 的圆柱轮,可绕固定轴 自由转动,光滑台面上有一质量为 , 长度为 的薄板与轮缘保持良好的接触,不产生相对滑动。若用恒力 作用在板上,板从静 止开始通过轮子,如图所示,则: (1)板刚与轮子脱离接触时的速度 ________________; (2)板通过轮子的时间 _________。 3、一长为 ,质量为 的均质细杆,在其两端分别固定质量为 和 的小球,杆可绕其 中点的光滑轴 自由转动,开始时,杆静止水平放置,此时杆绕 点的转动角加速度 ______, 轴对杆的作用力 ______________,当 小球端转到最低位置瞬时, 轴 对杆的作用力 _________________。 4、地球由于自转作用,赤道处的直径略大于原来球形时的直径,可知现地球的转动惯量比 原来球形时的转动惯量比要来得_________(选填大、小),那么现在地球自转的动能与原
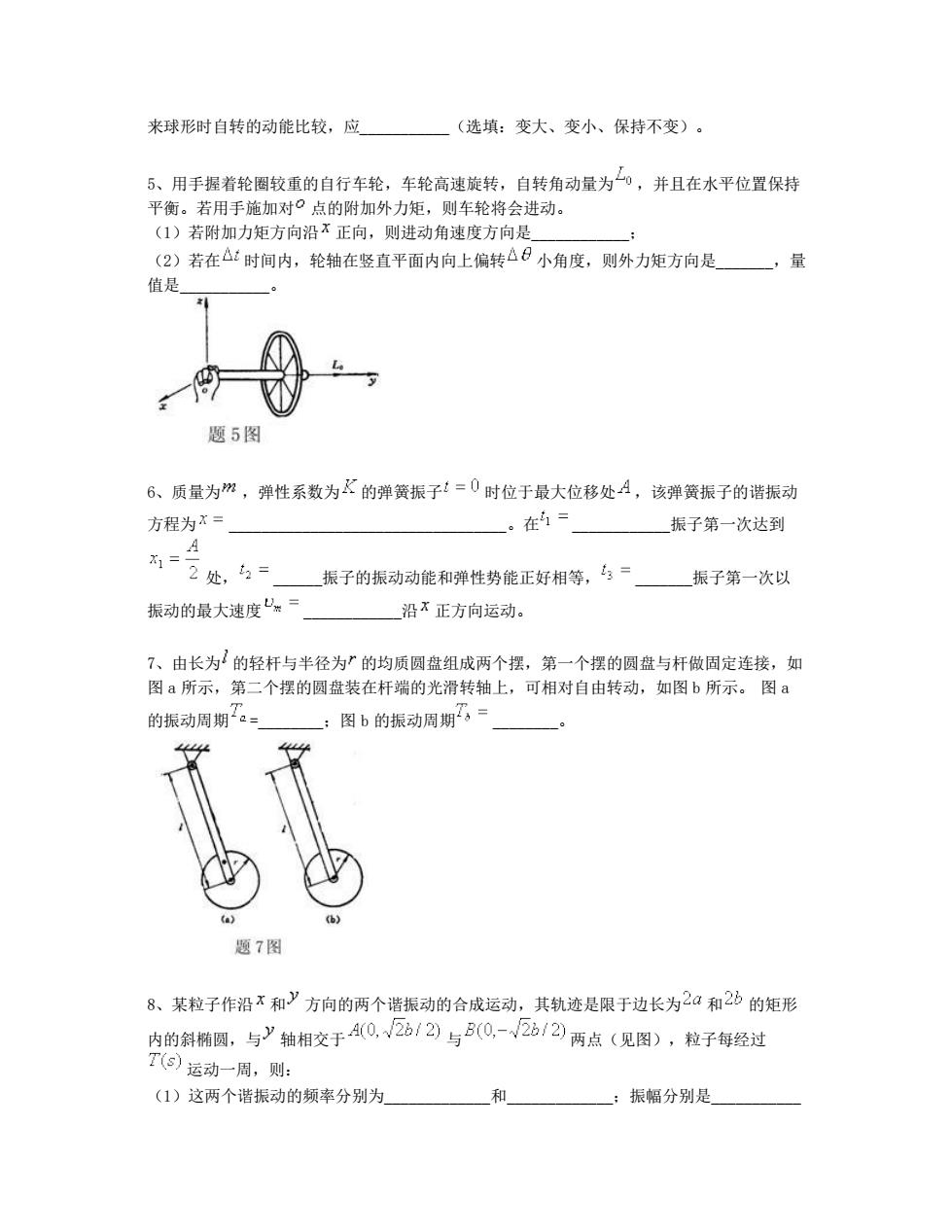
来球形时自转的动能比较,应一(选填:变大、变小、保持不变)。 5、用手握着轮圈较重的自行车轮,车轮高速旋转,自转角动量为0,并且在水平位置保持 平衡。若用手施加对口点的附加外力矩,则车轮将会进动。 (1)若附加力矩方向沿不正向,则进动角速度方向是 (2)若在△:时间内,轮轴在竖直平面内向上偏转△日小角度,则外力矩方向是,量 值是 题5图 6、质量为m,弹性系数为K的弹簧振子!=0时位于最大位移处A,该弹簧振子的谐振动 方程为X= 。在1 振子第一次达到 2处,= 振子的振动动能和弹性势能正好相等,= 振子第一次以 振动的最大速度 沿正方向运动。 7、由长为的轻杆与半径为的均质圆盘组成两个摆,第一个摆的圆盘与杆做固定连接,如 图a所示,第二个摆的圆盘装在杆端的光滑转轴上,可相对自由转动,如图b所示。图a 的振动周期a= 图b的振动周期= 题7图 8、某粒子作沿不和'方向的两个谐振动的合成运动,其轨迹是限于边长为2和2b的矩形 内的斜椭圆,与'轴相交于0.26/2与5(0,-2/②两点(见图),粒子每经过 1⊙运动一周,则: (1)这两个谐振动的频率分别为 、和 ;振幅分别是
来球形时自转的动能比较,应___________(选填:变大、变小、保持不变)。 5、用手握着轮圈较重的自行车轮,车轮高速旋转,自转角动量为 ,并且在水平位置保持 平衡。若用手施加对 点的附加外力矩,则车轮将会进动。 (1)若附加力矩方向沿 正向,则进动角速度方向是____________; (2)若在 时间内,轮轴在竖直平面内向上偏转 小角度,则外力矩方向是_______,量 值是___________。 6、质量为 ,弹性系数为 的弹簧振子 时位于最大位移处 ,该弹簧振子的谐振动 方程为 __________________________________。在 ____________振子第一次达到 处, ______振子的振动动能和弹性势能正好相等, _______振子第一次以 振动的最大速度 ____________沿 正方向运动。 7、由长为 的轻杆与半径为 的均质圆盘组成两个摆,第一个摆的圆盘与杆做固定连接,如 图 a 所示,第二个摆的圆盘装在杆端的光滑转轴上,可相对自由转动,如图 b 所示。 图 a 的振动周期 =________;图 b 的振动周期 ________。 8、某粒子作沿 和 方向的两个谐振动的合成运动,其轨迹是限于边长为 和 的矩形 内的斜椭圆,与 轴相交于 与 两点(见图),粒子每经过 运动一周,则: (1)这两个谐振动的频率分别为_____________和_____________;振幅分别是___________

和一 (2)设沿x方向谐振动的初相位仍=0,沿》方向谐振动的初相位一 题8图 题9图 9、已知不方向的谐振动频率4=24×10 ,由图示李萨如图形可知'方向的谐振动频 率。 Hz。 10、静质量为0,长为0的均质细棒,沿棒长度方向以0.6的速度运动时,测得此棒的 长度= 一,棒的质量= 一,动量P= 一,动能2= 二、计算题
和___________; (2)设沿 方向谐振动的初相位 ,沿 方向谐振动的初相位 ________。 9、已知 方向的谐振动频率 ,由图示李萨如图形可知 方向的谐振动频 率 =_________Hz。 10、静质量为 ,长为 的均质细棒,沿棒长度方向以 0.6 的速度运动时,测得此棒的 长度 __________,棒的质量 _________,动量 ___________,动能 __________。 二、计算题

1、如图所示,A是半径为9,质量为M的细圆环,B是劲 度系数2a的轻弹性绳(其作用类似轻弹簧),C是长 为2a的轻杆,刚体可以绕Q轴在铅直平面内自由转动。现 使刚体在日=30°时静止释放(图a),刚体转动到水平位 置(图b)时,弹性绳伸长a。试计算在此位置: (1)刚体转动的角速度和角加速度: (2)刚体受到轴承的支反力。(杆和绳的质量忽略不 计)。 题1图 2、如图所示,一个高为、底盘半径为R的圆锥体,可绕其固定的铅垂轴自由旋转,转动 惯量为了,其表面上刻有一条浅槽。令锥体以角速度吗旋转,并将质量为州的小滑块由槽 的顶端静止释放,让其受重力作用下滑,(不计摩擦)。 (1)当滑块到达底边时,圆锥体的角速度是多少? (2)当滑块到达底边时,滑块沿锥体母线方向和切线方向的速度各是多少? 题2图 题3图 3、长为的轻质细杆,一端固定一质量为的小球,另一端可绕Q轴自由转动,中间与一 劲度系数为的轻弹簧相连,且细杆垂直时弹簧无伸长。若令杆自小角位移心时,静止释 放: (1)证明系统的振动为谐振动:
1、如图所示,A 是半径为 ,质量为 的细圆环,B 是劲 度系数 的轻弹性绳(其作用类似轻弹簧),C 是长 为 的轻杆,刚体可以绕 轴在铅直平面内自由转动。现 使刚体在 时静止释放(图 a),刚体转动到水平位 置(图 b)时,弹性绳伸长 。试计算在此位置: (1)刚体转动的角速度和角加速度; (2)刚体受到轴承的支反力。(杆和绳的质量忽略不 计)。 2、如图所示,一个高为 、底盘半径为 的圆锥体,可绕其固定的铅垂轴自由旋转,转动 惯量为 ,其表面上刻有一条浅槽。令锥体以角速度 旋转,并将质量为 的小滑块由槽 的顶端静止释放,让其受重力作用下滑,(不计摩擦)。 (1)当滑块到达底边时,圆锥体的角速度是多少? (2)当滑块到达底边时,滑块沿锥体母线方向和切线方向的速度各是多少? 3、长为 的轻质细杆,一端固定一质量为 的小球,另一端可绕 轴自由转动,中间与一 劲度系数为 的轻弹簧相连,且细杆垂直时弹簧无伸长。若令杆自小角位移 时,静止释 放: (1)证明系统的振动为谐振动;