
第10章气体和凝聚态 夕一、实际气体 气体模型:具有引力作用的刚性球分子的集合 1、范德瓦尔斯方 程: 1摩尔 情况下 Q+W-)=7 2、气体内 能 1摩尔情况下 8=岛+8受07-六 8=c,r-9 夕三、气体分子的威撞 1、平均碰撞频率 7=2rnd' = 1 2、平均自由程 Lond-ndkT 号三、气体运过粗 气体输运过程是指非平衡态向平衡态过渡的过程。 三种输运过程列表如下 现象 热传导 内摩擦 扩散 不均匀物理量 温度 流速 密度 微观输运量 分子的动能 分子定向运动动量 分子的质量 d为 宏观规律 =-k4T S =±nAS =-DdeAs x dx
第 10 章 气体和凝聚态 一、实际气体 气体模型:具有引力作用的刚性球分子的集合。 1、范德瓦尔斯方 程: 1 摩尔 情况下 2、气体内 能: 1 摩尔情况下 二、气体分子的碰撞 1、平均碰撞频率 , 2、平均自由程 三、气体输运过程 气体输运过程是指非平衡态向平衡态过渡的过程。 三种输运过程列表如下 现 象 热传导 内摩擦 扩散 不均匀物理量 温度 流速 密度 微观输运量 分子的动能 分子定向运动动量 分子的质量 宏观规律

系数 热传导系数 粘潘系激 书扩散系数 K= D-juz
系数 热传导系数 粘滞系数 扩散系数

第10章气体和凝聚态 号【例10-1】两个无限长圆筒共轴地套在一起,内简和外简半径分别为和心,内简和 外筒间保持恒定的温度和:,且>了。已知两简间物质的热传导系数为,试求稳定 状态时: do (1)单位时间内简放出的热量证 (2)在离轴线处(<”<8)的温度。 【解】(1)根据热传导实验定律: (1) 由稳定条件可知,两筒间任一区域温度分布都保持不变,也就是流入这区域的 热量与流出的热量必相等。取上式中△S为一圆柱面2。介于8R2之间的任 何圆柱面单位时间流过的热量均相等,即(1)式中的为常数。 (1)式可写成: dr 分离变量再积分: 【9产-「-2k7 №h是=-2xd(g-g) dt de 2eKI(T-T) dt 即: In R -In R -------- _----------- (2) (2)设在”处的温度为T,同样由热传导公式(1)可导得类似于(2)的表达 终10- 式: d坦_2xk7(T-T (3) 7=T-☒-TR-hR 由(2)、(3)式可解得: Inr-InR
第 10 章 气体和凝聚态 【例 10-1】两个无限长圆筒共轴地套在一起,内筒和外筒半径分别为 和 ,内筒和 外筒间保持恒定的温度 和 ,且 。已知两筒间物质的热传导系数为 ,试求稳定 状态时: (1)单位时间内筒放出的热量 (2)在离轴线 处( )的温度 。 【解】(1)根据热传导实验定律: (1) 由稳定条件可知,两筒间任一区域温度分布都保持不变,也就是流入这区域的 热量与流出的热量必相等。取上式中 为一圆柱面 。介于 之间的任 何圆柱面单位时间流过的热量均相等,即(1)式中的 为常数。 (1)式可写成: 分离变量再积分: 即: (2) (2)设在 处的温度为 ,同样由热传导公式(1)可导得类似于(2)的表达 式: (3) 由(2)、(3)式可解得:

号【例10-2】图中人、B为保温瓶两胆宝,两壁间抽空后存有摩尔质量为以的低压气体。 气体单位体积的质量为?。其分子自由程远大于壁间距。若内壁A的温度为1,外壁B的温 度为;子与使盖后即铁将与波童温度相当的平药能初 。试证低气压的热传导系数 k=IC, 为4p 【解】两驻间的分子分别给单位面积器壁隧撞的分子藏为 ,分子与内 的热量,所以单位时间分子给内外壁之间 传递的热量: m20 2= 式中”为单位体积中的分子数,即”M7,再注意到大=R,及 iR-c 上式可写成: 是-08-器- 1 u冬10-2 1C¥ 由此可得证低气压热传导系数: K=4证p 乡【例10-3】图为一绝热管,中间有一固定多孔嘉,其作用是允许气体缓慢通过,多孔塞 的两边各有一个绝热活塞。开始活塞A和多孔塞间装有1ol的双原子气体,活塞B紧靠多孔 嘉。在多孔塞两边保持恒定的压力差!一户,>0,气体缓慢地从左边流到右边。 (1)若是理想气体,在节流膨胀过程中,气体摘的变化多大? (2)若是实际气体,只考虑体积修正,在节流膨胀过程中,气体温度的变化多大?
【例 10-2】图中 A、B 为保温瓶两胆壁,两壁间抽空后存有摩尔质量为 M 的低压气体, 气体单位体积的质量为 。其分子自由程远大于壁间距。若内壁 A 的温度为 ,外壁 B 的温 度为 ,分子与壁碰撞后即获得与该壁温度相当的平均能量 。试证低气压的热传导系数 为 。 【解】两壁间的分子分别给单位面积器壁碰撞的分子数为 ,分子与内 外壁各碰撞一次,就输运一份 的热量,所以单位时间分子给内外壁之间 传递的热量: 式中 为单位体积中的分子数,即 ,再注意到 ,及 上式可写成: 由此可得证低气压热传导系数: 【例 10-3】图为一绝热管,中间有一固定多孔塞,其作用是允许气体缓慢通过,多孔塞 的两边各有一个绝热活塞。开始活塞 A 和多孔塞间装有 1mol 的双原子气体,活塞 B 紧靠多孔 塞。在多孔塞两边保持恒定的压力差 ,气体缓慢地从左边流到右边。 (1)若是理想气体,在节流膨胀过程中,气体熵的变化多大? (2)若是实际气体,只考虑体积修正,在节流膨胀过程中,气体温度的变化多大?

【解】(1)由热力学第一定律 Q=E,-E,+A=C(T,-T)+p,,-p =C,(T,-T)+RT-T)=(C+)T-T) 由题意在这节流膨胀过程中系统与外界绝热,所以 Q=0,得: (Cy+R)(G-T)=0 即 T2= 在此过程中,注意到系统初态终态温度不变,系统的熵 8-8=9-8+ =+ (2)根据题意,只考虑体积的修正量b,则范氏方程可写 1 成: p(V-b)=RT 或 p∥=pb+RT 再将热力学第一定律应用于该过程 2=E-E+A=CY(T-T)+pV-pV =Cy(T-T)+(p2b+RT)-(pb+RT) 1- =(Cy+R)(-)+(p2-Pi)b 由于系统与外界绝热,上式为0,即 (Cy+R)T-Ti)+(p2-P)=0 7-7i=(P-p)6-Da-p 得 Cy+R C, 题中表明乃乃>0,符 T2-T>0 即温度升高。其物理意义是本题仅考虑斥力修正量b,在 体积膨胀过程中斥力的弹性势能作正功,弹性势能减少, 而分子动能增加,因此系统经过此节流过程温度升高
【解】(1)由热力学第一定律 由题意在这节流膨胀过程中系统与外界绝热,所以 ,得: 即 在此过程中,注意到系统初态终态温度不变,系统的熵 变: (2)根据题意,只考虑体积的修正量 ,则范氏方程可写 成: 或 再将热力学第一定律应用于该过程 由于系统与外界绝热,上式为 0,即 得 题中表明 ,得 即温度升高。其物理意义是本题仅考虑斥力修正量 ,在 体积膨胀过程中斥力的弹性势能作正功,弹性势能减少, 而分子动能增加,因此系统经过此节流过程温度升高

乡【例10-4】莱空调转置,连续运转时功率为°,它吸取室内低温3处的热量向室外高 温处送去,由于室内外温装,单位时间内室外汉有热黄空三网一 传入室内。若空调 装置可看作理想卡诺机,并已知=35℃,P=200咓a=400焦耳/开秒.求稳定状 态时室内的最低温度?为多少? 【解】由卡诺机的制冷系数 说号可 可得: Qa-AT-T 稳定状态时,工、乃为常量,上式对时间求导后 T (1) 而单位时间内室外传入室内的热量 de=a(T-T) dt (2) 稳定状态时应满足 d2de 即: 或: -2+P3+=0 解此方程得: 空调机取暖时取“+”,致冷时取“一”号,代入数据 2x402x40Vm0+4x400x273+3x200 2000 1 T,=273+3约 =295.8K 即:2=228"C
【例 10-4】某空调装置,连续运转时功率为 ,它吸取室内低温 处的热量向室外高 温 处送去,由于室内外温差,单位时间内室外又有热量 传入室内。若空调 装置可看作理想卡诺机,并已知 。求稳定状 态时室内的最低温度 为多少? 【解】由卡诺机的制冷系数 可得: 稳定状态时, 、 为常量,上式对时间求导后 (1) 而单位时间内室外传入室内的热量 (2) 稳定状态时应满足 即: 或: 解此方程得: 空调机取暖时取“+”,致冷时取“—”号,代入数据: 即:

夕【例10-5】一绝热容器中间被一质量为”的绝热活塞分成容积均为0的两部分,两边 各装有温度均为0的一摩尔双原子理想气体,若将活塞向右略偏移0,然后放手,问活塞以 后如何运动?并写出其运动方程。(摩擦忽略不计) 【解】由于容器与活塞都是绝热的,左边容器1,和右 边容器2,在运动过程中都满足绝热过程方程。 p'=2' 将上式微分: 伞?+pWW=0 中=r罗 Sdx 得 由于题设最大偏移0很小,所以任意位置处1室产生 的压强改变量近似于 S 同理2室引起的压强改变量: ,=说元利奶 左右两容器内气体对活塞的合力 F=(P1-22)S=[0+A1-(P0+22)]S =248=-2p0万 根据牛顿动力学方程 41G- R= d-x dx 可得 =-20 +2p -x=0 o 考虑到理想气体状态方程 o=Vo 及双原子理想
【例 10-5】一绝热容器中间被一质量为 的绝热活塞分成容积均为 的两部分,两边 各装有温度均为 的一摩尔双原子理想气体,若将活塞向右略偏移 ,然后放手,问活塞以 后如何运动?并写出其运动方程。(摩擦忽略不计) 【解】由于容器与活塞都是绝热的,左边容器 1,和右 边容器 2,在运动过程中都满足绝热过程方程。 将上式微分: 得 由于题设最大偏移 很小,所以任意位置处 1 室产生 的压强改变量近似于 同理 2 室引起的压强改变量: 左右两容器内气体对活塞的合力 根据牛顿动力学方程 可得 即 考虑到理想气体状态方程 及双原子理想

气体的热容比”一 d'x 14 RTos2 代入上式得: 5m=0 由此得活塞的谐振动方程 4R x=x0co85洲%
气体的热容比 代入上式得: 由此得活塞的谐振动方程

第10章气体和凝聚态 10.3试计算2m范德瓦尔斯气体在下列两种过程中的内能变化: (1)体积不变,温度由21变化到22: (2)温度不变,体积由变化到。 号10.4试计算1m范德瓦尔新气体从原来体积向真空作自由影张至体积时, 其温度的变化。 号10.5阳式无战电所用真空管的真空度为13×10口,试球在27C时单位体积 中的分子数及分子平均自由程,设分子的有效直径=30×10-0m。 号108在气体收电管中,电子不新与分子相醛撞,因电子的速幸远大于分子速半, 可以认为分子近似不动。设电子的直径远小于分子的有效直径,气体分子密度为”,求电子 与气体分子碰撞的平均自由程为多少? 号1010实验测得氧气在标准状态下的扩散系数为19×10m1,试计算氧分子的 平均自由程和有效直径。 号1012图示为测定气体粘清系数”的装置,两个共轴圆筒中间充以待测气体。内筒 用金属丝沿轴悬挂,半径为R,长为L:外筒半径为R+6<R),以角速度四旋转。由 悬丝的组转测得气体对圆简的粘滑力兔为6,试证气体的钻带系数。刀2了
第 10 章 气体和凝聚态 10.3 试计算 范德瓦尔斯气体在下列两种过程中的内能变化: (1)体积不变,温度由 变化到 ; (2)温度不变,体积由 变化到 。 10.4 试计算 范德瓦尔斯气体从原来体积 向真空作自由膨胀至体积 时, 其温度的变化。 10.5 旧式无线电所用真空管的真空度为 ,试求在 时单位体积 中的分子数及分子平均自由程,设分子的有效直径 。 10.8 在气体放电管中,电子不断与分子相碰撞,因电子的速率远大于分子速率, 可以认为分子近似不动。设电子的直径远小于分子的有效直径,气体分子密度为 ,求电子 与气体分子碰撞的平均自由程为多少? 10.10 实验测得氧气在标准状态下的扩散系数为 。试计算氧分子的 平均自由程和有效直径。 10.12 图示为测定气体粘滞系数 的装置,两个共轴圆筒中间充以待测气体,内筒 用金属丝沿轴悬挂,半径为 R,长为 L;外筒半径为 ,以角速度 旋转。由 悬丝的扭转测得气体对圆筒的粘滞力矩为 G,试证气体的粘滞系数:
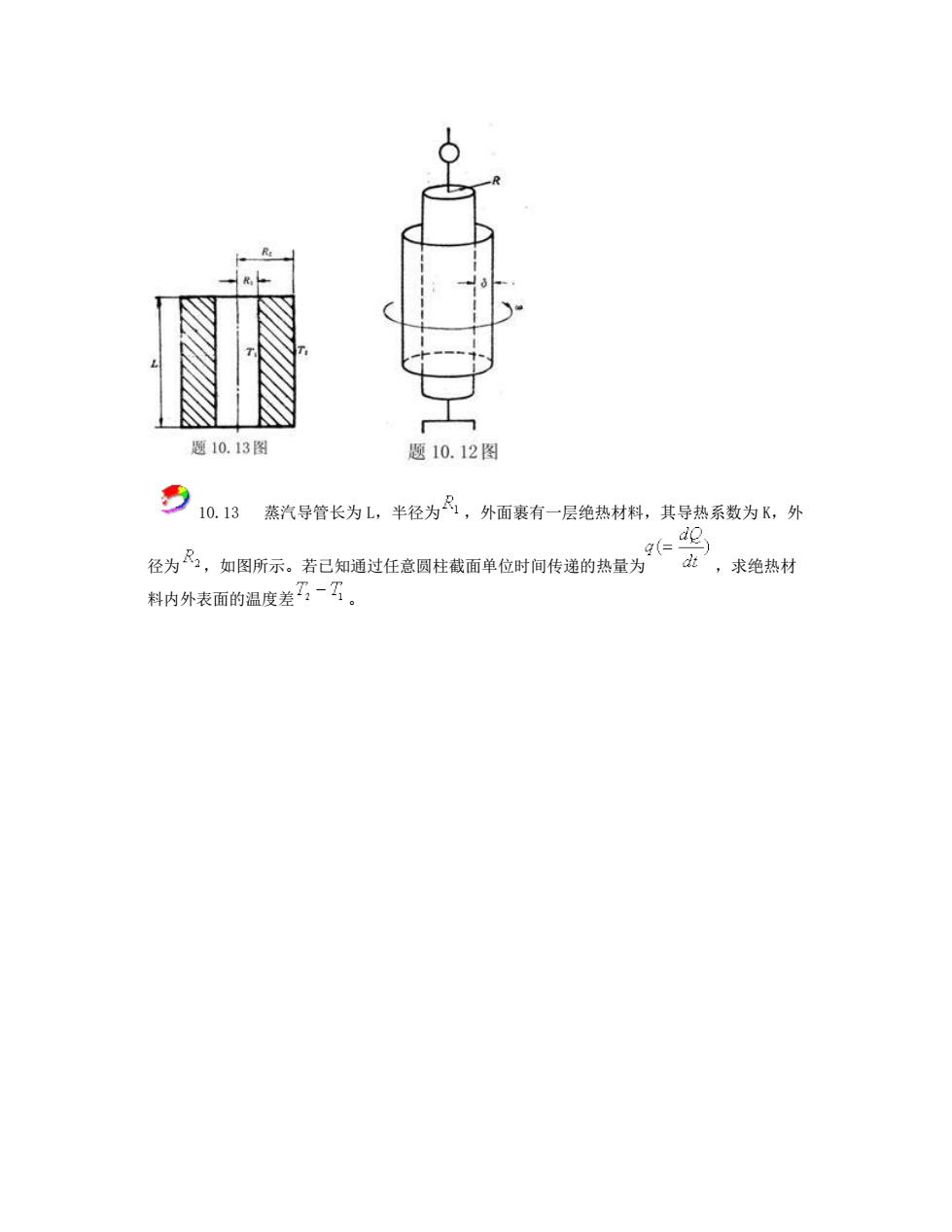
题10.13图 题10.12图 号10.13蒸汽导管长为,半径为品,外面裹有一层绝热材料,其导号热系数为。外 为民,如图所示。去已如通过任童圆柱做面单位时间传追的共量为,求轮热期 料内外表面的温度差3-了
10.13 蒸汽导管长为 L,半径为 ,外面裹有一层绝热材料,其导热系数为 K,外 径为 ,如图所示。若已知通过任意圆柱截面单位时间传递的热量为 ,求绝热材 料内外表面的温度差