
第9章热力学定律 夕一、热力学第一定律 1、热力学第一定律: 热力学第一定律是包括热现象在内的能量守恒和转换定律。它的数学表达式为: do=dE+dA (微分形式) Q=E2-8+A (积分形式) 热力学第一定律表明了:系统吸收的热量一部分使系统的内能增加,另一部分使系统对外作 功。应用热力学第一定律时必须要注意各物理量的正负号。系统吸热取“+”号,放热取 “-”号。系统对外作功取“+”号,外界对系统作功取“-”号。 2、热力学第一定律在理想气体等值过程中应用的比较表: 过 过程方程 吸收热量Q 内能增量△E 对外作功A 摩尔热容C 牌 恒量 容 等 分恒星 ,医-》仍-是G-别 M C,=+2R 压 威g-) =C,+R :恒量 RTh 或 Prr=恒量0 wT=恒量 PV-PV pr-lT-r 或 y-1 =恒量 Pr=恒量A+△E T-恒量 - B%-B严 in-YR 2-1 (3-00-1 PT- :恒量 R Cy--1
第 9 章 热力学定律 一、热力学第一定律 1、热力学第一定律: 热力学第一定律是包括热现象在内的能量守恒和转换定律。它的数学表达式为: (微分形式) (积分形式) 热力学第一定律表明了:系统吸收的热量一部分使系统的内能增加,另一部分使系统对外作 功。应用热力学第一定律时必须要注意各物理量的正负号。系统吸热取“+”号,放热取 “-”号。系统对外作功取“+”号,外界对系统作功取“-”号。 2、热力学第一定律在理想气体等值过程中应用的比较表: 过 程 过程方程 吸收热量 Q 内能增量 对外作功 A 摩尔热容 C 等 容 0 等 压 或 等 温 或 0 或 绝 热 0 或 0 多 方 或

这“比较表”的主要特点: (1)内能E是系统状态(温度)的单值函数 8=证=证C,7 内能是个状态量。内能的增量只决定于初末两个状态,与所经历的过程无关。所以表中内能 增量的表达式都是: 68=品,-岛=0,G- (2)功A是通过宏观位移来传递能量的过程量。所以表中功的表达式因过程不同而不同, 但功都可从功的定义求得,即: A=」pr (3)热量Q是通过分子间相互作用来传递能量的过程量。表中Q都可由热力学第一定律来 求得: e=岛-g+小p=c,G-+pv 或者: e-证c- 式中C为摩尔热容量。由于Q是过程量,因此式中C要与具体的过程量相对 应。 (4)摩尔热容: C,=142R 定容摩尔热容: 2 C-+2 比热容比: 1 摩尔热容C为常量的过程为多方过程。在多方过程中: -0-6 可见,当=0时为等压过程,n=l时为等温过程 当=广时为绝热过程,力→0时为等容过程 号二、循环过程
这“比较表”的主要特点: (1)内能 E 是系统状态(温度)的单值函数 内能是个状态量。内能的增量只决定于初末两个状态,与所经历的过程无关。所以表中内能 增量的表达式都是: (2)功 A 是通过宏观位移来传递能量的过程量。所以表中功的表达式因过程不同而不同, 但功都可从功的定义求得,即: (3)热量 Q 是通过分子间相互作用来传递能量的过程量。表中 Q 都可由热力学第一定律来 求得: 或者: 式中 C 为摩尔热容量。由于 Q 是过程量,因此式中 C 要与具体的过程量相对 应。 (4)摩尔热容: 定容摩尔热容: ;定压摩尔热容: ; 比热容比: 摩尔热容 C 为常量的过程为多方过程。在多方过程中: 可见,当 n=0 时为等压过程,n=1 时为等温过程 当 n= 时为绝热过程, 时为等容过程 二、循环过程

1、循环过程的特点: (1)每经历一个循环,系统内能没有改变: (②)每一循环所作的功在数值上等于P-严图封闭曲线所包围的面积。 (3)热循环的效率: 式中②1表示系统所吸收的热量,表示系统所放出的热量。 2、卡诺循环 (1)卡诺循环由两绝热过程和两等温过程组成 (2)卡诺循环的效率 n=1-9=1- (3)卡诺循环的意义 指出了所有热机的效率都小于1,提高热机效率的有效途径是提高高温热源的温度。卡诺循 环为确立热力学第二定律莫定了基础。 3、致冷循环 (1)与热机相反方向的循环为致冷循环。P-V图上逆时针循环所包围曲线的面积为外界所作 的功A。 (2)致冷系数: 号2是。 e. 对卡诺致冷机而言: w2T-可 (3)要从低温热源吸取热量向高温热源送,外界必须要消耗功为代价,对卡诺致冷机而 言,外界所需作的功: (4)供热系数: =-4+2=1+=1+w A
1、循环过程的特点: (1)每经历一个循环,系统内能没有改变; (2)每一循环所作的功在数值上等于 图封闭曲线所包围的面积。 (3)热循环的效率: 式中 表示系统所吸收的热量, 表示系统所放出的热量。 2、卡诺循环 (1)卡诺循环由两绝热过程和两等温过程组成 (2)卡诺循环的效率 (3)卡诺循环的意义 指出了所有热机的效率都小于 1,提高热机效率的有效途径是提高高温热源的温度。卡诺循 环为确立热力学第二定律奠定了基础。 3、致冷循环 (1)与热机相反方向的循环为致冷循环。P-V 图上逆时针循环所包围曲线的面积为外界所作 的功 A。 (2)致冷系数: 对卡诺致冷机而言: (3)要从低温热源吸取热量向高温热源送,外界必须要消耗功为代价,对卡诺致冷机而 言,外界所需作的功: (4)供热系数:

乡三、热力学第二定律: 1、可逆过程与不可逆过程 某一过程P中一物体从状态A变为状态B,如果我们能使状态逆向变化。从状态B回到初态 A时,周围一切也都各自回复原状。过程P就称为可逆过程。如果物体不能回复至原状态 A,或当物体回复到原状态A时而周围并不能回复原状。那么过程P称为不可逆过程。 满足机械能守恒的纯力学过程是可逆过程。 热力学过程中准静态变化过程也是可逆过程。只有理想过程才能是可逆过程。一切实际过程 都是不可逆过程。热力学中从非平衡状态到平衡态(如热传导、扩散、气体自由膨胀等)都 是不可逆过程。机械运动转化为热运动也是不可逆过程 2、卡诺定理 (1)在相同高温热源(温度为了)与相同低温热源(温度为2)之间的一切可逆机。不论 -别 用什么工作物质效率都相同。都等于 (2)在相同高温热源和相同低温热源之间工作的一切不可逆机的效率不可能高于可逆机, 3、热力学第二定律 热力学第二定律的二种说法: (1)开尔文说法:不可能制造成一种循环动作的热机,只从一个热源吸热使之完全变化为 有用的功,而其他物体不发生任何变化。 (2)克劳修斯说法:热量不能自动地从低温物体转向高温物体。 这二种说法不同,其实质是等价的。热力学第二定律表明了自然过程进行的方向和条件。用 热力学第二定律可以判别哪些过程是可以实现的,而哪些过程是不可能实现的。 4、熵和熵增加原理。 (1)克劳修斯等式:对任意可逆循环过程都有: 90 (2)熵,熵是一态函数,以符号S表示。定义为: 上式只表明了熵差,我们关心的也只是熵差(就象计算内能的改变△,力学问题中势能改
三、热力学第二定律: 1、可逆过程与不可逆过程 某一过程 P 中一物体从状态 A 变为状态 B,如果我们能使状态逆向变化。从状态 B 回到初态 A 时,周围一切也都各自回复原状。过程 P 就称为可逆过程。如果物体不能回复至原状态 A,或当物体回复到原状态 A 时而周围并不能回复原状。那么过程 P 称为不可逆过程。 满足机械能守恒的纯力学过程是可逆过程。 热力学过程中准静态变化过程也是可逆过程。只有理想过程才能是可逆过程。一切实际过程 都是不可逆过程。热力学中从非平衡状态到平衡态(如热传导、扩散、气体自由膨胀等)都 是不可逆过程。机械运动转化为热运动也是不可逆过程。 2、卡诺定理 (1)在相同高温热源(温度为 )与相同低温热源(温度为 )之间的一切可逆机。不论 用什么工作物质效率都相同。都等于 。 (2)在相同高温热源和相同低温热源之间工作的一切不可逆机的效率不可能高于可逆机, 即 。 3、热力学第二定律 热力学第二定律的二种说法: (1)开尔文说法:不可能制造成一种循环动作的热机,只从一个热源吸热使之完全变化为 有用的功,而其他物体不发生任何变化。 (2)克劳修斯说法:热量不能自动地从低温物体转向高温物体。 这二种说法不同,其实质是等价的。热力学第二定律表明了自然过程进行的方向和条件。用 热力学第二定律可以判别哪些过程是可以实现的,而哪些过程是不可能实现的。 4、熵和熵增加原理。 (1)克劳修斯等式:对任意可逆循环过程都有: (2)熵,熵是一态函数,以符号 S 表示。定义为: 上式只表明了熵差,我们关心的也只是熵差(就象计算内能的改变 ,力学问题中势能改

变一样) 熵是描述平衡态的状态函数,系统状态确立之后该系统的熵也唯一地确定下来了。因为嫡是 一个态函数。在计算两态的熵差时与过程无关。所以可以设计一个连接同样初态和终态的任 一可逆过程进行计算。 (3)理想气体的熵 引入熵概念后热力学定律方程可写成: 8,-=8+pa业 号 (4)温图 熵函数曲线下面的面积与热量相当。正循环过程中温熵图中闭合曲线的面积大小为 净吸热或为系统对外所作的净功。 (5)熵增加原理 在封闭系统中发生任何不可逆过程导致熵的增加,熵只有对可逆过程才能不变的, 这叫熵增加原理。 0 对不可逆循环有克劳修斯不等式:了 当系统和环境有能量交换时,系统从状态1到2,系统和环境(封闭系统)总的熵变: 岛9 (不可逆过程) 岛-8-9 (可逆过程) 这两式也可称作热力学第二定律的数学表达式。 熵的增加反映了能量的退化,作功机会减少。 5、热力学第二定律的统计意义:
变一样) 熵是描述平衡态的状态函数,系统状态确立之后该系统的熵也唯一地确定下来了。因为熵是 一个态函数。在计算两态的熵差时与过程无关。所以可以设计一个连接同样初态和终态的任 一可逆过程进行计算。 (3)理想气体的熵 引入熵概念后热力学定律方程可写成: (4)温熵图 熵函数曲线下面的面积与热量相当。正循环过程中温熵图中闭合曲线的面积大小为 净吸热或为系统对外所作的净功。 (5)熵增加原理 在封闭系统中发生任何不可逆过程导致熵的增加,熵只有对可逆过程才能不变的, 这叫熵增加原理。 对不可逆循环有克劳修斯不等式: 当系统和环境有能量交换时,系统从状态 1 到 2,系统和环境(封闭系统)总的熵变: (不可逆过程) (可逆过程) 这两式也可称作热力学第二定律的数学表达式。 熵的增加反映了能量的退化,作功机会减少。 5、热力学第二定律的统计意义:

一个不受外界影响的封闭系统,其内部发生的过程总是由几率小的状态向几率大的状态进 行。由包含微观状态少的宏观状态向包含微观状态多的宏观状态进行。熵和微观状态的数目 2之间的关系是: S=kin Q 式中k是玻耳兹曼常数。 夕因、三个热力学态通数的比较 态函数 温度(T) 内能(E) 熵(S) 反映系统的属性 热运动剧烈程度 热运动能量 热运动无序性 统计意义 状态量性质 内涵量 守恒量 演进量 与过程量的关系 T-T=Q/c 82-马=Q-A ≥9 相关的规律 第零定律 第一定律 第二定律
一个不受外界影响的封闭系统,其内部发生的过程总是由几率小的状态向几率大的状态进 行。由包含微观状态少的宏观状态向包含微观状态多的宏观状态进行。熵和微观状态的数目 之间的关系是: 式中 是玻耳兹曼常数。 四、三个热力学态函数的比较: 态函数 温度(T) 内能(E) 熵(S) 反映系统的属性 热运动剧烈程度 热运动能量 热运动无序性 统计意义 状态量性质 内涵量 守恒量 演进量 与过程量的关系 相关的规律 第零定律 第一定律 第二定律
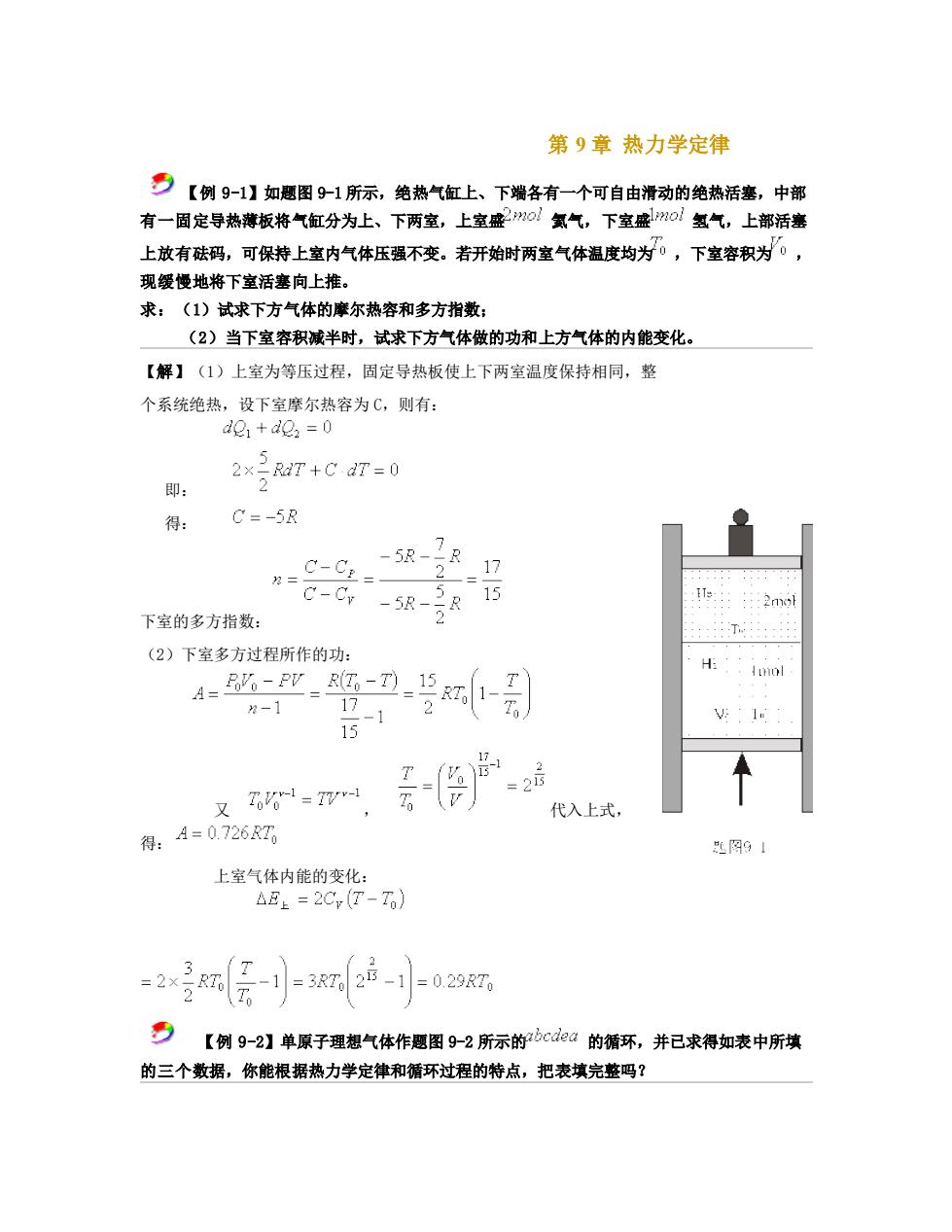
第9章热力学定律 夕【例9-1】如题图9-1所示,绝热气缸上、下端各有一个可自由滑动的绝热活塞,中部 有一固定导热薄板将气缸分为上、下两室,上室盛0氢气,下室盛0氢气,上部活塞 上放有砝码,可保持上室内气体压强不变。若开始时两室气体温度均为0,下室容积为。, 现缓慢地将下室活塞向上推。 求:(1)试求下方气体的摩尔热容和多方指数: (2)当下室容积减半时,试求下方气体做的功和上方气体的内能变化。 【解】(1)上室为等压过程,固定导热板使上下两室温度保持相同,整 个系统绝热,设下室摩尔热容为C,则有 de+de2=0 2×R7+Cd7=0 即: 得: C=-5R C-C= 17 下室的多方指数: C-Gr -5R-38 15 (2)下室多方过程所作的功: H 4”-0号别 -1 -121 1 15 又061-y-1 -2 代入上式, 得:A=0726R7 些网91 上室气体内能的变化: △E上=2Cr(T-To) 号【例9-2】单原子理想气体作愿图9-2所示的如d0的循环,并已求得如表中所填 的三个数据,你能根据热力学定律和循环过程的特点,把表填完整吗?
第 9 章 热力学定律 【例 9-1】如题图 9-1 所示,绝热气缸上、下端各有一个可自由滑动的绝热活塞,中部 有一固定导热薄板将气缸分为上、下两室,上室盛 氦气,下室盛 氢气,上部活塞 上放有砝码,可保持上室内气体压强不变。若开始时两室气体温度均为 ,下室容积为 , 现缓慢地将下室活塞向上推。 求:(1)试求下方气体的摩尔热容和多方指数; (2)当下室容积减半时,试求下方气体做的功和上方气体的内能变化。 【解】(1)上室为等压过程,固定导热板使上下两室温度保持相同,整 个系统绝热,设下室摩尔热容为 C,则有: 即: 得: 下室的多方指数: (2)下室多方过程所作的功: 又 , 代入上式, 得: 上室气体内能的变化: 【例 9-2】单原子理想气体作题图 9-2 所示的 的循环,并已求得如表中所填 的三个数据,你能根据热力学定律和循环过程的特点,把表填完整吗?

过程 日一b等压 250焦耳 b一c绝热 75焦耳 一d等容 d一a等温 125焦耳 循环效率7三 塑32 【解】a一b等压过程 e-c-0-g-刀 -Pe-0=4 焦耳 由热力学第一定律 8,-B。=0-A=250-100=150焦耳 b一c绝热过程中 Q=0,B。-E,=-A=-75焦耳 d一a等温过程中 品-日4=0,2=-125焦耳 对整个循环过程 68=0,可得8:-8=-75焦耳 c一d等容过程中 4=0,0=风-8.=-75焦耳 整个循环的功 工4A=100+750+0-125=50焦耳 由此得循环效率 7=501250=20% 最后请看填好后的表 过程 AB a-b等压 250焦耳 100 150
过程 Q A a—b 等压 250 焦耳 b—c 绝热 75 焦耳 c—d 等容 d—a 等温 -125 焦耳 循环效率 【解】a—b 等压过程 得: 焦耳 由热力学第一定律 焦耳 b—c 绝热过程中 , 焦耳 d—a 等温过程中 , 焦耳 对整个循环过程 ,可得 焦耳 c—d 等容过程中 , 焦耳 整个循环的功 焦耳 由此得循环效率 最后请看填好后的表 过程 Q A a—b 等压 250 焦耳 100 150

b一c绝热 0 75焦耳 75 一d等容 -75 75 d一a等温 125 -125焦耳 0 循环效率 7=209% 乡【例9-3】单原子理想气体作如题图9-3的循环,试求该循环的热机效率。(取1大 气压升≈100焦耳) 293 些度9补 【解】这三角形bc循环过程作的净功为这三角形所包围的面积 4=AP△r=28-20-) -1x110=50 (1) 在循环过程中bc为放热过程,本题中不必计算:ca为等容吸热过程。它吸热 0.c,区-0-7-功-g-助 -22x1-1xDx10/=150 对于ab这过程并不是净吸热,首先要判别这过程中从吸热转化为放热的位置©。参阅图9 弘。由热力学第一定律的微分形式: 0=B+nr-证C7+na =27+p=0+Ra
b—c 绝热 0 75 焦耳 -75 c—d 等容 -75 0 -75 d—a 等温 -125 -125 焦耳 0 循环效率 【例 9-3】单原子理想气体作如题图 9-3a 的循环,试求该循环的热机效率。(取 1 大 气压升 100 焦耳) 【解】这三角形 abc 循环过程作的净功为这三角形所包围的面积。 (1) 在循环过程中 bc 为放热过程,本题中不必计算;ca 为等容吸热过程。它吸热 对于 ab 这过程并不是净吸热,首先要判别这过程中从吸热转化为放热的位置 e。参阅图 9- 3b。由热力学第一定律的微分形式:

d№-0 a到b过程中由吸热转化为放热位置e的条件为dW ,由上式得: 器-+p+多-=0 i+2P P 即:D (2) 这说明ab过程中的e点处恰与一绝热线相切。ab直线过程方程满足: 3+31 或P+∥=3 (3) 由直线方程可得 dv (4) 又单原子理相气体的入2,解2)@)纱t相e的伦面 - 系统从a到e的过程中吸收热量Q。:可由热力学第一定律来求: Qor=E,-Ea +Au 式中 3m R(T,-T) 品-品心-0- 2×15-2×0×100 =g-)=6×8 -16.4J 在ae过程中所作的功,可用ae过程方程下方的梯形面积来计算: -8+RXg-)-e+号号-0x10w =136.71 得ae过程中吸热 0=E。-g。+A=16.4+136.7=1531W 循环过程所吸热 Q1=2a+Q=150+1531=3037 由此得循环效率 7=
a 到 b 过程中由吸热转化为放热位置 e 的条件为 ,由上式得: 即: (2) 这说明 ab 过程中的 e 点处恰与一绝热线相切。ab 直线过程方程满足: 或 (3) 由直线方程可得 (4) 又单原子理想气体的 代入(2),解(2)(3)(4)式得 e 的位置 系统从 a 到 e 的过程中吸收热量 可由热力学第一定律来求: 式中 在 ae 过程中所作的功,可用 ae 过程方程下方的梯形面积来计算: 得 ae 过程中吸热 循环过程所吸热 由此得循环效率