
第5章刚体力学基础 夕一、刚体定轴转动的运动学措述 da d2e 角位移△日,角速度“二论,角加速度”水之 在匀变速转动条件下,即角加速度:为常数时有: =a+d让 m2-m,2=2a日 角速度是矢量,在定轴转动中其方向沿着轴向,它与刚体中r处点的线速度的矢量关系: 疗=面x产 角速度是矢量,在定轴转动中其方向沿着轴向,它与刚体中r处点的线加速度关系 京=立x疗+西x(击×) 其中:云=立×产为切向加速度:司,=①×(@×刀为法向加速度。 夕二、转动定律 1、力矩证=F×京 力矩一般说来是一空间矢量,在定轴转动中,角速度方向已经确定,沿转动轴方向,刚体转 动状态的改变只与力矩在这一方向上的分量有关。在定轴转动中,力矩可简化为代数量 其量值:M=PnP 2、转动惯量J 转动惯量是表示物体转动惯性的物理量,它与物体的质量大小、质量的分布及转轴位置都有 关系,是转动问题中的一个重要的物理量: (1)定义式: 不连续分布的质点系: 1=∑m52 J=r'dm 质量连续分布的物体 (2)平行轴定理: 任意物体绕某固定轴0的转动惯量为,绕通过质心C而平行于固定轴0的转动惯量为 了。,0轴与C轴间距为d,转动物体的总质量为,那么:了=。+md (3)垂直轴定理: 在少平面上,有一薄形板,薄板饶不轴的转动惯量为·,薄板饶》轴的转动惯量 为,那么,薄板饶通过轴的交点0垂直于平面的2轴的转动惯量
第 5 章 刚体力学基础 一、刚体定轴转动的运动学描述 角位移 ,角速度 ,角加速度 在匀变速转动条件下,即角加速度 为常数时有: ; ; 角速度是矢量,在定轴转动中其方向沿着轴向,它与刚体中 r 处点的线速度的矢量关系: 角速度是矢量,在定轴转动中其方向沿着轴向,它与刚体中 r 处点的线加速度关系: 其中: 为切向加速度: 为法向加速度。 二、转动定律 1、力矩 力矩一般说来是一空间矢量,在定轴转动中,角速度方向已经确定,沿转动轴方向,刚体转 动状态的改变只与力矩在这一方向上的分量有关。在定轴转动中,力矩可简化为代数量。 其量值: 2、转动惯量 J 转动惯量是表示物体转动惯性的物理量,它与物体的质量大小、质量的分布及转轴位置都有 关系,是转动问题中的一个重要的物理量: (1)定义式: 不连续分布的质点系: 质量连续分布的物体: (2)平行轴定理: 任意物体绕某固定轴 O 的转动惯量为 ,绕通过质心 C 而平行于固定轴 O 的转动惯量为 ,O 轴与 C 轴间距为 d,转动物体的总质量为 m,那么: (3)垂直轴定理: 在 平面上,有一薄形板,薄板饶 轴的转动惯量为 ,薄板饶 轴的转动惯量 为 ,那么,薄板饶通过 轴的交点 O 垂直于 平面的 轴的转动惯量:

J:=J,+J, 转动惯量除上述的计算方法,对于匀质简单形状的几何体可查表查得它的转动惯量,对于非 匀质或不规则的物体我们可以经过实验方法来测定: 3、转动定律: 一般形式为: 在刚体定轴转动中: 转动定律是转动问题中的基本规律,它的地位与质点动力学牛顿第二定律相当。用转动定律 的解题步骤也与牛顿第二定律类同。仍为分析研究对象,画出隔离体受力图,选取合适坐 标,列出相应方程,和求解讨论。因注意到过、了、a相对同一轴而言,M=a是个代 数式。 夕三、角动量原理 1、刚体定轴转动角动量: 2、角动量原理: 「M出=i-i 一般形式: 刚体定轴转动: ∫M业=忘-J.应 3、角动量守恒定律 系统(质点系或物体组)受到的合外矩为零,则系统的角动量守恒 M=0 ∑乙,=恒矢量 物体组绕z轴做定轴转动时: M=0 J应=恒量 应用角动量守恒定律时应注意: (1)合外力矩为零的条件而不是合外力为零的条件 (2)适用于惯性参照系(或质心参照系),对同一转轴而言 (3)适用于刚体也适用于非刚体 (4)适用于宏观也适用于微观 日、转动中的功能关系
。 转动惯量除上述的计算方法,对于匀质简单形状的几何体可查表查得它的转动惯量,对于非 匀质或不规则的物体我们可以经过实验方法来测定。 3、转动定律: 一般形式为: 在刚体定轴转动中: 转动定律是转动问题中的基本规律,它的地位与质点动力学牛顿第二定律相当。用转动定律 的解题步骤也与牛顿第二定律类同。仍为分析研究对象,画出隔离体受力图,选取合适坐 标,列出相应方程,和求解讨论。因注意到 、 、 相对同一轴而言, 是个代 数式。 三、角动量原理 1、刚体定轴转动角动量: 2、角动量原理: 一般形式: 刚体定轴转动: 3、角动量守恒定律: 系统(质点系或物体组)受到的合外矩为零,则系统的角动量守恒。 恒矢量 物体组绕 z 轴做定轴转动时: 恒量 应用角动量守恒定律时应注意: (1)合外力矩为零的条件而不是合外力为零的条件 (2)适用于惯性参照系(或质心参照系),对同一转轴而言 (3)适用于刚体也适用于非刚体 (4)适用于宏观也适用于微观 四、转动中的功能关系

1、力矩的功: A=「Mde 2、刚体的转动动能: =2m 3、功能定理:A=-0 式中A是指内力、外力、内力矩、外力矩的总功,而动能巴和巴知是质心的平动动能与刚 体或非刚体绕质心转动动能的总和。 4、机械能守恒 非保守内力、内力矩、非保守外力和外力矩不作功时系统的总机能保持不变。 号五、刚体的平面运动 刚体中某一平面,被限制在一固定平面内运动,有三个自由度,处理刚体平面运动有如下的 方法: 方法一,刚体平面运动可以分解为以质心运动为代表的平动和绕过质心的垂直轴的转动 质心运动服从质心运动规律】 ∑R,=9ag ∑F,=ma 绕质心轴转动服从质心系转动定律和动能定理 M=Ja 方法二,刚体平面运动可视为饶瞬时转轴P作纯转动。 对瞬轴的动能定理 式中,=J。+w2 但对瞬轴的转动定律,只有在,=J,+m“是个常数的条件下才能成立,例如圆柱体和球 作纯滚动时,,1=0,则对瞬时轴的转动定律才成立。 M,=J,a 六、刚体的进动
1、力矩的功: 2、刚体的转动动能: 3、功能定理: 式中 是指内力、外力、内力矩、外力矩的总功,而动能 和 是质心的平动动能与刚 体或非刚体绕质心转动动能的总和。 4、机械能守恒 非保守内力、内力矩、非保守外力和外力矩不作功时系统的总机能保持不变。 恒量 五、刚体的平面运动 刚体中某一平面,被限制在一固定平面内运动,有三个自由度,处理刚体平面运动有如下的 方法: 方法一,刚体平面运动可以分解为以质心运动为代表的平动和绕过质心的垂直轴的转动。 质心运动服从质心运动规律。 绕质心轴转动服从质心系转动定律和动能定理 方法二,刚体平面运动可视为饶瞬时转轴 P 作纯转动。 对瞬轴的动能定理 ; 式中 但对瞬轴的转动定律,只有在 是个常数的条件下才能成立,例如圆柱体和球 作纯滚动时, ,则对瞬时轴的转动定律才成立。 六、刚体的进动

进动是刚体的一种非定点运动,绕自转轴转动的回转仪在重力矩作用下,非但不会倾倒:而 且自转轴还会旋转。 1、回转仪进动的物理实质(在转动参照系中观察) 重力矩作用使回转仪倾倒:回转仪倾倒而产生垂直于自转轴的惯性力矩,使回转仪进动:回 转仪进动又产生与重力矩平衡的惯性力矩,使回转仪不再领倒,继续进动 2、回转仪进动方向的规则 回转仪的进动使其自转角速度的指向,具有向外加力矩指向靠拢的趋势。 =QxE dt 3、回转仪进动角速度: Q.-Jo Ja 对于给定刚体,进动角速度的大小,与外加力矩成正比,与刚体自转角速度成反比
进动是刚体的一种非定点运动,绕自转轴转动的回转仪在重力矩作用下,非但不会倾倒;而 且自转轴还会旋转。 1、回转仪进动的物理实质(在转动参照系中观察) 重力矩作用使回转仪倾倒;回转仪倾倒而产生垂直于自转轴的惯性力矩,使回转仪进动;回 转仪进动又产生与重力矩平衡的惯性力矩,使回转仪不再倾倒,继续进动。 2、回转仪进动方向的规则 回转仪的进动使其自转角速度的指向,具有向外加力矩指向靠拢的趋势。 3、回转仪进动角速度: 对于给定刚体,进动角速度的大小,与外加力矩成正比,与刚体自转角速度成反比

第5章刚体力学基础 夕【例5-1】计算质量为”半径为8的均质球体绕其轴线的转动惯量。 【解】方法一,由转动惯量的定义,由积分法求解,如图所示,体 密度为P的球体中一薄片圆盘的转动惯量 a-n=pg证 -po'de-DrR'cosR0 ↑y 号am0-meda-R 方法二,利用对称性求解 J,=[(y2+z2)dm J,-[(z2+x2)am J:=[(x2+y2)dm 由对称 .=,=以.=.+,+0=e+y+2n @图5-1 性 -ro4一0号 =2pRR”=亏mR 号【例5-2】设电风扁的功率恒定不变为P,风叶受到的空气阻力施与风叶旋转的角速度 四成正比,比例系数的k,并已知风叶转子的总转动惯量为J。 (1)原来静止的电扇通电层秒时刻的角速度。 (2)电扇稳定转动时的转速为多大? (3)电扇以稳定转速旋转时,断开电源后风叶还能继线转多少角度? M= 【解】1)电风扇的功率P=@,电动力矩“西,而阻力矩,=一@,由此对风扇 列特动定律方品,名和=如
第 5 章 刚体力学基础 【例 5-1】计算质量为 半径为 的均质球体绕其轴线的转动惯量。 【解】方法一,由转动惯量的定义,由积分法求解,如图所示,体 密度为 的球体中一薄片圆盘的转动惯量 方法二,利用对称性求解 由对称 性 【例 5-2】设电风扇的功率恒定不变为 P,风叶受到的空气阻力矩与风叶旋转的角速度 成正比,比例系数的 k,并已知风叶转子的总转动惯量为 J。 (1)原来静止的电扇通电后 秒时刻的角速度。 (2)电扇稳定转动时的转速为多大? (3)电扇以稳定转速旋转时,断开电源后风叶还能继续转多少角度? 【解】(1)电风扇的功率 ,电动力矩 ,而阻力矩 ,由此对风扇 列出转动定律方程:

jda=d 卫-四 将此微分方程分离变量: 1d(p-ka 可化成:日 p-Ka 得: (2)当:→60时,可得凤叶稳定时的转速。 或者直接从转动定律来求,因为稳定时电动转矩和与阻力矩平衡,角加速度为零, 2-km.=0 (3)电扇断开电源后,只受到空气阻力矩作用,它的转动微分方程: 分衣.治户 得:=m,e 转过的角度: 风叶转过的角度也可从功能关系求解: M,de=d讴, -ka d0=dla'-Jara 即: 2 -(kde=[Jda 号【例5-3】如图品所示,半轻分别是和:、转动惯量分别是1和?的两个圆柱 体,可绕垂直于图面的轴转动,最初大圆柱体的角速度为,现在将小图柱体向左靠近,直 到它碰到大圆柱体为止。由于相互间的摩擦力,小圆柱体被带着转动,最后,当相对滑动停 止时,两圆柱体各以恒定角速度沿相反方向转动。 试问这种情况角动量是否守恒?为什么?小圆柱的最终角速度多大?
将此微分方程分离变量: 可化成: 得: (2)当 时,可得风叶稳定时的转速。 或者直接从转动定律来求,因为稳定时电动转矩和与阻力矩平衡,角加速度为零, 即: ,得 。 (3)电扇断开电源后,只受到空气阻力矩作用,它的转动微分方程: 分离变量后积分: 得: 转过的角度: 风叶转过的角度也可从功能关系求解: 即: 【例 5-3】如图 a 所示,半径分别是 和 、转动惯量分别是 和 的两个圆柱 体,可绕垂直于图面的轴转动,最初大圆柱体的角速度为 ,现在将小圆柱体向左靠近,直 到它碰到大圆柱体为止。由于相互间的摩擦力,小圆柱体被带着转动,最后,当相对滑动停 止时,两圆柱体各以恒定角速度沿相反方向转动。 试问这种情况角动量是否守恒?为什么?小圆柱的最终角速度多大?

题图5-3a 项图5-3h 【解】大、小两圆柱体组成的系统受到的一对摩擦力和一对正压力不改变系统的角动量。但 0O轴对系统有外力作用。如图b所示,01轴对大圆柱体的作用力只不通过:轴,对 轴形成外力矩:O轴对小圆柱体的作用力不通过O轴,对O轴形成外力矩。定轴转动公 式中各与轴有关的量,例如力矩、角动量等均对同一轴而言。现不管相对轴,还是相对 轴,都存在外力矩,系统角动量均不守恒。所以,此种啮合方式只能分别对1轴和?轴运用 角动量定理。设垂直于纸面向里为正向: 对9轴 -R=J1画1-J 对0轴 -R,=-J. 无相对滑动 Ra凸=R2a J1R1R200 解得 转向如图所示。 夕【例5-4】以速度作匀速运动的汽车上,有一质量为”(“较小),边长为的立 方形货物箱,如图所示。当汽车遇到前方障碍物急刹车停止时,货物箱绕其底面A边翻转。 试求: (1)汽车刹车停止瞬时,货物箱翻转的角速度及角加速度: (2)此时,货物箱A边所受的支反力。 7777 题图5-48 题图5-46 【解】汽车突然刹车并立即停止,由于惯性的作用,货物箱必绕A轴转动,亦即货物箱的运动
【解】大、小两圆柱体组成的系统受到的一对摩擦力和一对正压力不改变系统的角动量。但 轴对系统有外力作用。如图 b 所示, 轴对大圆柱体的作用力 不通过 轴,对 轴形成外力矩; 轴对小圆柱体的作用力 不通过 轴,对 轴形成外力矩。定轴转动公 式中各与轴有关的量,例如力矩、角动量等均对同一轴而言。现不管相对 轴,还是相对 轴,都存在外力矩,系统角动量均不守恒。所以,此种啮合方式只能分别对 轴和 轴运用 角动量定理。设垂直于纸面向里为正向: 对 轴 。 对 轴 。 无相对滑动 。 解得 , 转向如图所示。 【例 5-4】以速度 作匀速运动的汽车上,有一质量为 ( 较小),边长为 的立 方形货物箱,如图所示。当汽车遇到前方障碍物急刹车停止时,货物箱绕其底面 A 边翻转。 试求: (1)汽车刹车停止瞬时,货物箱翻转的角速度及角加速度; (2)此时,货物箱 A 边所受的支反力。 【解】汽车突然刹车并立即停止,由于惯性的作用,货物箱必绕 A 轴转动,亦即货物箱的运动

在瞬间由平动变为转动。此瞬间货物箱受到的重力和地面支承力对A轴的冲量矩可忽略不计, 货物箱对A轴角动量守恒。 m场2J@ 等式左项为刹车前瞬时货物箱对A轴的平动角动量。右项中对A轴的转动惯量,据平行轴定理 有 2 3 Uo 解得货物箱翻转的角速度: 24。 货物箱翻转瞬时,只受重力矩作用,根据转动定律: 求得角加速度: =器 汽车停止瞬时,货物箱以四绕A轴转动,其质心C的加速度沿切向、法向的分量为: 321, a.=2=32 2 8 根据质心运动定理,取如图b坐标,有: N.=ma =ma cos45-ma cos45 N.-mg=ma =-ma cos45-ma cos 45 解得货物箱A边受到的支反力: 号【例5-5】如图所示,一半经为、质量为的均质圈盘在水平面内绕通过圆心且垂 直于盘面的垂直轴转动。现加一轴向的恒力矩以,使盘从静止开始加速转动。若从运动一开 222 始,的满以一在的质量境加家均匀诡将砂子落在金上离装做处,当秒子落下的质量的好 等于圆盘质量”0时,圆盘的角速度为多大?
在瞬间由平动变为转动。此瞬间货物箱受到的重力和地面支承力对 A 轴的冲量矩可忽略不计, 货物箱对 A 轴角动量守恒。 , 等式左项为刹车前瞬时货物箱对 A 轴的平动角动量。右项中对 A 轴的转动惯量,据平行轴定理 有 解得货物箱翻转的角速度: 。 货物箱翻转瞬时,只受重力矩作用,根据转动定律: 求得角加速度: 汽车停止瞬时,货物箱以 绕 A 轴转动,其质心 C 的加速度沿切向、法向的分量为: , 。 根据质心运动定理,取如图 b 坐标,有: 解得货物箱 A 边受到的支反力: , 。 【例 5-5】如图所示,一半径为 、质量为 的均质圆盘在水平面内绕通过圆心且垂 直于盘面的垂直轴转动。现加一轴向的恒力矩 ,使盘从静止开始加速转动。若从运动一开 始,砂漏以 的质量增加率均匀地将砂子落在盘上离轴线 处,当砂子落下的质量恰好 等于圆盘质量 时,圆盘的角速度为多大?

【解】方法一,用质量流动,反冲力矩及转动定律来解: 反冲力 留9=网 反冲力矩 fr=-arg r=-ar'g 转动定律 M-m=%+g内0 对上式分离变量并积分 d2 M-ar'g 1 ar'gmr 1 M 3%2 1-a'ng 3% M %R2+9.r 1 题图5-5 2M 四= 注意到式中=,可解得: g(R2+2r2) 方法二,对沙子和圆盘组成的系统,应用角动量原理: M=Jm-Jo吗 注意到式中 9,=0 得 8=吃mR+m@ 同样得上述结果, 夕【例5-6】一均质细棒的质量为4,长为,开始时处于水平方位,静止于支点0 上。一睡子沿竖直方向在X=处撞击细棒,给棒的冲量为,。试讨论细棒被球撞击后的运 动情况
【解】方法一,用质量流动,反冲力矩及转动定律来解: 反冲力 反冲力矩 转动定律 对上式分离变量并积分 注意到式中 ,可解得: 。 方法二,对沙子和圆盘组成的系统,应用角动量原理: 注意到式中 , 得: 同样得上述结果。 【例 5-6】一均质细棒的质量为 ,长为 ,开始时处于水平方位,静止于支点 O 上。一锤子沿竖直方向在 处撞击细棒,给棒的冲量为 。试讨论细棒被球撞击后的运 动情况
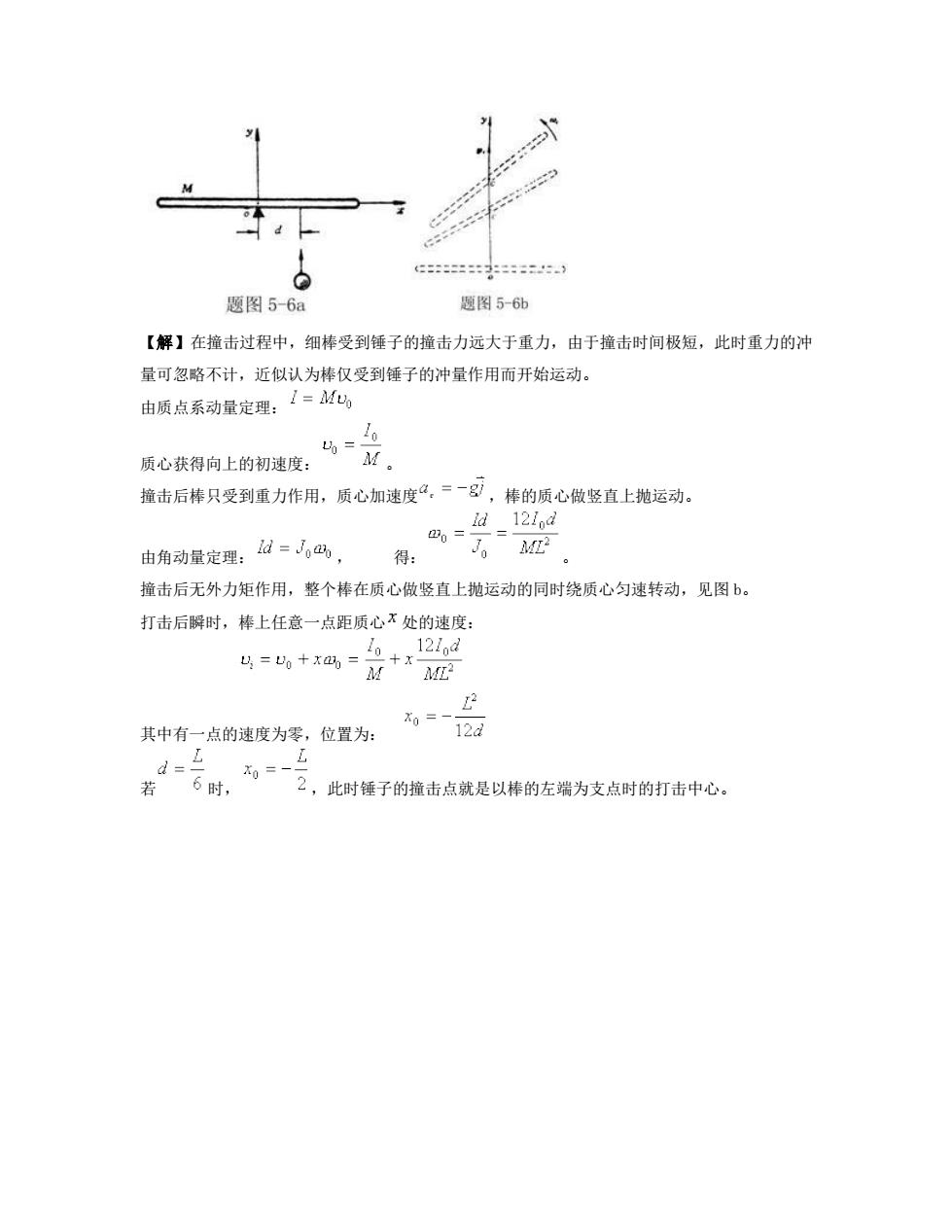
之 553255 题图5-6a 题图5-6b 【解】在撞击过程中,细棒受到锤子的撞击力远大于重力,由于撞击时间极短,此时重力的冲 量可忽略不计,近似认为棒仅受到锤子的冲量作用而开始运动。 由质点系动量定理:=M 质心获得向上的初速度: 撞击后棒只受到重力作用,质心加速度只.=一87,棒的质心做竖直上抛运动。 ,d_121od 由角动量定理:=, 得 撞击后无外力矩作用,整个棒在质心做竖直上抛运动的同时绕质心匀速转动,见图b。 打击后瞬时,棒上任意一点距质心不处的速度: 4=,+x画=证 2 其中有一点的速度为零,位置为: =12d ,与=一左,比时隆子的童击点就是以样的左流为支点时的打击中心
【解】在撞击过程中,细棒受到锤子的撞击力远大于重力,由于撞击时间极短,此时重力的冲 量可忽略不计,近似认为棒仅受到锤子的冲量作用而开始运动。 由质点系动量定理: 质心获得向上的初速度: 。 撞击后棒只受到重力作用,质心加速度 ,棒的质心做竖直上抛运动。 由角动量定理: , 得: 。 撞击后无外力矩作用,整个棒在质心做竖直上抛运动的同时绕质心匀速转动,见图 b。 打击后瞬时,棒上任意一点距质心 处的速度: 其中有一点的速度为零,位置为: 若 时, ,此时锤子的撞击点就是以棒的左端为支点时的打击中心