
第13章电介质 夕一、电极化强度 1、电极化强度是描述电介质极化强弱程度的物理量,定义单位为体积内分子电偶极矩的矢 量和,即: 2、电极化规律,电极化强度P与介质中的电场强度成正比,比例系数之:叫电极化率,各项 同性时户=无.6豆=(G-18豆 3、极化强度P与极化电荷面密度口的关系 g=P.=P=Pcos日 式中日为极化强度P与介质表面外法线方向的夹角。 两介质界面0=(月-)。 夕二、电介质中的高斯定理电位移矢量 1、高斯定理在有介质条件下的应用。 由真空中的高斯定理,在介质中考虑到极化电荷?的影响 f2a,+90 又 g'=手ps f(E+P5=∑g0 2、电位移矢量D 定义:0=+ 3、介质中的高斯定理 fDs=∑g0 引进电位移矢量D之后使介质中的高斯定理形式简化,闭合曲面的电位移通量只和自由电荷 9·有关,而与电介质的极化电荷无关。应注意极化电荷9(或极化强度户)的作用隐含在 电位移矢量D中,所以电位移矢量D既描述了介质中的场强E也描述了介质的极化。 4、各向同性均匀电介质充满电场所在空间,或各向同性均匀电介质的表面是等势面时,参 量D,豆,户等之间的相互关系。 由定义式 D=应+ 0-60+08-多 P=Xe6园 可得:
第 13 章 电介质 一、电极化强度 1、电极化强度是描述电介质极化强弱程度的物理量,定义单位为体积内分子电偶极矩的矢 量和,即: 。 2、电极化规律,电极化强度 与介质中的电场强度成正比,比例系数 叫电极化率,各项 同性时 3、极化强度 与极化电荷面密度 的关系 式中 为极化强度 与介质表面外法线方向的夹角。 两介质界面 二、电介质中的高斯定理 电位移矢量 1、高斯定理 在有介质条件下的应用。 由真空中的高斯定理,在介质中考虑到极化电荷 的影响 又 得 2、电位移矢量 定义: 3、介质中的高斯定理 引进电位移矢量 之后使介质中的高斯定理形式简化,闭合曲面的电位移通量只和自由电荷 有关,而与电介质的极化电荷无关。应注意极化电荷 (或极化强度 )的作用隐含在 电位移矢量 中,所以电位移矢量 既描述了介质中的场强 也描述了介质的极化。 4、各向同性均匀电介质充满电场所在空间,或各向同性均匀电介质的表面是等势面时,参 量 , , 等之间的相互关系。 由定义式 及 可得:

8=68, 8,=1+x ii 在上述条件下并且有 j=2= 京、夏 5、介质的击穿 在很强的电场作用下介质的绝缘性能会遭到破坏,这称为介质的击穿。某种介质能承受的最 大电场强度叫做击穿场强。 号三、电多的边值关系(在边界面上无自由电青的条件 1、电介质分界面两边电位移的法向分量相等,即 Du=Dis 2、电介质分解面两边电场强度的切向分量相等,即品:=B, g8-三= 3、电位移线的折射定律 g8, 夕四、电场的能量 1、点电荷的能量 1÷日g9, 或 或 ”号 2、电荷连续分布时的电能 对体电荷分布 理=n 对面电荷分布 W-[ais 3、电场的能量 W= 电场的能量密度 2s 五、各向同性介质中静电场量基本关系
在上述条件下并且有 5、介质的击穿 在很强的电场作用下介质的绝缘性能会遭到破坏,这称为介质的击穿。某种介质能承受的最 大电场强度叫做击穿场强。 三、电场的边值关系(在边界面上无自由电荷的条件下) 1、电介质分界面两边电位移的法向分量相等,即 2、电介质分解面两边电场强度的切向分量相等,即 3、电位移线的折射定律 四、电场的能量 1、点电荷的能量 或 或 2、电荷连续分布时的电能 对体电荷分布 对面电荷分布 3、电场的能量 电场的能量密度 五、各向同性介质中静电场量基本关系
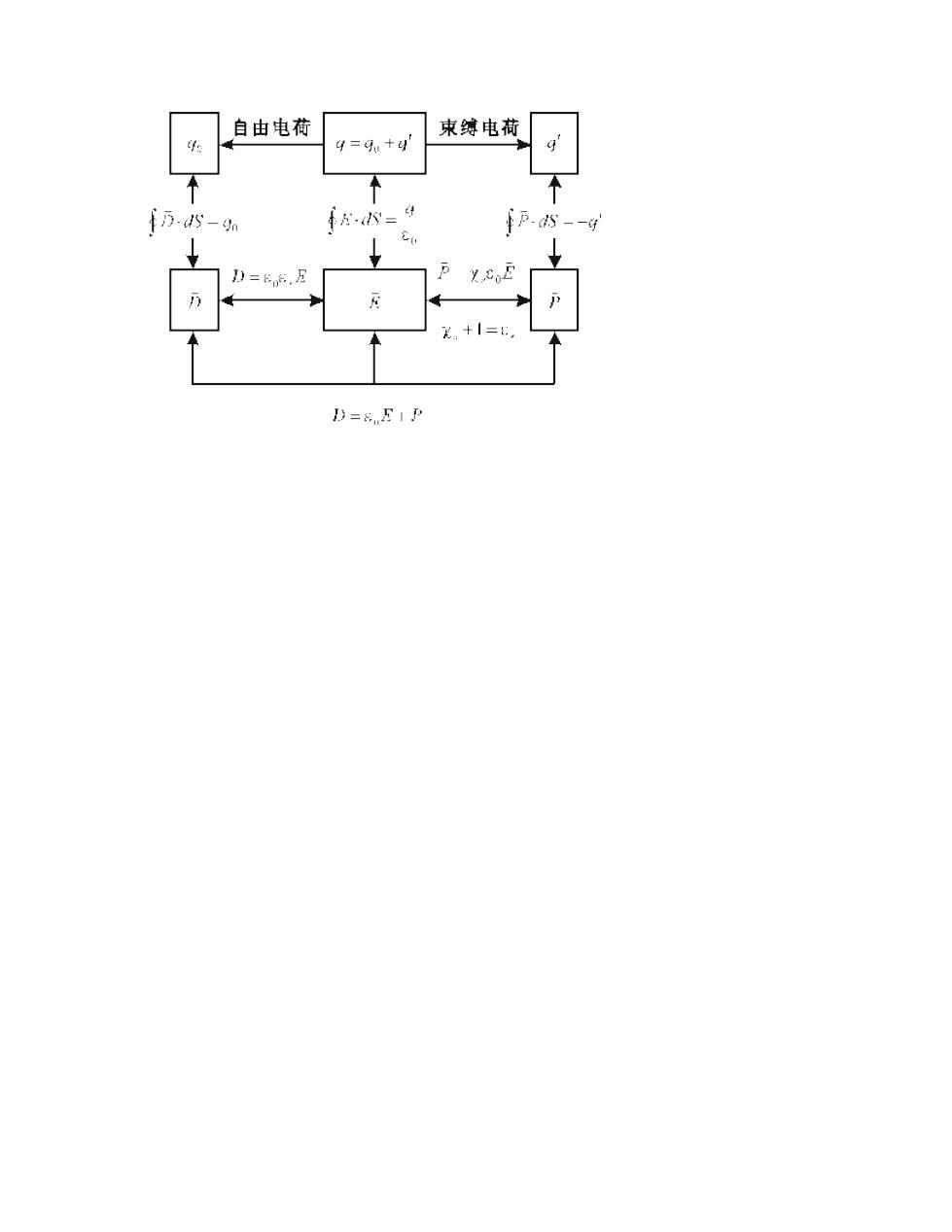
自由电荷 9=+g 束绮电荷 万- 千N= 4 .--g X.+1= D=8 EIP

第13章电介质 5 【例13-1】如题图13-1a所示平行板电容器,两板间距为。将它充电至电势差 为心,然后断开电源,插入2的相对介电常数为的电介质平板 (1)求电介质中的D,豆,户的大小及电介质表面的极化电荷'。 (2)求电容器两板板间的电势差; (3)画出电容器内的D线、豆线及P线: (4)如果在插入2电介质平板后,保持电源接通。那么电介质中的、豆、户又为多大? 西图131 【解】(1)插入电介质平板之前,电容器极板间的场强 8,因此 ⊙0三气d。虽然插入介质。由于已断开电源所以 豆、立,由介质中高斯定理可知 。=马豆不夜,由此我们可计续, D=00-60d 8=D 0_10 p=56-6-0g-54智 s.d Ey gB=g-1。 两d 插入介质板后两平行板间的电势差 8号号+是兰若
第 13 章 电介质 【例 13-1】如题图 13-1a 所示平行板电容器,两板间距为 。将它充电至电势差 为 ,然后断开电源,插入 的相对介电常数为 的电介质平板 (1)求电介质中的 , , 的大小及电介质表面的极化电荷 。 (2)求电容器两板板间的电势差; (3)画出电容器内的 线、 线及 线; (4)如果在插入 电介质平板后,保持电源接通。那么电介质中的 、 、 又为多大? 【解】(1)插入电介质平板之前,电容器极板间的场强 ,又 因此 。虽然插入介质。由于已断开电源所以 不变,由此我们可计算 、 、 ,由介质中高斯定理可知 插入介质板后两平行板间的电势差

红五古 - 城 g怪3-h (2)D线,豆线与户线如图b所示。 (3)由上面计算可知当断开电源在平行板电容器内插入介质后,电容器两板间电压下降了。 现在保持电源接通的情况下,电源对电容器就要充电。因此电容器两板上的自由电荷面密度 0就改变了。空气中的场强0也改变了,下面我们先计算在电源保持接通情况下的0。 2EU 得 8=1+8,)d 26n8,U 00=66= 由此: 1+s,)a D=8=8=1+5,a 2s6,U 2 U P=(g-0%8=s-12S g.+1d 夕【例13-2】设均匀极化的电介质球,极化强度为 (1)求极化电荷在球心处产生的场强。 (2)求证极化电荷在介质球内部产生的电场为均匀电场
(2) 线, 线与 线如图 b 所示。 (3)由上面计算可知当断开电源在平行板电容器内插入介质后,电容器两板间电压下降了。 现在保持电源接通的情况下,电源对电容器就要充电。因此电容器两板上的自由电荷面密度 就改变了。空气中的场强 也改变了,下面我们先计算在电源保持接通情况下的 。 得 由此: 【例 13-2】设均匀极化的电介质球,极化强度为 (1)求极化电荷在球心处产生的场强。 (2)求证极化电荷在介质球内部产生的电场为均匀电场

地图13-2 ▣兰13-2h 【解】(1)如题13-2阳取坐标x方向为极化电荷面密度 σ'=P,i=Pcos日 球面元=2R,m做d6的极化电荷9'在球心处产生的场强 指w0-费w0 Pcos02 46R° P =-【2os*0ma0-2 cos2acos日 方极化电荷的场豆的方向与P的方向相反 (2)既然介质球被均匀极化,介质中每个电偶极子平均地看来都在x方向发生了一个位移 1,对整个介质球看来相当于一个体电荷密度为P的带电球体发生了一个!的位移。在土P 相重合的地方不带电(为中性)而不重迭部分即界面上出现的电荷即为极化电荷。如图b。下 面我们就用这种模型来求证介质球内为均匀电场均匀带电体密度为士P的球体内任一点的场强 (参阅例11-4) 均匀带电体密度为一P的球体内任一点的场强 介质球均匀极化介质球内任意一点的场强由场强迭加原理,见图13-2b
【解】(1)如题 13-2a 取坐标 方向为极化电荷面密度 球面元 的极化电荷 在球心处产生的场强 方极化电荷的场 的方向与 的方向相反 (2)既然介质球被均匀极化,介质中每个电偶极子平均地看来都在 方向发生了一个位移 ,对整个介质球看来相当于一个体电荷密度为 的带电球体发生了一个 的位移。在 相重合的地方不带电(为中性)而不重迭部分即界面上出现的电荷即为极化电荷。如图 b。下 面我们就用这种模型来求证介质球内为均匀电场均匀带电体密度为 的球体内任一点的场强 (参阅例 11-4) 均匀带电体密度为 的球体内任一点的场强 介质球均匀极化介质球内任意一点的场强由场强迭加原理,见图 13-2b

设单位体积中电偶极子的个数为”,那么电荷密度P=9。所以上式 1, 12p =q三-2=-D)三36 38 36 380 38 得证 小 【例13-3】在真空中原来场强为。,今在这电场中放入一相对介电常数为5的介质 球,求这介质球内任意一点的场强。 【解】由上例可知均匀极化球中的极化电荷的场查为均匀场,现在介质球放在均匀场 瓦内。这场瓦和合场程仍为均匀场。设介质球的极化强度为户,由上例可知。 克=- 38 (1) 由电极化规律 P=,品豆=(8,-09 由场强迭加原 豆-豆。+ (3) (2)代入(1)得 3 (4) =成-与-1龙 (4)代入(3)得 83 移项整理得介质中任意点的场强 0 E 越图1a 号【例13-4】设w平面下方充满介电常数为的均匀介质,上方为真空。真空中0点与 MN平面的垂直距高为r,0点是垂足
设单位体积中电偶极子的个数为 ,那么电荷密度 。所以上式 得证。 【例 13-3】在真空中原来场强为 ,今在这电场中放入一相对介电常数为 的介质 球,求这介质球内任意一点的场强。 【解】由上例可知均匀极化球中的极化电荷的场 为均匀场,现在介质球放在均匀场 内。这场 和 合场强仍为均匀场。设介质球的极化强度为 ,由上例可知。 (1) 由电极化规律 (2) 由场强迭加原 理 (3) (2)代入(1)得 (4) (4)代入(3)得 移项整理得介质中任意点的场强 【例 13-4】设 MN 平面下方充满介电常数为 的均匀介质,上方为真空。真空中 O 点与 MN 平面的垂直距离为 r,O'点是垂足

(1)若将点电荷放在0处,求0点的场强, (2)若将点电荷放在0处,求0点极化电荷面密度及电位移矢量D 【解】(1)点电荷位于0点时,它在介质表面产生的电场沿介质表面,呈辐射状,无法向分 量,介质的极化强度也无法向分量,因此,除点电荷所在处外介质表面上无极化电荷。点电荷 所在处介质面上极化电荷与点电荷重合,它们在真空和介质中产生的合场强呈均匀辐射状。 以0为中心作半径为r的球形高斯面,因为电荷产生电场,因此球面上各点豆的量值相等, 而D的量值不等。根据介质中高斯定理,设真空中及介质中电位移矢量分别为P和方,有 物坐1?什: ∫面语+∫万桥=g 2nr'D +2wr'D=g D.=8E,D=8E 解得 2() (2)在0处点电荷场作用下,设0'处极化电荷面密度为',则据场强迭加原理,界面附近 真空中的场强: 担生131e (1) 面元附近介质中的场强: 8=4可+2 (2) 据边界条件,真空中和介质中电位移矢量相等: (3) 由上述三式解得0'处极化电荷面密度
(1)若将点电荷放在 O'处,求 O 点的场强 ; (2)若将点电荷放在 O 处,求 O'点极化电荷面密度及电位移矢量 。 【解】(1)点电荷位于 O'点时,它在介质表面产生的电场沿介质表面,呈辐射状,无法向分 量,介质的极化强度也无法向分量,因此,除点电荷所在处外介质表面上无极化电荷。点电荷 所在处介质面上极化电荷与点电荷重合,它们在真空和介质中产生的合场强呈均匀辐射状。 以 O'为中心作半径为 r 的球形高斯面,因为电荷产生电场,因此球面上各点 的量值相等, 而 的量值不等。根据介质中高斯定理,设真空中及介质中电位移矢量分别为 和 ,有 , 解得 (2)在 O 处点电荷场作用下,设 O'处极化电荷面密度为 ,则据场强迭加原理,界面附近 真空中的场强: (1) 面元附近介质中的场强: (2) 据边界条件,真空中和介质中电位移矢量相等: (3) 由上述三式解得 O'处极化电荷面密度

(8-1g 。=E+020 (4) (8.-1g o=(e.+020 (4) 将(4)式代入(1)式,得 +a 垂足0的电位移矢量 D=e8,=688=2og+d 8.4 号【例13=5】如图a所示,静电除尘的实验装置中,内有半径为的金属丝,外有半径 为凡金属简,整个装置细而长。在做实验时,金属丝和金属筒之间加上高电压,当烟灰往 上冒的时候,在电场力的作用下产生位移极化,设烟尘极化可近似看作为电偶极矩为”的电 偶极子,并设在运动过程中它的电矩不变,且电偶极子的方向与电场方向平行。 (1)试分析烟灰在圆柱简内将如何运动。 (2)求烟灰在离中心线处所受的电场力。 (3)求烟灰从运动到?过程中电场力对烟灰所作的功
(4) (4) 将(4)式代入(1)式,得 垂足 O'的电位移矢量 。 【例 13-5】如图 a 所示,静电除尘的实验装置中,内有半径为 的金属丝,外有半径 为 金属筒,整个装置细而长。在做实验时,金属丝和金属筒之间加上高电压 ,当烟灰往 上冒的时候,在电场力的作用下产生位移极化,设烟尘极化可近似看作为电偶极矩为 的电 偶极子,并设在运动过程中它的电矩不变,且电偶极子的方向与电场方向平行。 (1)试分析烟灰在圆柱筒内将如何运动。 (2)求烟灰在离中心线 处所受的电场力。 (3)求烟灰从 运动到 过程中电场力对烟灰所作的功
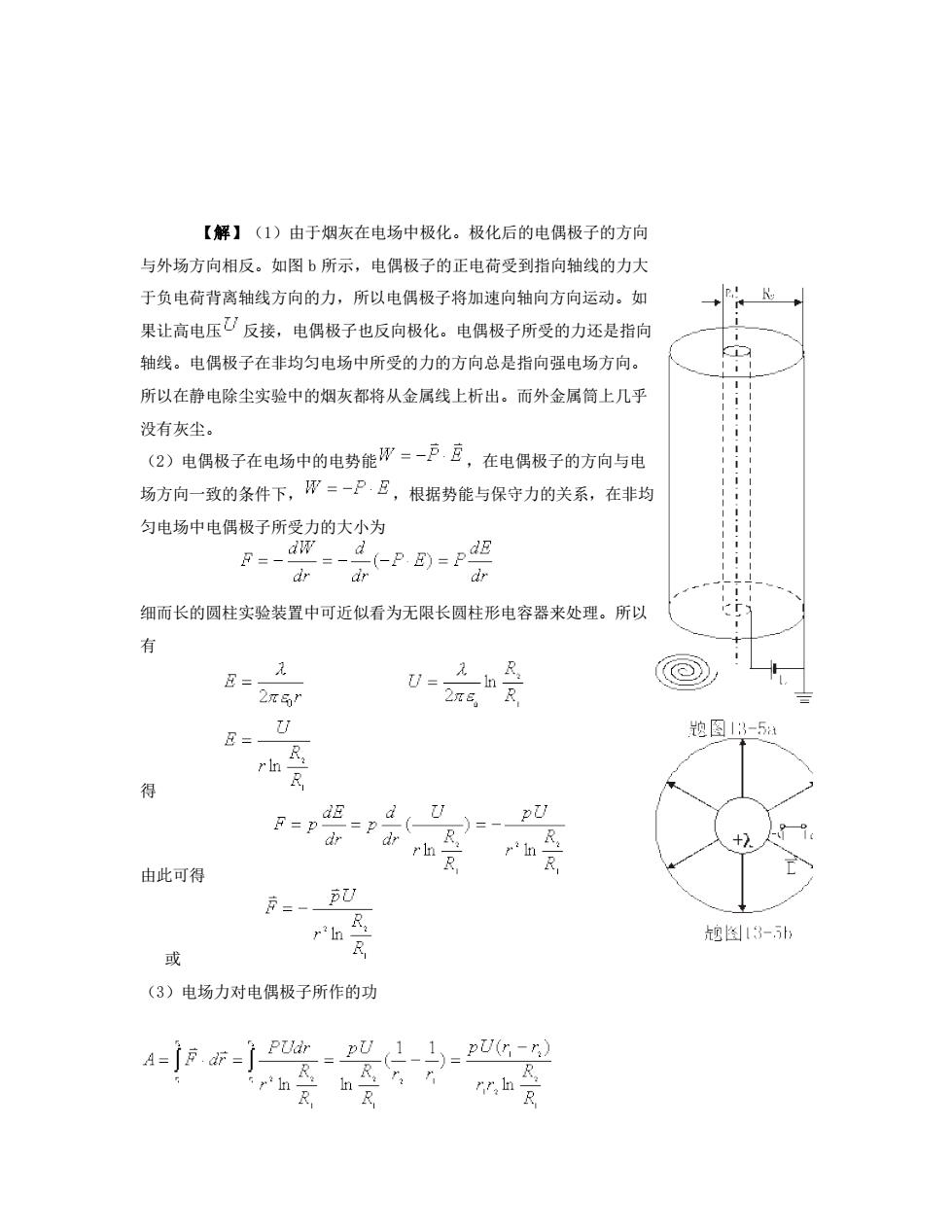
【解】(1)由于烟灰在电场中极化。极化后的电偶极子的方向 与外场方向相反。如图b所示,电偶极子的正电荷受到指向轴线的力大 于负电荷背离轴线方向的力,所以电偶极子将加速向轴向方向运动。如 果让高电压反接,电偶极子也反向极化。电偶极子所受的力还是指向 轴线。电偶极子在非均匀电场中所受的力的方向总是指向强电场方向。 所以在静电除尘实验中的烟灰都将从金属线上析出。而外金属筒上几乎 没有灰尘。 (2)电偶极子在电场中的电势能W=-户豆,在电偶极子的方向与电 场方向一致的条件下,W=一P·区,根据势能与保守力的关系,在非均 匀电场中电偶极子所受力的大小为 细而长的圆柱实验装置中可近似看为无限长圆柱形电容器来处理。所以 R (@ 图1}-5a R 得 r B-p dr 4(U )--p0 +7. 由此可得 京=- 0 @图3-h 或 (3)电场力对电偶极子所作的功 A=jFm=jP-p吧2-马=pc-
【解】(1)由于烟灰在电场中极化。极化后的电偶极子的方向 与外场方向相反。如图 b 所示,电偶极子的正电荷受到指向轴线的力大 于负电荷背离轴线方向的力,所以电偶极子将加速向轴向方向运动。如 果让高电压 反接,电偶极子也反向极化。电偶极子所受的力还是指向 轴线。电偶极子在非均匀电场中所受的力的方向总是指向强电场方向。 所以在静电除尘实验中的烟灰都将从金属线上析出。而外金属筒上几乎 没有灰尘。 (2)电偶极子在电场中的电势能 ,在电偶极子的方向与电 场方向一致的条件下, ,根据势能与保守力的关系,在非均 匀电场中电偶极子所受力的大小为 细而长的圆柱实验装置中可近似看为无限长圆柱形电容器来处理。所以 有 得 由此可得 或 (3)电场力对电偶极子所作的功