
第16章变化电磁场 夕一、电磁感应定律 磁通变化的两类原因:回路变化和磁场变化 1、法拉弟电磁感应定律: 8= 尘 du 或 式中w=师 称磁通链。 2、感应电量: 夕二、动生电动势和感生电动势 1、动生电动势:因回路变化产生的电磁感应。 非静电场强: [导体回路 s=fo×a 一段导体s=jo×)i 动生电动势: 能量转换:洛仑兹力的一个分力做负功吸收外界能量,另一分力做正功输出电能。 2、感生电动势:因磁场变化产生电磁感应。 感应电场:起源于变化磁场。 ,有旋性。 a,=0 无源性。 闭合回路:g=克 一段电路:c=∫鸟 感应电动势 三、自感和互感
第 16 章 变化电磁场 一、电磁感应定律 磁通变化的两类原因:回路变化和磁场变化。 1、法拉弟电磁感应定律: 或 式中 ,称磁通链。 2、感应电量: 二、动生电动势和感生电动势 1、动生电动势:因回路变化产生的电磁感应。 非静电场强: 动生电动势: 能量转换:洛仑兹力的一个分力做负功吸收外界能量,另一分力做正功输出电能。 2、感生电动势:因磁场变化产生电磁感应。 感应电场:起源于变化磁场。 ,有旋性。 ,无源性。 感应电动势 三、自感和互感

1、自感应: 4:9-号 =-- 自感电动势: d 当线圈形状不变时,即L不变 2、互感应 M=V=Va 互感系数: 4112 感电烧.必登-出 dt 两线圈形状和相对位置不变时,即M不变 1=-dy dt =M当 dt 3、回路藕合:M=K马 式中K为耦合系数 4、电感的串并联 (1)串联乙=乙1+乙±2 两电感顺接取“+”号,反接取“一”号。 LL2-M (2)并联 -2M 两电感顺接取“一”号,反接取“+”号。 夕四、磁能 1、电感磁能: 自品 互感磁场:土M, 总磁能: 2、磁场能量
1、自感应: 自感系数: 自感电动势: 当线圈形状不变时,即 L 不变 2、互感应 互感系数: 互感电动势: 两线圈形状和相对位置不变时,即 M 不变 3、回路藕合: 式中 K 为耦合系数 4、电感的串并联 (1)串联 两电感顺接取“+”号,反接取“—”号。 (2)并联 两电感顺接取“—”号,反接取“+”号。 四、磁能 1、电感磁能: 自感磁能: 互感磁场: 总磁能: 2、磁场能量:

磁能密度: 24 W=wdΨ 磁场能量: 夕五、暂态过烟 在暂态过程中,外加跃变电压后,电路中电流或电压不发生突变,而是逐渐变化,趋于稳态。 1、LR电路:由于线圈中自感电动势的反抗,回路中电流不能突变。 2、C电路:由于电容器中电场的反抗,电容上电压不能突变。 两种电路的特性对照表 R电路 RC电路 暂态过程 滋长过程: 充电过程: -R=0 -名=0 a-e U.=1-ec) 初态:I=O,L起断路作用 1 初态: R,C起短路作用 i=s R,L起短路作用 终态:I=0,C起断路作用 稳态: 衰减过程: R9+9-0 +0 8=0 6=0, 时间常数 F= r=RC 储能元件 储磁能: 9 大、感应电场 变化的磁场激发的电场称为感应电场,感应电场的电力线为闭合曲线因此感应电场也称涡旋电 场。 1、感应电场与变化磁场的关系
磁能密度: 磁场能量: 五、暂态过程 在暂态过程中,外加跃变电压后,电路中电流或电压不发生突变,而是逐渐变化,趋于稳态。 1、LR 电路:由于线圈中自感电动势的反抗,回路中电流不能突变。 2、RC 电路:由于电容器中电场的反抗,电容上电压不能突变。 两种电路的特性对照表 LR 电路 RC 电路 暂态过程 滋长过程: 初态:I=0,L 起断路作用 稳态: ,L 起短路作用 充电过程: 初态: ,C 起短路作用 终态:I=0,C 起断路作用 衰减过程: , , 时间常数 储能元件 储磁能: 储电能: 六、感应电场 变化的磁场激发的电场称为感应电场,感应电场的电力线为闭合曲线因此感应电场也称涡旋电 场。 1、感应电场与变化磁场的关系
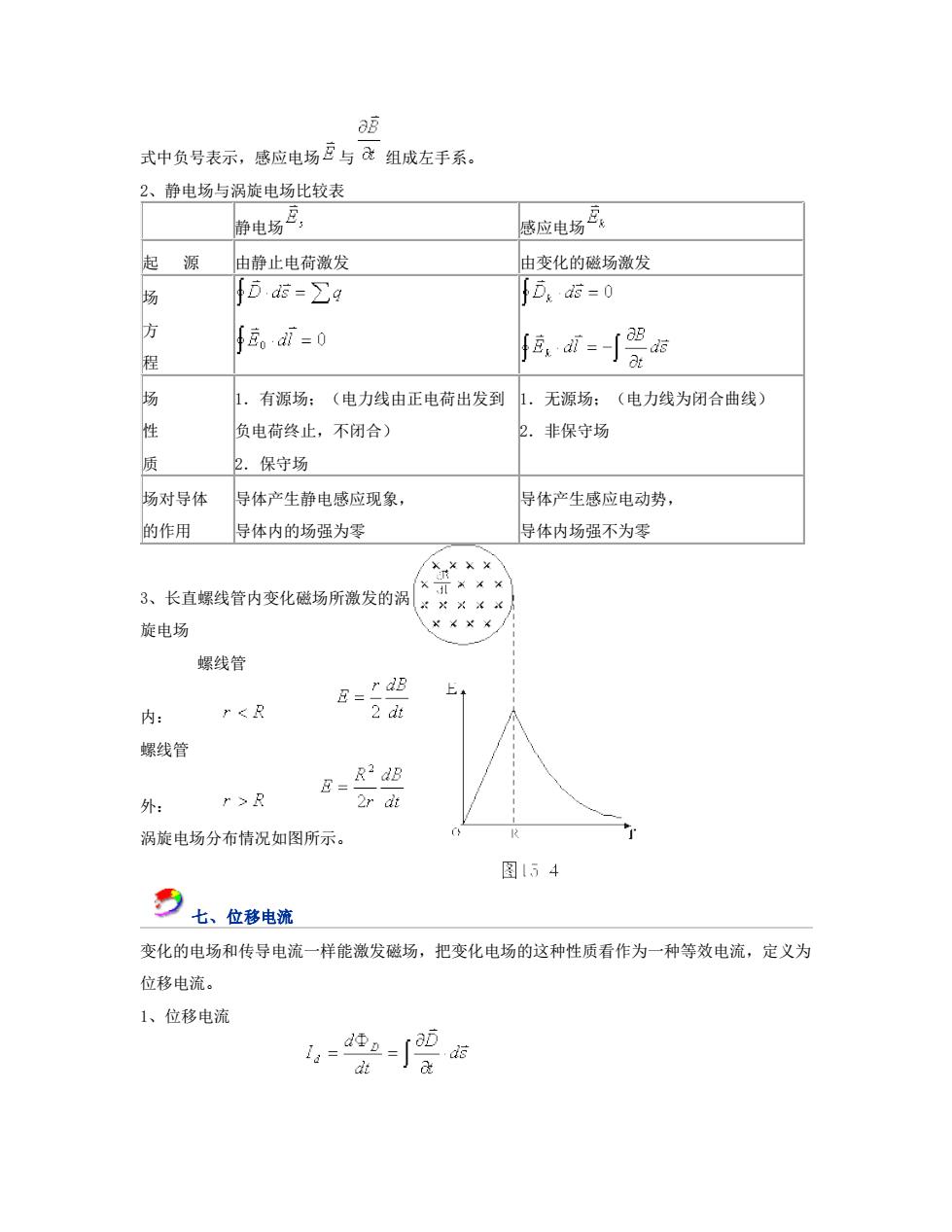
式中负号表示,感应电场巨与组成左手系 2、静电场与涡旋电场比较表 静电场巴, 感应电场 起源 由静止电荷激发 由变化的磁场激发 D·ds=∑g D-0 程 兵堂 1.有源场:(电力线由正电荷出发到 无源场:(电力线为闭合曲线) 负电荷终止,不闭合) 非保守场 质 2.保守场 场对导体 导体产生静电感应现象 导体产生感应电动势, 的作用 导体内的场强为零 导体内场强不为零 3、长直螺线管内变化磁场所激发的涡 旋电场 螺线管 上+ 内: "<R 8= 螺线管 Zr dt 涡旋电场分布情况如图所示。 图154 夕七、位移电流 变化的电场和传导电流一样能激发磁场,把变化电场的这种性质看作为一种等效电流,定义为 位移电流。 1、位移电流
式中负号表示,感应电场 与 组成左手系。 2、静电场与涡旋电场比较表 静电场 感应电场 起 源 由静止电荷激发 由变化的磁场激发 场 方 程 场 性 质 1.有源场;(电力线由正电荷出发到 负电荷终止,不闭合) 2.保守场 1.无源场;(电力线为闭合曲线) 2.非保守场 场对导体 的作用 导体产生静电感应现象, 导体内的场强为零 导体产生感应电动势, 导体内场强不为零 3、长直螺线管内变化磁场所激发的涡 旋电场 螺线管 内: 螺线管 外: 涡旋电场分布情况如图所示。 七、位移电流 变化的电场和传导电流一样能激发磁场,把变化电场的这种性质看作为一种等效电流,定义为 位移电流。 1、位移电流

位移电流密度 -9 2、传导电流与位移电流比较表 传导电流20 位移电流 激发磁场 遵守安培环路定律 遵守安培环路定律 的规律 庄d=lo -=增 产生的原因 电荷在导体中宏观定向运动产生。 由变化电场所激发与电荷的定向运动 无关。 存在场所 导体 真空、介质及导体 电流方向 与电场方向相同 与电场的变化方向相同 热效应 遵守焦耳楞次定律 在导体及真空中无热效应, (在介质中,高频情况下能产生极化 热现象,但不遵守焦耳楞次定律 3、圆形平行板电容器内变化电场所 产生的磁场 电容器内 rR 位移电流所产生磁场的分布情况如 图所示。 ☒15-5 号八、变化电藏场蒸本提排 1、电磁场的统一性 变化的电场、磁场不能独立存在。 ,i- (1)变化电场激发磁场: ∫i=∫ (2)变化磁场激发电场:
位移电流密度 2、传导电流与位移电流比较表 传导电流 位移电流 激发磁场 的规律 遵守安培环路定律 遵守安培环路定律 产生的原因 电荷在导体中宏观定向运动产生。 由变化电场所激发与电荷的定向运动 无关。 存在场所 导体 真空、介质及导体 电流方向 与电场方向相同 与电场的变化方向相同 热效应 遵守焦耳楞次定律 在导体及真空中无热效应。 (在介质中,高频情况下能产生极化 热现象,但不遵守焦耳楞次定律 3、圆形平行板电容器内变化电场所 产生的磁场 电容器内 电容器外 位移电流所产生磁场的分布情况如 图所示。 八、变化电磁场基本规律 1、电磁场的统一性 变化的电场、磁场不能独立存在。 (1)变化电场激发磁场: (2)变化磁场激发电场:

2、麦克斯韦方程组 微分形 必 [万ds=g (1)通量方程: 7.i=p 7i=0 7xi=-丽 (2)环流方程: 7=盟 麦克斯韦方程组是电磁场的普遍规律,它预言电磁波的存在和光的电磁本性。 3、电磁理论发展和示意方框图 方合】非 11甲 传场产1原钟 华产立补 玄培环流了坪 传场严1 、0打 小北流湖切 巾场 口流让然件 变化中做发 ,移电流但设
2、麦克斯韦方程组 微分形 式 (1)通量方程: (2)环流方程: 麦克斯韦方程组是电磁场的普遍规律,它预言电磁波的存在和光的电磁本性。 3、电磁理论发展和示意方框图

第16章变化电磁场 号【例16-1】如图161a两无限长平行光滑导轨间距为,导轨与水平面成角放置,整 个装置处在磁感应强度均匀为的磁场之中,B的方向垂直地面向上,两导轨间串接了电阻 R及电动势为的电源。滑杆b质量为m,滑杆初速为零,求滑杆下滑速度随时间的关系。 并由此求滑杆的极限速度。 R 0 红图1行-1a 题图161b 【解】滑杆在下滑过程中除受重力之外还受到安培力的作用,这里应注意到安培力4的方向 不是沿斜面方向,而是垂直于B与杆ab组成的平面,见图16-1b,由此列出牛顿运动方程: 洲gm6-P4cos6=m dt (1) 流过滑杆b的电流除了电源电动势8的作用,还要考虑滑杆本身产生的感生电动势 号=sm(90°+8)=Blvcosa 由判别可知气的方向与相同,所以流过滑杆b的电流 1=5+6=s+Blvco:0 R R 由此得安培力 FA=Bm=B.g+iucos日 (2) 将(2)式代入(1)式得: g如8-5+i8co8=m出 R (3)
第 16 章 变化电磁场 【例 16-1】如图 16-1a 两无限长平行光滑导轨间距为 ,导轨与水平面成 角放置,整 个装置处在磁感应强度均匀为 的磁场之中, 的方向垂直地面向上,两导轨间串接了电阻 R 及电动势为 的电源。滑杆 ab 质量为 m,滑杆初速为零,求滑杆下滑速度随时间的关系。 并由此求滑杆的极限速度。 【解】滑杆在下滑过程中除受重力之外还受到安培力的作用,这里应注意到安培力 的方向 不是沿斜面方向,而是垂直于 B 与杆 ab 组成的平面,见图 16-1b,由此列出牛顿运动方程: (1) 流过滑杆 ab 的电流除了电源电动势 的作用,还要考虑滑杆本身产生的感生电动势 由判别可知 的方向与 相同,所以流过滑杆 ab 的电流 由此得安培力 (2) 将(2)式代入(1)式得: (3)

du (gm0-则8cos8-82cos28 分离变量积分: mgRsin e 可得 当:→切时滑杆到达极限速 mgRsin 8 dv=0 如果只要求极限速度=的话,那么 的条件直接代入(3)就可求得。 号【例16-2】在上例条件下,如将号轨间的电阻换成电容C,并设回路中的电阻很小可忽 略不计,滑杆下滑过程中电容C不击穿,试计算滑杆下滑速度随时间的关系。 【解】滑杆在下滑过程中除了受重力之外同样也受到安培力的作用,这里流 过滑杆的电流是b杆的感生电动势对电容充电的电流为 1四 作用在滑杆上的安培力 FA=BII=BI cU (1) 由于忽略回路电阻R,所以电容器两端的电压即为滑杆的感生电动势 U=BIU (2) 再由牛顿运动方程 mg-Fa=ma 将(2)式代入(1)式再代入(3)式,得 mg-Bic (Bu)=ma 题162 注意到式中业 ,上式可化为: mg-B2Pca=ma a= 解得滑杆下滑时的加速度 m+B2p2c 由此可知滑杆以匀加速下滑,任一时刻的速度
分离变量积分: 可得 当 时滑杆到达极限速度 如果只要求极限速度 的话,那么 的条件直接代入(3)就可求得。 【例 16-2】在上例条件下,如将导轨间的电阻换成电容 C,并设回路中的电阻很小可忽 略不计,滑杆下滑过程中电容 C 不击穿,试计算滑杆下滑速度随时间的关系。 【解】滑杆在下滑过程中除了受重力之外同样也受到安培力的作用,这里流 过滑杆的电流是 ab 杆的感生电动势对电容充电的电流为 作用在滑杆上的安培力 (1) 由于忽略回路电阻 R,所以电容器两端的电压即为滑杆的感生电动势 (2) 再由牛顿运动方程 (3 ) 将(2)式代入(1)式再代入(3)式,得 注意到式中 ,上式可化为: 解得滑杆下滑时的加速度 由此可知滑杆以匀加速下滑,任一时刻的速度

mgt v=at=- %+B22℃ 在这种情况下,滑杆就不存在极限速度。请读者是否能从物理过程来分析一 下滑杆在这种情况下为什么不存在极限速度。 号【例16-3】如图16-3a图中ebca电略有电阻R,其中be段的一部分绕成圆圈形, 圆圈区域有一与回略平面垂直的均匀磁场B,在圆圈形导线的一边施加恒力,由于a端固 定,假定圆圈开始的半经为0,并维持以圆形的方式收缩,设导线非常柔软,忽略导线的质 量,问需要多长的时间圆形部分完全闭合? E ···4 + 题图163a @图163h 【解】由于圆圈形导线在收缩过程中,通过圆圈形面积上的磁通量减少,线圈内要产生感应电 流:。感应电流在磁场中就要受到安培力,安培力方向可以判别是沿半径方向向外,由于忽略 导线质量,导线所受的外力F,导线张力F与安培力三者平衡,如图16b所示,并如图取坐 =,Bdl,cos日=,Br cosQie 由于对称性,半圆弧产生的安培力合力 F=1,Bcos8=24 由对称性及力平衡条件 F-F FA=8+8 得: F=1:B (1) 由于外力作用,r在收缩过程中回路内产生的感应电流: 1d0.-2o8 R R dt 将代入(1)式得: =受的2产 R dt
在这种情况下,滑杆就不存在极限速度。请读者是否能从物理过程来分析一 下滑杆在这种情况下为什么不存在极限速度。 【例 16-3】如图 16-3a 图中 abcda 电路有电阻 R,其中 bc 段的一部分绕成圆圈形, 圆圈区域有一与回路平面垂直的均匀磁场 B,在圆圈形导线的一边施加恒力 F,由于 a 端固 定,假定圆圈开始的半径为 ,并维持以圆形的方式收缩,设导线非常柔软,忽略导线的质 量,问需要多长的时间圆形部分完全闭合? 【解】由于圆圈形导线在收缩过程中,通过圆圈形面积上的磁通量减少,线圈内要产生感应电 流 。感应电流在磁场中就要受到安培力,安培力方向可以判别是沿半径方向向外,由于忽略 导线质量,导线所受的外力 F,导线张力 F'与安培力三者平衡,如图 16-3b 所示,并如图取坐 标,电流元 所受的安培力在 x 方向上的分量: 由于对称性,半圆弧产生的安培力合力 由对称性及力平衡条件 得: (1) 由于外力作用,r 在收缩过程中回路内产生的感应电流: 将 代入(1)式得:

得。 dt=- 2xB2,2 RF 由初始条件 t=0,r=%,=t,r=0 =-「28,2 =282 两边积分 3 号【例16-4】在磁感应强度为5的均匀磁场内,有一面积为S的矩形线框,线框回略的电 阻为R(忽略自感),线框绕其对称轴00以匀角速度旋转(如题图16-4所示)。 (1)求在如图位置时线框所受的磁力炬为多大? (2)为维持线框匀角速度转动,外力矩对线框每转一周需作的功为多少? 【解】(1)在任一位置时通过线框的磁通量 =BS cosp (1) 在线框内产生的感生电动势 8= at -BS sn o de-BSusn p d (2) 流过线框的感应电流 0 R (3) p-18-E'umo 线框的磁矩 R 线框所受的磁力矩的大小为 M =PB sin =an B in =B in R y图6-4 写成矢量形式 R 也就是磁力矩的方向(产×B的方向)与西方向相反。 (2)方法一,要维持线框作均匀速转动,必须作用在线框上的合外力矩M和磁力矩证:平 衡,就是 M+M=0 亚=-成n= -Oisin2 或 R 外力矩对线框每转一周所作的功:
得: 由初始条件 , , , 两边积分 【例 16-4】在磁感应强度为 的均匀磁场内,有一面积为 S 的矩形线框,线框回路的电 阻为 R(忽略自感),线框绕其对称轴 OO'以匀角速度 旋转(如题图 16-4 所示)。 (1)求在如图位置时线框所受的磁力矩为多大? (2)为维持线框匀角速度转动,外力矩对线框每转一周需作的功为多少? 【解】(1)在任一位置时通过线框的磁通量 (1) 在线框内产生的感生电动势 (2) 流过线框的感应电流 (3) 线框的磁矩 线框所受的磁力矩的大小为 写成矢量形式 也就是磁力矩的方向( 的方向)与 方向相反。 (2)方法一,要维持线框作均匀速转动,必须作用在线框上的合外力矩 M 和磁力矩 平 衡,就是 或 外力矩对线框每转一周所作的功: