
第4章动量和角动量 一、动量定理 1、动量 和2 均为描述机械运动的状态量,但两者有重要区别:6m)是物体之间传递机 械运动的量度: 6(5mu) 是物体的机械运动形式与其他运动形式相互转换的一种量度。 2、冲量:冲量是力对时间的累积,导致机械运动的传递。 7【a恒力 7=日: 冲击力1= 3、动量定理: 质点,「动=加i-m吗=-元 质点系: ∑d=∑%店-工%=产-列 5 二、动量守恒定律 =0=P 3=0p=P ∑月=0,方= 矢量式: 分量式: 8=0= 利用某一方向上的动量守恒分量式常可简捷地解决力学问题。 夕三、范推同器 满足动量守恒定律:洲巧+洲可2=洲0+洲心20 满足牛顿规则(沿碰撞方向):凸-4=0-0)。 「e=0,完全非弹性碰撞; ee=1,弹性碰撞; 恢复系数 0<e<1,非弹性碰撞。 日、火餐飞行同
第 4 章 动量和角动量 一、动量定理 1、动量 和 均为描述机械运动的状态量,但两者有重要区别: 是物体之间传递机 械运动的量度; 是物体的机械运动形式与其他运动形式相互转换的一种量度。 2、冲量:冲量是力对时间的累积,导致机械运动的传递。 3、动量定理: 质点: 。 质点系: 二、动量守恒定律 矢量式: ; 分量式: 利用某一方向上的动量守恒分量式常可简捷地解决力学问题。 三、碰撞问题 满足动量守恒定律: 满足牛顿规则(沿碰撞方向); 。 恢复系数 四、火箭飞行问题

箭体运动方程: =加空 d。 火箭飞行速度:U=4h(从,从) 号五、质心,质心是质点系中运功特滴单,能代表质点系整体运动的箱殊点。 1、质心位置 元=∑m元1M 2、质点系动量 %马= 3、质心运动定理 ∑R=Mg=版 公月=0,“=恒矢量 步 六、质点角动量及其规律 1、角动量:角动量是与各质点动量和参考点位置有关的状态量。 (1)质点:艺=广×州心. 乙=∑店×洲店 (2)质点系: 2、角动量规律 =rx京- (1)转动动力学方程: (2)角动量定理:∫=1-乙, (3)角动量守恒定律:亚=0,乙=乙】
箭体运动方程: 。 火箭飞行速度: 五、质心:质心是质点系中运动特别简单,能代表质点系整体运动的特殊点。 1、质心位置 或 。 2、质点系动量 3、质心运动定理 六、质点角动量及其规律 1、角动量: 角动量是与各质点动量和参考点位置有关的状态量。 (1)质点: 。 (2)质点系: 2、角动量规律 (1)转动动力学方程: 。 (2)角动量定理: (3)角动量守恒定律:

第4章动量和角动量 【例4-1】如题图4-1a所示,斜面长5米,高3米,斜面的下端与一水平面相接,一 物块从斜面上端由静止开始下滑,物块与斜面及平面的廉擦系数均为“,(“=03),求物 块从斜面顶端由静止开始下滑,滑到平面上后还能在平面上滑行多长距离?(尽取10 mis') 【解】设物块滑到斜面下端的速度大小为,根据功能原理 一gc08=7mu-mg 得4=2g-2g/c0s6=V2×10x3-2×0.3x10x5x08=6m16 mg 题图1-1) 因M-1h 这里应注意的是马的方向是沿着斜面的,当物块通过转角处,速度变为水平方向,物体的动 量发生了改变,则必定受到外力的冲量。 参阅题图4-1b。在垂直方向('方向)应用动量原理: ∫(aW-wg)=0-(←mysm) 由于物体通过转角处的时间很短,物体与水平面碰撞瞬间的正压力N>洲g,上式可写成: 2at=n心sm日 (1) 再在水平方向(x方向)上应用动量原理: -=m心2-mcos日 (2) 由于了=W所以 -ft=-Wt=-simn日 (3) 比较(2)、(3)式得: -m日=m2-m4cos日 由此解得,得通过转角后,物块在水平面上开始运动的速度
第 4 章 动量和角动量 【例 4-1】如题图 4-1a 所示,斜面长 5 米,高 3 米,斜面的下端与一水平面相接,一 物块从斜面上端由静止开始下滑,物块与斜面及平面的摩擦系数均为 ,( )。求物 块从斜面顶端由静止开始下滑,滑到平面上后还能在平面上滑行多长距离?( 取 10 ) 【解】设物块滑到斜面下端的速度大小为 ,根据功能原理 得 这里应注意的是 的方向是沿着斜面的,当物块通过转角处,速度变为水平方向,物体的动 量发生了改变,则必定受到外力的冲量。 参阅题图 4-1b。在垂直方向( 方向)应用动量原理: 由于物体通过转角处的时间很短,物体与水平面碰撞瞬间的正压力 ,上式可写成: (1) 再在水平方向( 方向)上应用动量原理: (2) 由于 所以 (3) 比较(2)、(3)式得: 由此解得,得通过转角后,物块在水平面上开始运动的速度
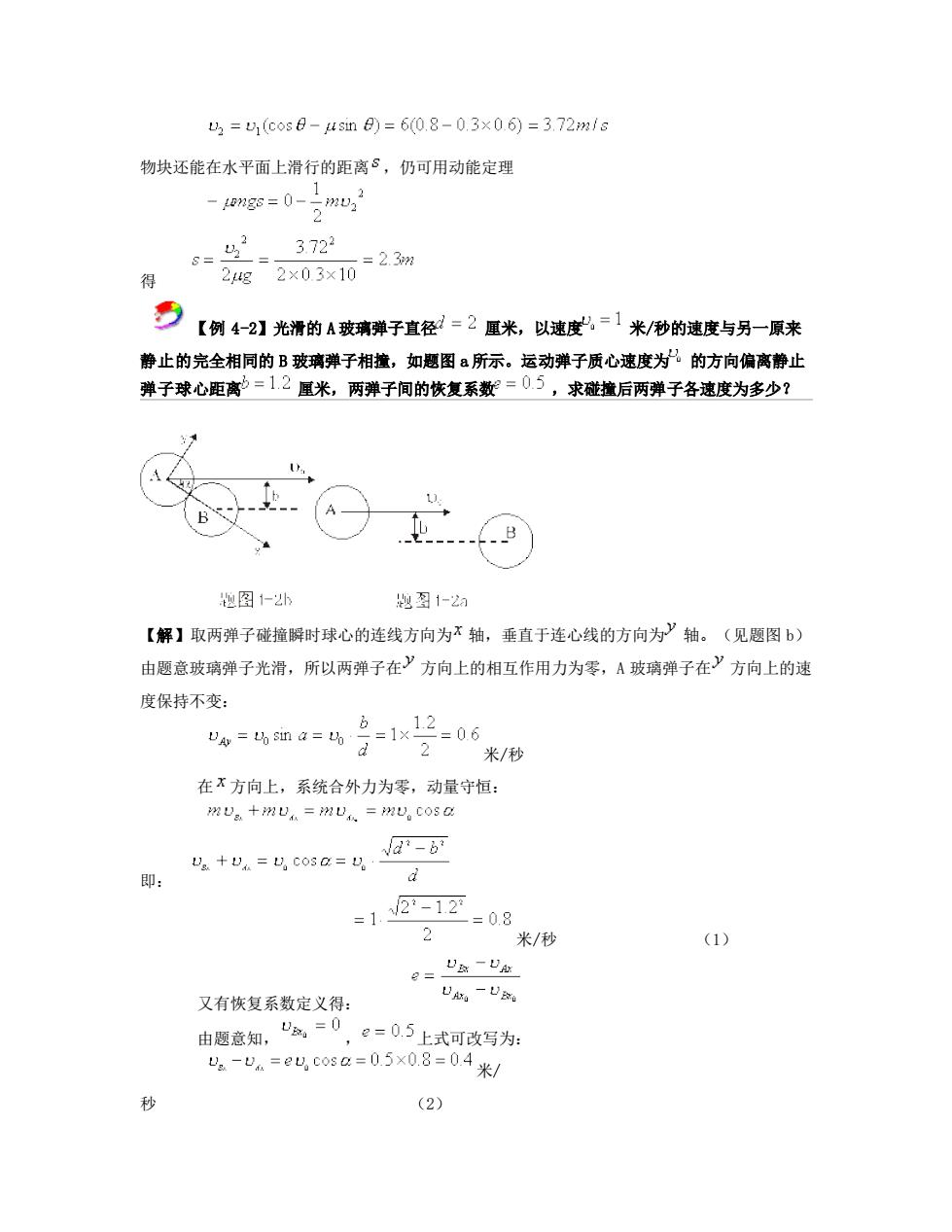
2=1(cos日-asim=60.8-03×06)=3.72m1s 物块还能在水平面上滑行的距离$,仍可用动能定理 3722 得 2g2×03x10=23 号【例2】光清的A玻精弹子直径=2显米,以速美=1米带的速支与月原来 静止的完全相同的B玻璃弹子相撞,如题图a所示。运动弹子质心速度为的方向偏离静止 弹子球心距离之=12厘米,两弹子间的恢复系数=05,求碰撞后两弹子各速度为多少? 物图1-2 【解】取两弹子碰撞瞬时球心的连线方向为x轴,垂直于连心线的方向为》轴。(见题图b) 由题意玻璃弹子光滑,所以两弹子在》方向上的相互作用力为零,A玻璃弹子在》方向上的速 度保持不变: b 米/秒 在不方向上,系统合外力为零,动量守恒: 为Ua十洲U=渊.=U。COs@ d°-b a+U=cosa=. d =1212 =08 2 米/秒 (1) e-UR-Ug 又有恢复系数定义得: DA.-U8 由题意知,,=0,=05上式可改写为 4-=euco8=05×0,8=04米/ (2)
物块还能在水平面上滑行的距离 ,仍可用动能定理 得 【例 4-2】光滑的 A 玻璃弹子直径 厘米,以速度 米/秒的速度与另一原来 静止的完全相同的 B 玻璃弹子相撞,如题图 a 所示。运动弹子质心速度为 的方向偏离静止 弹子球心距离 厘米,两弹子间的恢复系数 ,求碰撞后两弹子各速度为多少? 【解】取两弹子碰撞瞬时球心的连线方向为 轴,垂直于连心线的方向为 轴。(见题图 b) 由题意玻璃弹子光滑,所以两弹子在 方向上的相互作用力为零,A 玻璃弹子在 方向上的速 度保持不变: 米/秒 在 方向上,系统合外力为零,动量守恒: 即: 米/秒 (1) 又有恢复系数定义得: 由题意知, , 上式可改写为: 米/ 秒 (2)

解(1)、(2)式得: =0.2米/秒: v=0.6米/秒。 由此知两球碰撞后的速度分别为: 西4=(02+0.6米/秒 立影=06行米/秒 9 【例4-3】试计算半径为R,顶角为的匀质扇形板的质心位置。 【解】我们先把大扇形分割成很多△口很小的顶角相同的小扇形,顶角很小的扇形就非常接近 于三角形,三角形的质心位于中线的3位置上,当顶角△趋向于零时,各扇形的质心位于就 分布在三不的圆上,因此我们求速扇形的质心只要求半轻了,来相为公的匀质可 r=-R 弧的质心即可。设这圆弧单位长度的质量为。 x dm=rcose Arde=ar'cose de 根据质心计算公式: [a2cosaie = = r.2a 作为特例,如要计算匀质半圆薄板的质心,只需将2=2,代入上式 可: 越1-3图 2 4R 号【例】质蛋为业的人手里本着质蛋为▣的物体,此人用与地平镜彩的惠雀 向前跳去,当他到达最高点时,把物体以相对于自己以速度u向后抛出,问由于物体的抛 出,他跳过的距离与不抛物体时相比可增加多少?
解(1)、(2)式得: 米/秒; 米/秒。 由此知两球碰撞后的速度分别为: 米/秒 米/秒 【例 4-3】试计算半径为 R,顶角为 的匀质扇形板的质心位置。 【解】我们先把大扇形分割成很多 很小的顶角相同的小扇形,顶角很小的扇形就非常接近 于三角形,三角形的质心位于中线的 位置上,当顶角 趋向于零时,各扇形的质心位于就 分布在 的圆弧上,因此我们求该扇形的质心只要求半径 ,张角为 的匀质圆 弧的质心即可。设这圆弧单位长度的质量为 。 根据质心计算公式: 作为特例,如要计算匀质半圆薄板的质心,只需将 ,代入上式即 可: 【例 4-4】质量为 M 的人,手里拿着质量为 m 的物体,此人用与地平线成 的速度 向前跳去,当他到达最高点时,把物体以相对于自己以速度 u 向后抛出,问由于物体的抛 出,他跳过的距离与不抛物体时相比可增加多少?

【解】方法一,如题图4-4a,取地面坐标系,用动量守 恒定律求解: 人不向后抛出物体,所能跳过的距离: 式中T为人跳离地面的时间。 由: y=4Tma-587=0 T=20o sin 解得: (T=0删去》 可得: R-2 sin a cosam 2 .-1 人在最高点以相对于自己u的速度向后抛出物体的过程"T 中,参阅题图a,应用动量守恒原理。 MV+m(v-u)=(m+M)vo cosa 可得人以相对于自己u的速度向后抛出物体后人的速 度 V=D.cosa+m+证 4 见1业 可见人比不抛出物体时速度乌co:口增加了速 度: AV=m+M 因此人在抛出物体后多跳过的距离: AR=AV I=Av.I mu to sin c 2洲+Mg 方法二,质心坐标系中应用动量守恒定律: 2U+2W=0 V-v=u V= 可得: 厂物+M 1=to sin a 在下落时间 名过程中,人相对于质心运动的距离,即为人比不抛出物体多跳过的距
【解】方法一,如题图 4-4a,取地面坐标系,用动量守 恒定律求解: 人不向后抛出物体,所能跳过的距离: 式中 T 为人跳离地面的时间。 由: 解得: ( 删去) 可得: 人在最高点以相对于自己 u 的速度向后抛出物体的过程 中,参阅题图 a,应用动量守恒原理。 可得人以相对于自己 u 的速度向后抛出物体后人的速 度: 可见人比不抛出物体时速度 增加了速 度: 因此人在抛出物体后多跳过的距离: 方法二,质心坐标系中应用动量守恒定律: 可得: 在下落时间 过程中,人相对于质心运动的距离,即为人比不抛出物体多跳过的距

离: △R=V=m+Mg mu o sin c 方法三,应用质心运动定律求解: 由于内力不改变质心原来运动的轨迹,由在质心C落地位置为人不抛出物体时原来落地位置 现人以相对于自己速度u抛出物体m时,在下落时间过程中,人M与物体m之间的距离: 1=ut=u.tosma g 由质心位置公式知,质量为M的人离质心距离为: △R=1 2224U.gn2 m+M (6+g 号【例46如至所示,一质量为的的质储条,长为手持其上汽下确桌面费 触。现使链条自静止释成落于桌面,试从下述三种不同的规律出发,计算链条下落距离时桌 面对链条的作用力: (1)动量规律; (2)质心运动规律: (3)变质量动力学规律: 【解】这是一个连续分布的柔性质点系,可以选择不同的部分作为研究对象,也可以从不同的 角度求解。 7777777777717777777 题图4-5a 题图4-5b 题图4-5c 方法一,运用动量规律求解。取如图b坐标。设时刻下落至桌面部分的链条长为》,质量为 2 至+止时间内落到桌面上的链务质量为 ,其速度由”减到0。选取已下 落至桌面以及时间内下落至桌面的少+段链条为研究对象。由于链条自由下落,y+
离: 方法三,应用质心运动定律求解: 由于内力不改变质心原来运动的轨迹,由在质心 C 落地位置为人不抛出物体时原来落地位置, 现人以相对于自己速度 u 抛出物体 m 时,在下落时间 过程中,人 M 与物体 m 之间的距离: 由质心位置公式知,质量为 M 的人离质心距离为: 【例 4-5】如图所示,一质量为 的匀质链条,长为 L,手持其上端,下端与桌面接 触。现使链条自静止释放落于桌面,试从下述三种不同的规律出发,计算链条下落 距离时桌 面对链条的作用力: (1)动量规律; (2)质心运动规律; (3)变质量动力学规律; 【解】这是一个连续分布的柔性质点系,可以选择不同的部分作为研究对象,也可以从不同的 角度求解。 方法一,运用动量规律求解。取如图 b 坐标。设 时刻下落至桌面部分的链条长为 ,质量为 ; 至 时间内落到桌面上的链条质量为 ,其速度由 减到 0。选取已下 落至桌面以及 时间内下落至桌面的 段链条为研究对象。由于链条自由下落

败2020+g 和桌面支撑力W的作用,根据质点系动量定理: 20+8-w=0-2 肤的动得艺0”:竖盘 N=32 国正2,代人林啦少=8,家 可见链条下落时对桌面的冲击力为已下落至桌面上链条重量的两倍。 方法二,运用质心运动规律求解。由于整条链条受重力和桌面支撑力的作用,其质心作加速运 动。选取如图c所示的坐标,以整条链条为研究对象。 心之0 2 =血=上 质心速度: 质心加速度: 3 且:t 8 代入上式有: a.(-g)3 根据质心运动定理:N-g=洲a。 N=32g 解得: 方法三,运用变质量动力学规律求解。取下落至桌面部分的链条为研究主体,其质量州逐渐 增加,对如图b坐标,质量流相对主体速度大小:“=U=2g 质量流: 质量流对主体的推力: 主体在其重力、桌面支撑力和质量流对主体的推力作用下保持静止。根据变质量动力学方 程: -g-警=0 同样得到上述结果
段仅受到重力 和桌面支撑力 的作用,根据质点系动量定理: 略去 段重力,得: 因 , ,代入上式,且按题意 ,解得: 。 可见链条下落时对桌面的冲击力为已下落至桌面上链条重量的两倍。 方法二,运用质心运动规律求解。由于整条链条受重力和桌面支撑力的作用,其质心作加速运 动。选取如图 c 所示的坐标,以整条链条为研究对象。 质心位置: 质心速度: 质心加速度: 且: , 代入上式有: 根据质心运动定理: 解得: 方法三,运用变质量动力学规律求解。取下落至桌面部分的链条为研究主体,其质量 逐渐 增加,对如图 b 坐标,质量流相对主体速度大小: 质量流: 质量流对主体的推力: 主体在其重力、桌面支撑力和质量流对主体的推力作用下保持静止。根据变质量动力学方 程: , 同样得到上述结果

号【例46】从地球表面沿与船蛋镜胶角的方向发射一米射体打速度G不 式中M、R分别为地球的质量和半径。若忽略空气阻力和地球自转的影响,试求: (1)抛射体上升的最大高度H和射程的直线距离AD: (2)求飞行时间T. 【解】(1)由于发射速度比较大,飞行高度与地球半径可比较,见图。抛射体在飞行过程 中受到的引力大小和方向都在改变,可以证明其运动轨迹不再是抛物线,而是椭圆。 题图46a 题图46b 抛射体受地球引力作用,对地心的力矩为零,抛射体对地心的角动量守恒。在发射地A和最大 高度B处的角动量满足: (1) 物体只在地球引力作用下运动,系统的机械能守恒: (2) 将GM=g2,=E和(D式代入(2)式,则(2)式简化为: (m'8-2+1=0 r R_1±cos81±cos8 该二次三项式的解为:”m281-co82日 解得: =R(1+cos8) 椭圆的远地点, r2=R(1-cose) 椭圆的近地点。 椭圆的长半轴和短半轴分别为:
【例 4-6】从地球表面沿与铅垂线成 角的方向发射一抛射体初速度 , 式中 M、R 分别为地球的质量和半径。若忽略空气阻力和地球自转的影响,试求: (1)抛射体上升的最大高度 H 和射程的直线距离 AD; (2)求飞行时间 T。 【解】(1)由于发射速度比较大,飞行高度与地球半径可比较,见图 a。抛射体在飞行过程 中受到的引力大小和方向都在改变,可以证明其运动轨迹不再是抛物线,而是椭圆。 抛射体受地球引力作用,对地心的力矩为零,抛射体对地心的角动量守恒。在发射地 A 和最大 高度 B 处的角动量满足: (1) 物体只在地球引力作用下运动,系统的机械能守恒: (2) 将 , 和(1)式代入(2)式,则(2)式简化为: 该二次三项式的解为: , 解得: 椭圆的远地点, 椭圆的近地点。 椭圆的长半轴和短半轴分别为:

4=+5=R b=n =Rsin e (3) 由图b可见,抛射体的发射点和落地点正处在椭圆短半轴的端点上,抛射体飞行的最大高度和 射程的直线距离分别为:H=片-R=Rc0s日 D=2b=2Rsin 6 R 例如沿60°角方向发射,抛射体可达到的最大高度为: (2)由图b所示抛射体的飞行的面积速度: 从发射点到落地点抛射体扫过的面积为半椭圆和一三角形0D面积之和,即: 8=b+2×Rm9Rcos8 +mcos0 由开普勒第二定律得抛射体的飞行时间: “金-+2ae唱 dt + 若日=60°,则飞行时间‘为
(3) 由图 b 可见,抛射体的发射点和落地点正处在椭圆短半轴的端点上,抛射体飞行的最大高度和 射程的直线距离分别为: 例如沿 角方向发射,抛射体可达到的最大高度为: 。 (2)由图 b 所示抛射体的飞行的面积速度: 从发射点到落地点抛射体扫过的面积为半椭圆和一三角形 OAD 面积之和,即: 由开普勒第二定律得抛射体的飞行时间: 若 ,则飞行时间 为