
第8章热力学平衡态 夕一、理想气体状态方程 1、平衡态的概念 系统与外界没有能量交换,系统内部也没有任何形式的能量转换,气体各部分具有相同的温 度和压力,而且温度和压力也不随时间而变化的这种状态叫平衡态。 2、理想气体的状态方程 PV-MRT 这状态方程只适用于平衡态。 式中理想气体普适常数: R=8.31焦耳/摩尔.开=0.082大气压升/摩尔.开=2卡/摩尔.开 3、压力与单位体积内分子数与温度的关系: P=nkT 式中”二工,表示单位体积内的分 =1羽×10焦耳开 称为玻尔兹曼常数。 (式中=602×1020个/摩尔 为阿伏枷德罗常数) 夕三、气体分子运动论 1、宏观量与微观量 气体的温度、压力是大量分子热运动的集体表现,这些描述大量分子集体特征的物理量叫做 宏观量。组成气体的每一分子具有一定的质量、体积、速度、能量等,这些描述单个分子的 物理量叫做微观量。 气体分子运动论就是根据理想气体分子模型用统计的方法研究气体的宏观现象的微观本质, 建立宏观量与微观量的平均值之间关系的理论。 2、理想气体的微观模型。 (一)力学假设: (1)气体分子的线度远小于分子间距。 (2)气体分子可看作为弹性小球,它的运动规律遵守牛顿运动定律。 (3)除碰撞瞬间外,分子间相互作用力可忽略不计
第 8 章 热力学平衡态 一、理想气体状态方程 1、平衡态的概念 系统与外界没有能量交换,系统内部也没有任何形式的能量转换,气体各部分具有相同的温 度和压力,而且温度和压力也不随时间而变化的这种状态叫平衡态。 2、理想气体的状态方程 这状态方程只适用于平衡态。 式中理想气体普适常数: 3、压力与单位体积内分子数与温度的关系: 式中 ,表示单位体积内的分子数, ,称为玻尔兹曼常数。 (式中 ,为阿伏枷德罗常数) 二、气体分子运动论 1、宏观量与微观量 气体的温度、压力是大量分子热运动的集体表现,这些描述大量分子集体特征的物理量叫做 宏观量。组成气体的每一分子具有一定的质量、体积、速度、能量等,这些描述单个分子的 物理量叫做微观量。 气体分子运动论就是根据理想气体分子模型用统计的方法研究气体的宏观现象的微观本质, 建立宏观量与微观量的平均值之间关系的理论。 2、理想气体的微观模型。 (一)力学假设: (1)气体分子的线度远小于分子间距。 (2)气体分子可看作为弹性小球,它的运动规律遵守牛顿运动定律。 (3)除碰撞瞬间外,分子间相互作用力可忽略不计

(二)平衡态时的统计假设: (1)分子向各个方向运动的机会均等。 (2)分子速度在各个方向上分量的各种平均值也相等。 交 2==u 3、理想气体的压力公式 P=M 4、气体分子的平均平动动能与温度的关系 8=7 它揭示了宏观量温度是气体分子无规则运动量度的物理本质。 5、能量均分原理 任一自由度上的平均能量都是2 ,这叫能量均分原理 ‘表示平动自由度,”表示其转动自由度,S表示其振动自由度,分子的总自由度 1=t+r+28 (1)单原子分子:i=3 百-号7 (2)在温度不太高的条件下,双原子分子可看成刚性分子,振动自由度S取零得:1=5 刚性双原子分子 6=57=37 (3)刚性多原子分子 2 6、理想气体的内能 理想气体的内能是系统状态的单值函数。 夕三、麦克斯韦速率分布 1、麦克斯韦速率分布函数的意义 f)-Nao 表示单位速奉区间内的分子数占总分子数的比奉
(二)平衡态时的统计假设: (1)分子向各个方向运动的机会均等。 (2)分子速度在各个方向上分量的各种平均值也相等。 有 3、理想气体的压力公式 4、气体分子的平均平动动能与温度的关系 它揭示了宏观量温度是气体分子无规则运动量度的物理本质。 5、能量均分原理 任一自由度上的平均能量都是 ,这叫能量均分原理。 表示平动自由度, 表示其转动自由度,S 表示其振动自由度,分子的总自由度: (1)单原子分子: (2)在温度不太高的条件下,双原子分子可看成刚性分子,振动自由度 S 取零得: 刚性双原子分子 (3)刚性多原子分子 6、理想气体的内能 理想气体的内能是系统状态的单值函数。 三、麦克斯韦速率分布 1、麦克斯韦速率分布函数的意义 表示单位速率区间内的分子数占总分子数的比率
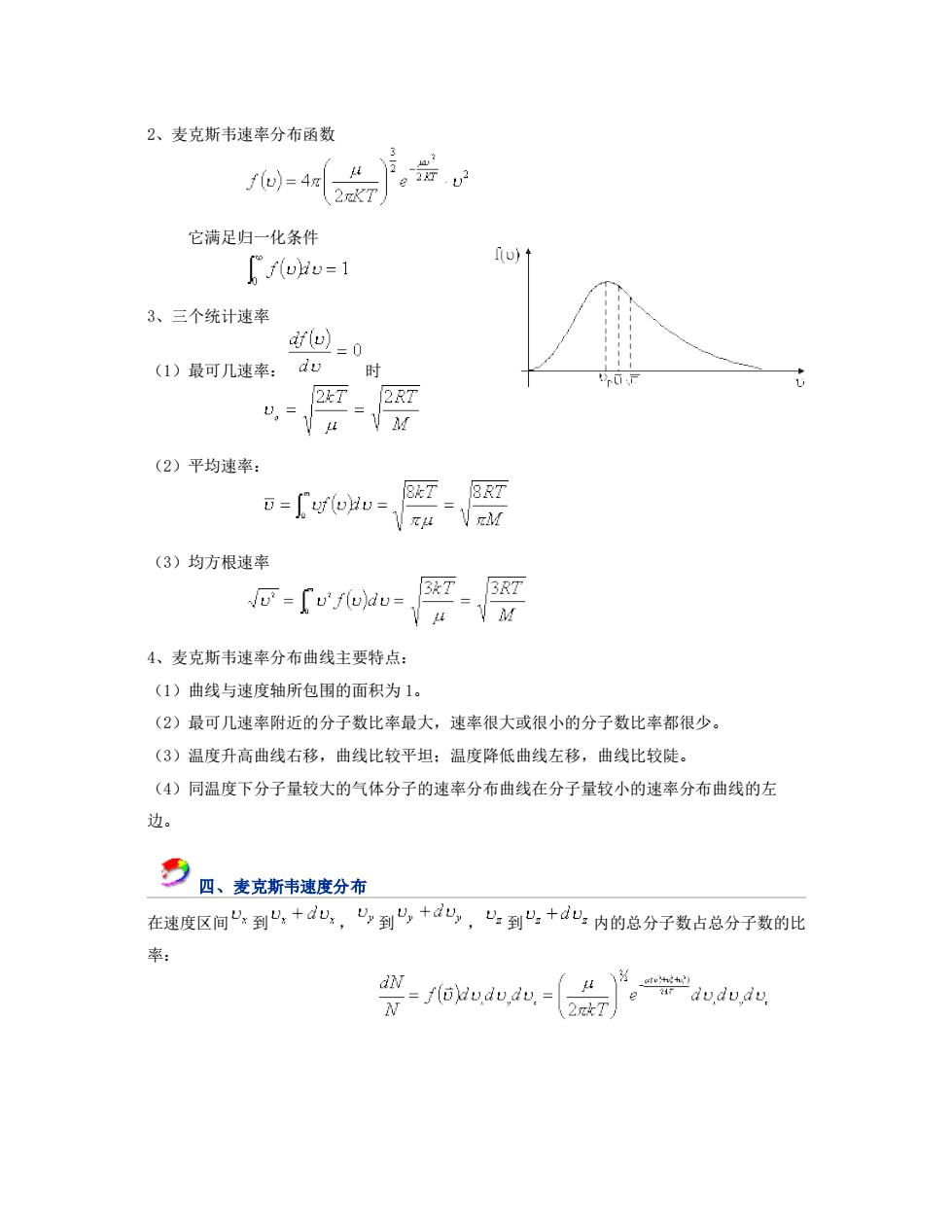
2、麦克斯韦速率分布函数 f⊙)=4x 它满足归一化条件 f(o)t [f(oriv=1 3、三个统计速率 回-0 (1)最可几速率:du时 (2)平均速率: =[ufou=. V (3)均方根速率 o=〔'f(u)dv= 4、麦克斯韦速率分布曲线主要特点: (1)曲线与速度轴所包围的面积为1。 (2)最可几速率附近的分子数比率最大,速率很大或很小的分子数比率都很少。 (3)温度升高曲线右移,曲线比较平坦:温度降低曲线左移,曲线比较陡。 (4)同温度下分子量较大的气体分子的速率分布曲线在分子量较小的速率分布曲线的左 边。 夕日、类克斯率遗度分有 在速度区间“:到4,+d心,凸到+d,“:到兴,+d心:内的总分子数占总分子数的肚 @yw.du.iw- 27 。dwdD,dy
2、麦克斯韦速率分布函数 它满足归一化条件 3、三个统计速率 (1)最可几速率: 时 (2)平均速率: (3)均方根速率 4、麦克斯韦速率分布曲线主要特点: (1)曲线与速度轴所包围的面积为 1。 (2)最可几速率附近的分子数比率最大,速率很大或很小的分子数比率都很少。 (3)温度升高曲线右移,曲线比较平坦;温度降低曲线左移,曲线比较陡。 (4)同温度下分子量较大的气体分子的速率分布曲线在分子量较小的速率分布曲线的左 边。 四、麦克斯韦速度分布 在速度区间 到 , 到 , 到 内的总分子数占总分子数的比 率:

分子对器壁单位面积上碰撞的频率: 夕五、玻耳滋更统计分布 dN=Cedvdv,dv,dxdydz 式中宁转为破西装曼因下,共中品和二,末示分于动能和分于在外场中的势 能。重力场中粒子按高度分布: 六大、知识体系方框图 在 统计促没 生力公式 长,当,逃度牙亦补 品及公 支一浊辛分介律 座南南
分子对器壁单位面积上碰撞的频率: 五、玻耳兹曼统计分布 式中 称为玻耳兹曼因子,其中 和 表示分子动能和分子在外场中的势 能。重力场中粒子按高度分布: 六、知识体系方框图

第8章热力学平衡态 号【例8-1】大量拉子=72×10”个,它们的速度分布函数图象如愿图8-1a所示,试 求: (1)速度小于30m/s的分子数约为多少? (2)速度处在9m/s到01m/s之间的分子数约为多少? (3)所有个粒子的平均速度为多少2 (4)速度大于50m/8的那些分子的平均速度为多少? Hu) 【解】(1)由归一化条件可知速度分布函数与速度坐标所包围的面积应为1,即: 3×0+60-30u+020-60h-1 1 求得常数: a275 图b中所示三角形1的面积表示速度小于30ms的分子数占总分子数的比率,所以速度小于 30/s的分子数为: ==30a =72×10分×30×=14410 2 个 (2)与(1)同理,速度处于99m8到101以/8之间的分子数占总分子数的比率由图b中阴 影面积△S表示,在此速度之间的分子数: Aw=△-%×a×du=72100×号×01-9=64×10 个 (3)所有粒子的平均速度: dofu-wte 120 30 50 上述方法首先要找出(四函数表达式,再要积分,运算较烦。若理解一下函数图象的积分式
第 8 章 热力学平衡态 【例 8-1】大量粒子 个,它们的速度分布函数图象如题图 8-1a 所示,试 求: (1)速度小于 的分子数约为多少? (2)速度处在 到 之间的分子数约为多少? (3)所有 个粒子的平均速度为多少? (4)速度大于 的那些分子的平均速度为多少? 【解】(1)由归一化条件可知速度分布函数与速度坐标所包围的面积应为 1,即: 求得常数: 图 b 中所示三角形 的面积表示速度小于 的分子数占总分子数的比率,所以速度小于 的分子数为: 个 (2)与(1)同理,速度处于 到 之间的分子数占总分子数的比率由图 b 中阴 影面积 表示,在此速度之间的分子数: 个 (3)所有粒子的平均速度: 上述方法首先要找出 函数表达式,再要积分,运算较烦。若理解一下函数图象的积分式

通义,不妨将速度坐标轴看作x轴,(四看作'轴,上述积分式可写成: ∫wa=∫xs 式中S是一窄条阴影面积,又总面积S为1,所以此积分表示的是总面积的质心的x坐标即 不。,由此可通过求速度分布图形的“质心”位置来求得平均速度。参图b可得: D=x1+xx8+x83 =2×30×2×30xa+3B0+6060-30a 3 2 +0+020-602020-60 1 =300+1350+2400k=4050×75=54m16 (4)速度大于那些分子的平均速度的一般解法: 130 v dN wof(u)du 2-0n =0 dN =80w/s 而通过(3)中介绍的“质心”法解,直接可得: 5=60+30120-60=80w1s 夕【例8-2】理想气体分子沿方向的速度分布函数: ,试据此 推导压强公式P=T.(已知: dx=) 【解】设x方向垂直于容器壁。单位面积内速度处于“:到“,十:速度分量的分子数为 u,)u,在4时间内与A器壁上碰撞的次数为矿包,d0,小巴应△ ,每一次器壁 给个分于的量=2,压”公用制分形式衣示 p=2uv,n v,f(v,)dv,=2mvif(v,)dv, 0 =2w小oe尚u 令,上式可写成
涵义,不妨将速度坐标轴看作 轴, 看作 轴,上述积分式可写成: 式中 是一窄条阴影面积,又总面积 S 为 1,所以此积分表示的是总面积的质心的 坐标即 ,由此可通过求速度分布图形的“质心”位置来求得平均速度。参图 b 可得: (4)速度大于那些分子的平均速度的一般解法: = 而通过(3)中介绍的“质心”法解,直接可得: 【例 8-2】理想气体分子沿 方向的速度分布函数: ,试据此 推导压强公式 。(已知: ) 【解】设 方向垂直于容器壁。单位面积内速度处于 到 速度分量的分子数为 ,在 时间内与 器壁上碰撞的次数为 ,每一次器壁 给一个分子的冲量 ,压强 ,用积分形式表示: 令 ,上式可写成:
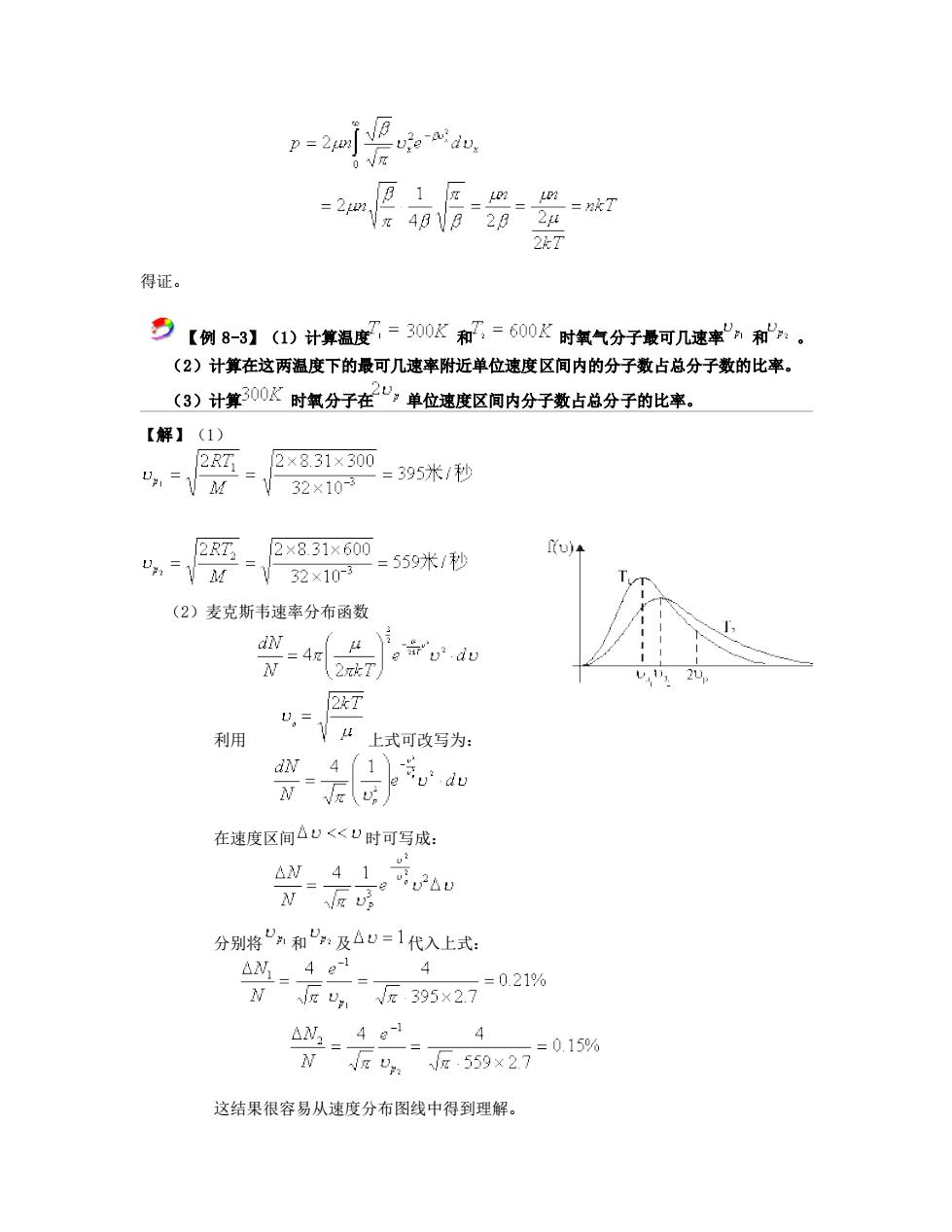
22T 得证。 乡【例8-3】(1)计算温度=300K和了=600K时氧气分子最可几速率n和。 (2)计算在这两温度下的最可几速率附近单位速度区间内的分子数占总分子数的比率。 (3)计算300K时氧分子在“,单位速度区间内分子数占总分子的比率。 【解】(1) 2RT 2×8.31×300 =395米/秒 V32×103 2R, 2×8.31×600 “:=M =V32×10 =559米1秒 ) (2)麦克斯韦速率分布函数 2k7 利用 心,江上式可改写为: 器,u 在速度区间△U<U时可写成: 兴好ae U 分别将和:及△v=1代入上式: 4 N反反5×27=021% 4 √π, 反59x27-015% 这结果很容易从速度分布图线中得到理解
得证。 【例 8-3】(1)计算温度 和 时氧气分子最可几速率 和 。 (2)计算在这两温度下的最可几速率附近单位速度区间内的分子数占总分子数的比率。 (3)计算 时氧分子在 单位速度区间内分子数占总分子的比率。 【解】(1) (2)麦克斯韦速率分布函数 利用 上式可改写为: 在速度区间 时可写成: 分别将 和 及 代入上式: 这结果很容易从速度分布图线中得到理解

A2.41号a-41e4wg如 (3)N反g 式中△u=1,所以: 16 a2=东9325xg42x10=0042% 这表明分子速率随偏离·增大,单位速度区间内的分子比率迅速减少。 ui du 【例8】试格质量为的单原子理短气你速率分布员最:2庆 改写 成拔动能0 分布的函数形式(©d8,然后求出其最可几动能及平均动能。 =医=,将此关 as ,将它微分d8=U,分别可得: 系代入速率分布函数: 、t3÷.2E2—=21eEde 424sV元kT 由此得单原子理想气体按动能分布函数: f(e-2(。立E n kT df(6)=0 最可几动能的条件:de 290 得.2e司元@+ 食里限限限明下,可速来对皮的动能如户 并不是最可几动能。 这里因为分布函数不同,同时所考虑的速度间隔禳?搜?琸?田?-一 ??dv和能量间隔de也不同
(3) 式中 ,所以: 这表明分子速率随偏离 增大,单位速度区间内的分子比率迅速减少。 【例 8-4】试将质量为 的单原子理想气体速率分布函数 改写 成按动能 分布的函数形式 ,然后求出其最可几动能及平均动能。 【解】由 ,将它微分 ,分别可得: , ,将此关 系代入速率分布函数: 由此得单原子理想气体按动能分布函数: 最可几动能的条件: 得: 解得: 这里顺便说明一下,最可几速率对应的动能 = 并不是最可几动能。 这里因为分布函数不同,同时所考虑的速度间隔欀?獀?琸?田??? ????? 和能量间隔 也不同

i-Jd(o)de-Je2(oilads-3kT 平均动能: 这里的具体体积分过程是较麻烦的,这里从略了。 号【例8-6】一容餐体积为”,一导热隔板把它分成相等的两半,开始时左边座有压强 为品的理想气体,右边为真空。在隔板上有一面积为S的小洞,求打开小洞后左右两边压强 和3与时呼的关系(尼知华位时间与器壁单位面积相堂的分于黄为可)。 55 【解】设某一时刻左边有N个分子,右边有%一W个分子。在止时间内左边分子数的增 北+,业 =(4-20 因%7: kT ,将上式两边乘以口 .中- 分离变量并积分: h6-2p 6-25-2p 2
平均动能: 这里的具体体积分过程是较麻烦的,这里从略了。 【例 8-5】一容器体积为 ,一导热隔板把它分成相等的两半,开始时左边盛有压强 为 的理想气体,右边为真空。在隔板上有一面积为 S 的小洞,求打开小洞后左右两边压强 和 与时间 的关系(已知单位时间与器壁单位面积相撞的分子数为 )。 【解】设某一时刻左边有 N 个分子,右边有 个分子。在 时间内左边分子数的增 量: 因为 ,将上式两边乘以 得: 即: 分离变量并积分: 得:

上式是对左边容器计算所得,所以应写成 kT 由于两边分子的总和 从+从=从等式两边各乘以下后可知月+月=乃,所以 右边容器压强与时间关系为: R=R-P=91-e9
上式是对左边容器计算所得,所以应写成 由于两边分子的总和 等式两边各乘以 后可知 ,所以 右边容器压强与时间关系为: