
第2章质点动力学 一、质点 是物体的理想模型。它只有质量而没有大小。平动物体可作为质点运动来处理,或物体的形 状大小对物体运动状态的影响可忽略不计是也可近似为质点。 9三、力: 是物体间的相互作用。分为接触作用与场作用。在经典力学中,场作用主要为万有引力(重 力),接触作用主要为弹性力与摩擦力。 1、弹性力:F=- (x为形变量) 2、摩擦力:摩擦力的方向永远与相对运动方向(或趋势)相反。 固体间的静摩擦力:了=4W (最大值) 固体间的滑动摩擦力:大=4,N 3、流体阻力:了=-bv或了=-cu =GMin 4、万有引力: GMi 特例:在地球引力场中,在地球表面附近: F-R-ME 式中R为地球半径,M为地球质量。 在地球上方(”较大), 在地球内部(<R), P=州8R 号三、债性参考系中的力学提律牛顿三定排 牛顿第一定律:户=0时,=恒矢量。牛顿第一定律阐明了惯性与力的概念,定义了惯 性系。 牛顿第二定律: 方=dw) 普遍形式: d 经典形式: (m为恒量) 牛顿第三定律:月。=-瓦
第 2 章 质点动力学 一、质点: 是物体的理想模型。它只有质量而没有大小。平动物体可作为质点运动来处理,或物体的形 状大小对物体运动状态的影响可忽略不计是也可近似为质点。 二、力: 是物体间的相互作用。分为接触作用与场作用。在经典力学中,场作用主要为万有引力(重 力),接触作用主要为弹性力与摩擦力。 1、弹性力: ( 为形变量) 2、摩擦力:摩擦力的方向永远与相对运动方向(或趋势)相反。 固体间的静摩擦力: (最大值) 固体间的滑动摩擦力: 3、流体阻力: 或 。 4、万有引力: 特例:在地球引力场中,在地球表面附近: 。 式中 R 为地球半径,M 为地球质量。 在地球上方( 较大), 。 在地球内部( ), 。 三、惯性参考系中的力学规律 牛顿三定律 牛顿第一定律: 时, 。牛顿第一定律阐明了惯性与力的概念,定义了惯 性系。 牛顿第二定律: 普遍形式: ; 经典形式: ( 为恒量) 牛顿第三定律:

牛顿运动定律是物体低速运动(U<C)时所遵循的动力学基本规律,是经典力学的基 础。 乡 四、非惯性参考系中的力学规律 1、惯性力: 京=-ma-a)- ”→平移加速系疗=一d, →匀速转动系豆=-mm节,(@=0) 惯性力没有施力物体,因此它也不存在反作用力。但惯性力同样能改变物体相对于参考系的 运动状态,这体现了惯性力就是参考系的加速度效应。 2、引入惯性力后,非惯性系中力学规律:F+云=m 号五、泉桥动力学日愚的主要步 恒力作用下的连接体约束运动:选取研究对象,分析运动趋势,画出隔离体示力图,列出分 量式的运动方程。 变力作用下的单质点运动:分析力函数,选取坐标系,列运动方程,用积分法求解
牛顿运动定律是物体低速运动( )时所遵循的动力学基本规律,是经典力学的基 础。 四、非惯性参考系中的力学规律 1、惯性力: 惯性力没有施力物体,因此它也不存在反作用力。但惯性力同样能改变物体相对于参考系的 运动状态,这体现了惯性力就是参考系的加速度效应。 2、引入惯性力后,非惯性系中力学规律: 五、求解动力学问题的主要步骤 恒力作用下的连接体约束运动:选取研究对象,分析运动趋势,画出隔离体示力图,列出分 量式的运动方程。 变力作用下的单质点运动:分析力函数,选取坐标系,列运动方程,用积分法求解

第2章质点动力学 夕二、解题示例 【例2-1】如题图2-1a所示一倾角为的斜面放在水平面上,斜面上放一木块,两者 间摩擦系数为4<g⊙)。为使木块相对斜面静止,求斜面加速度的范围。 m --ra mg 题21b y 题21a 题21c 【解】方法一我们如b图取坐标,并假设物体有下滑趋势,根据受力图可列出动力学方 2Nsm-fcos8=ma Ncos日+fsm日-g=0 这样两个方程两个未知数,可解,但解的过程较繁。若将坐标轴分别沿斜面和斜面垂直方法上 取,使得一个未知力与一个坐标轴垂直,使得在一个方向上的方程中只出现一个未知力,这样 一个方程就能独立地解出一个未知力来了。如图c所示可列出如下牛顿动力学方程: x方向 mg sin e-f=macose y方向 N-gcos日=masm日 由此解得 f=wgsm日-macos日 N=mg cos e+masine 由相对静止条件要求 -W≤f≤國 可解得加速度a的范围为:
第 2 章 质点动力学 二、解题示例 【例 2-1】如题图 2-1a 所示一倾角为 的斜面放在水平面上,斜面上放一木块,两者 间摩擦系数为 。为使木块相对斜面静止,求斜面加速度 的范围。 【解】方法一 我们如 b 图取坐标,并假设物体有下滑趋势,根据受力图可列出动力学方 程: 这样两个方程两个未知数,可解,但解的过程较繁。若将坐标轴分别沿斜面和斜面垂直方法上 取,使得一个未知力与一个坐标轴垂直,使得在一个方向上的方程中只出现一个未知力,这样 一个方程就能独立地解出一个未知力来了。如图 c 所示可列出如下牛顿动力学方程: x 方向 y 方向 由此解得 由相对静止条件要求 可解得加速度 的范围为:
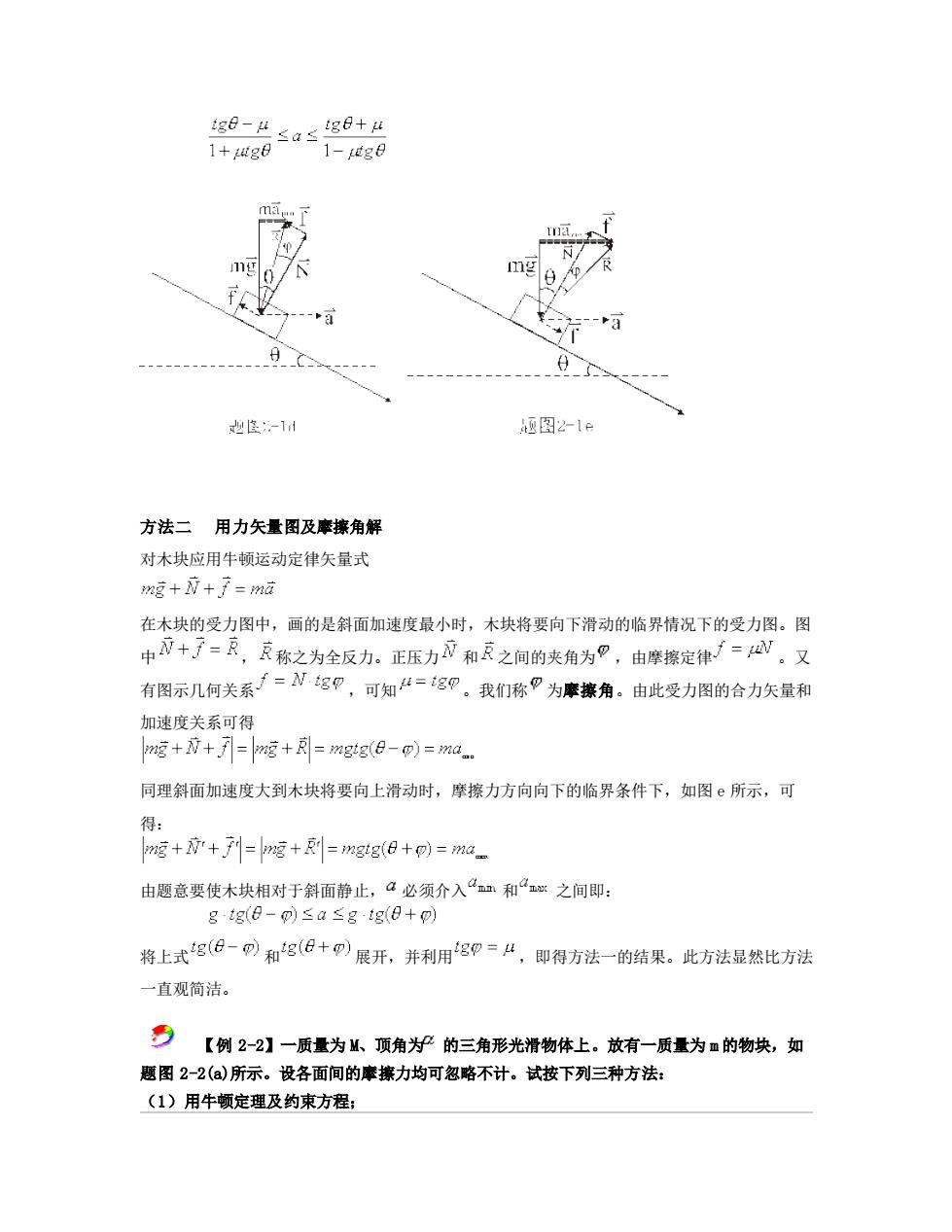
tg8-4 1+g8 sas ige+u 1-g日 ma 起退女1d @图21e 方法二用力矢量图及摩擦角解 对木块应用牛顿运动定律矢量式 w落+衣+了=m这 在木块的受力图中,画的是斜面加速度最小时,木块将要向下滑动的临界情况下的受力图。图 中+了=瓦,反称之为全反力.正压力衣和反之间的夹角为巴,由摩擦定律=V。又 有图示几何关系了=NgP,可知“=g9。我们称P为摩擦角。由此受力图的合力矢量和 加速度关系可得 g++=馆+=mgge-)=ma. 同理斜面加速度大到木块将要向上滑动时,摩擦力方向向下的临界条件下,如图©所示,可 得: 9馆+7r+升=g+利=mgg(6+)=a 由题意要使木块相对于斜面静止,a必须介入a和之间即: gge-网≤a≤gtg(e+ 将上式38-网和3(8+网展开,并利用89=“,即得方法一的结果。此方法显然比方法 一直观简洁。 号【倒2-2】一质量为以、顶角为的三角形光滑物体上。放有一质量为■的物块,如 题图2-2()所示。设各面间的率擦力均可忽略不计。试按下列三种方法: (1)用牛顿定理及约束方程:
方法二 用力矢量图及摩擦角解 对木块应用牛顿运动定律矢量式 在木块的受力图中,画的是斜面加速度最小时,木块将要向下滑动的临界情况下的受力图。图 中 , 称之为全反力。正压力 和 之间的夹角为 ,由摩擦定律 。又 有图示几何关系 ,可知 。我们称 为摩擦角。由此受力图的合力矢量和 加速度关系可得 同理斜面加速度大到木块将要向上滑动时,摩擦力方向向下的临界条件下,如图 e 所示,可 得: 由题意要使木块相对于斜面静止, 必须介入 和 之间即: 将上式 和 展开,并利用 ,即得方法一的结果。此方法显然比方法 一直观简洁。 【例 2-2】一质量为 M、顶角为 的三角形光滑物体上。放有一质量为 m 的物块,如 题图 2-2(a)所示。设各面间的摩擦力均可忽略不计。试按下列三种方法: (1)用牛顿定理及约束方程;
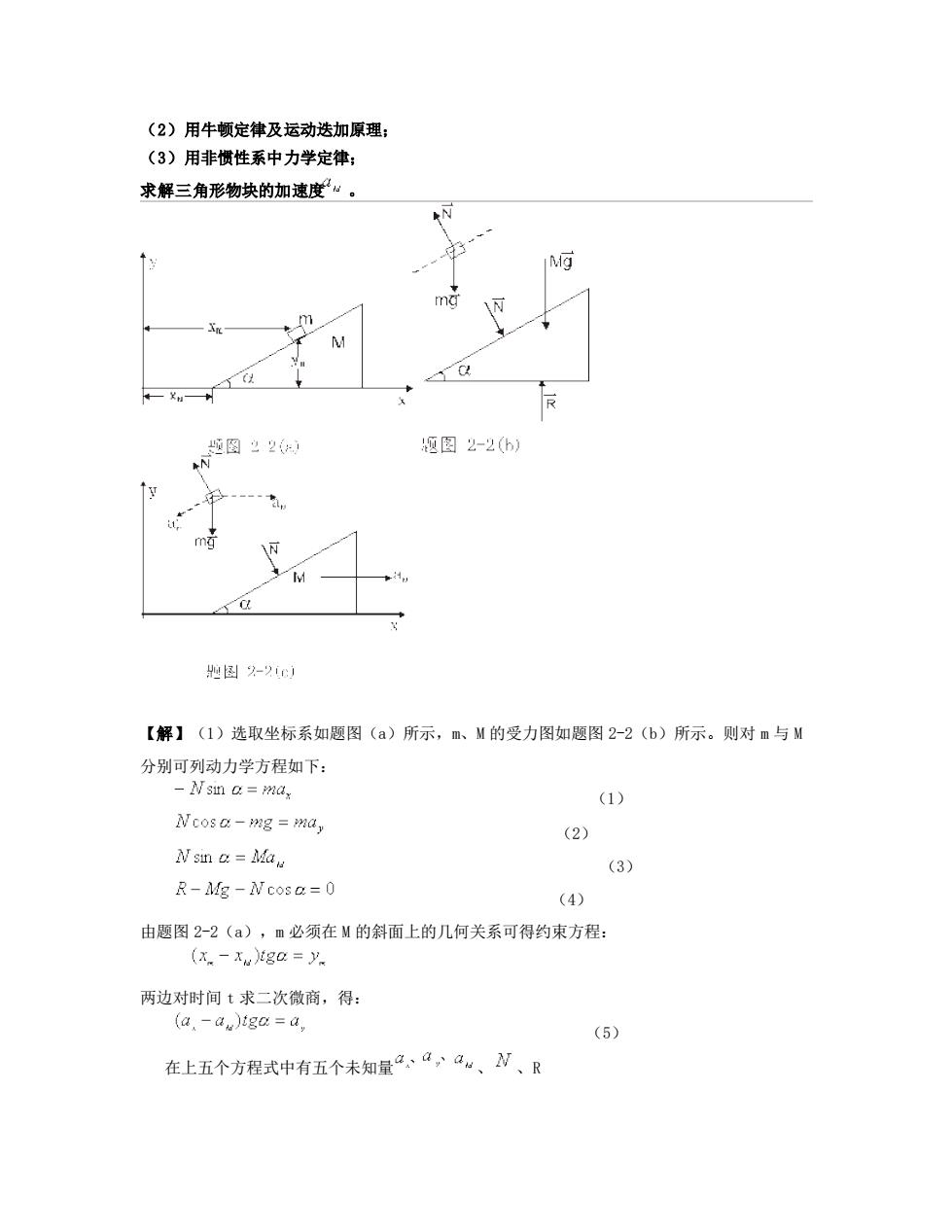
(2)用牛顿定律及运动迭加原理: (3)用非惯性系中力学定律; 求解三角形物块的加速度“。 N +N型图2 题图2-2(6) 担图-cd 【解】(1)选取坐标系如题图()所示,m、M的受力图如题图2-2(b)所示。则对m与M 分别可列动力学方程如下: -N sin a=ma (1) Ncosa-mg=mdy (2) Nsim a=May (3) R-Mg-Ncosa=0 (4) 由题图2-2(a),m必须在M的斜面上的几何关系可得约束方程: (x.-xuiga=y. 两边对时间t求二次微商,得 (a.-d)iga=a, (5) 在上五个方程式中有五个未知量4,“,a。、N、R
(2)用牛顿定律及运动迭加原理; (3)用非惯性系中力学定律; 求解三角形物块的加速度 。 【解】(1)选取坐标系如题图(a)所示,m、M 的受力图如题图 2-2(b)所示。则对 m 与 M 分别可列动力学方程如下: (1) (2) (3) (4) 由题图 2-2(a),m 必须在 M 的斜面上的几何关系可得约束方程: 两边对时间 t 求二次微商,得: (5) 在上五个方程式中有五个未知量 、 、R
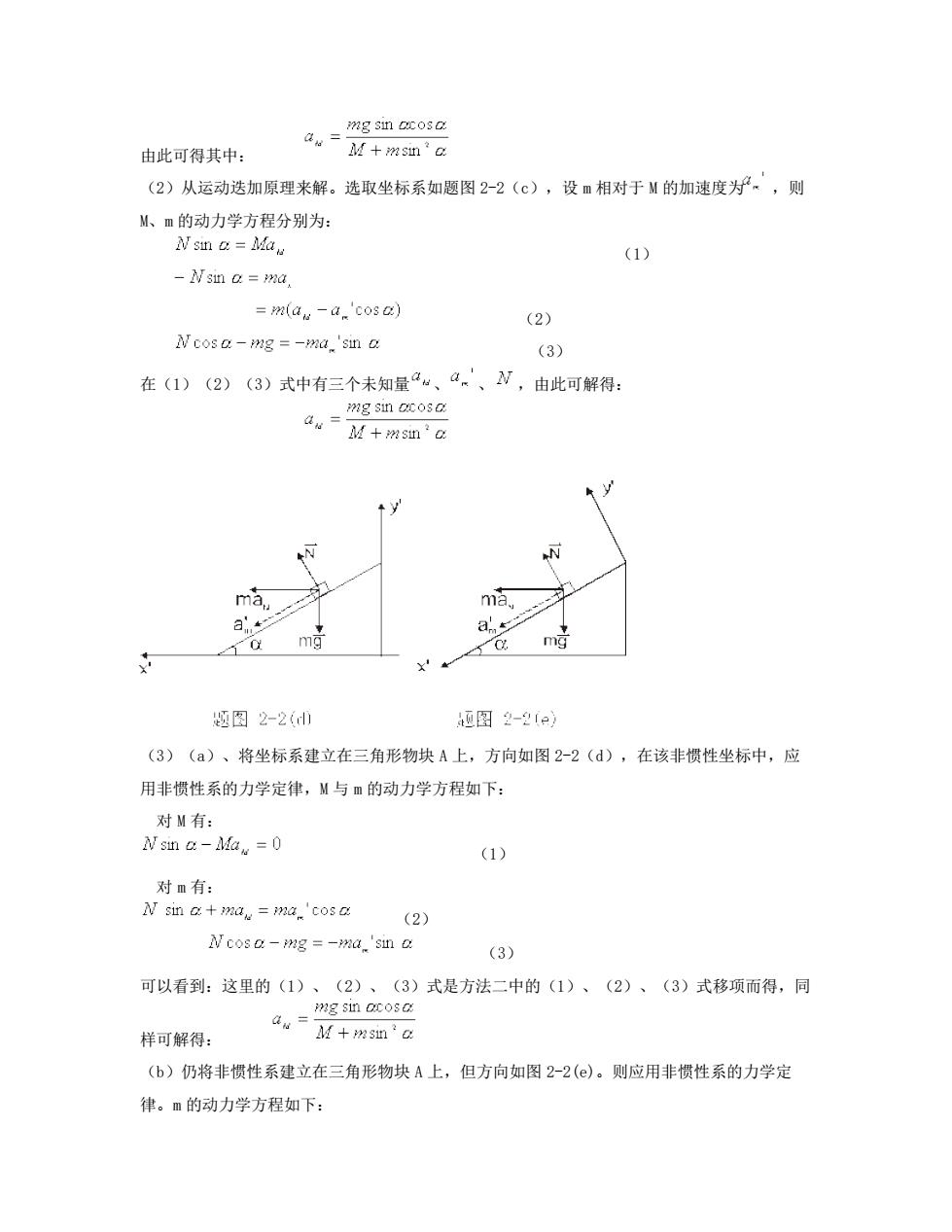
mg sin ocosa 由此可得其中: au=+msn'a (2)从运动迭加原理来解。选取坐标系如题图2-2(),设m相对于M的加速度为.',则 M、m的动力学方程分别为: (1) -Nsmn a ma. =m(ay-a'cosa) (2) Ncosa-mg =-ma.'sin a (3) 在(1)(2)(3)式中有三个未知量a“、a、、N,由此可解得: mg sin ocosa au=M+msm'a m话 ma 1 0 X 题图2-20 0图2-2e) (3)(a)、将坐标系建立在三角形物块A上,方向如图2-2(d),在该非惯性坐标中,应 用非惯性系的力学定律,M与m的动力学方程如下: 对M有: Nsin a-Ma =0 (1) 对m有: N sin a+may ma'cosa (2) Ncosa-mg =-ma'sin a (3) 可以看到:这里的(1)、(2)、(3)式是方法二中的(1)、(2)、(3)式移项而得,同 样可解得: (b)仍将非惯性系建立在三角形物块A上,但方向如图2-2()。则应用非惯性系的力学定 律。m的动力学方程如下:
由此可得其中: (2)从运动迭加原理来解。选取坐标系如题图 2-2(c),设 m 相对于 M 的加速度为 ,则 M、m 的动力学方程分别为: (1) (2) (3) 在(1)(2)(3)式中有三个未知量 、 、 ,由此可解得: (3)(a)、将坐标系建立在三角形物块 A 上,方向如图 2-2(d),在该非惯性坐标中,应 用非惯性系的力学定律,M 与 m 的动力学方程如下: 对 M 有: (1) 对 m 有: (2) (3) 可以看到:这里的(1)、(2)、(3)式是方法二中的(1)、(2)、(3)式移项而得,同 样可解得: (b)仍将非惯性系建立在三角形物块 A 上,但方向如图 2-2(e)。则应用非惯性系的力学定 律。m 的动力学方程如下:

对m有: ma cos a+mg sin a=md' (1) N+ma sin a-mg cosa=0 (2) 对M仍有:Nsm&-Ma,=0 (3) 在(2)、(3)式中仅含有N、“两个未知量,由此可解得: mg sin acosa aw= M+sn 显然,按图(b)的坐标方向选取仅需要两个方程联立求解。比按()选取的坐标方向来求解 要容易得多。所以坐标方向选取的原则是使未知数尽量具有一个方向的分量。如按(b)的坐 标方向,“、、N都分别只具有不'与'方向的分量。这样可避免解联立方程使问题简化。从本 例看来用非惯性力学定律来解是比较方便的,但在很多情况下还是应具体问题分析,不能一概 而论那种方法最为简单。 夕【例2-3】图柱形容器内装有一定量的液体,若它们一起绕圆柱轴以角速度匀速转 动,试问稳定旋转时液面的形状如何? 【解】方法一设液体稳定旋转时液面是绕2轴的某种旋转曲面,它与2平面的交线如图 4所示。液面上任一质元△”作圆周运动,其余部分液体对该质元的作用力W垂直与液面。 由图a中,△”的受力图对△”的y方向和z方向分别列出牛顿动力学方程: Nsma=△xm2y Ncosa-△mg=0 ga=心y 解得: g 由几何关系可知,△洲处切线的斜率 dy g 2 2-202 2 积分可得 液体旋转时,可见在YO平面上的液面是抛物线。若考虑到质元△”离开z轴的距离 r=vx'+y' 2-2=(x+y ,则整个液面呈旋转抛物面,它的方程为: 2g
对 m 有: (1) (2) 对 M 仍有: (3) 在(2)、(3)式中仅含有 N、 两个未知量,由此可解得: 显然,按图(b)的坐标方向选取仅需要两个方程联立求解。比按(a)选取的坐标方向来求解 要容易得多。所以坐标方向选取的原则是使未知数尽量具有一个方向的分量。如按(b)的坐 标方向, 、N 都分别只具有 与 方向的分量。这样可避免解联立方程使问题简化。从本 例看来用非惯性力学定律来解是比较方便的,但在很多情况下还是应具体问题分析,不能一概 而论那种方法最为简单。 【例 2-3】圆柱形容器内装有一定量的液体,若它们一起绕圆柱轴以角速度 匀速转 动,试问稳定旋转时液面的形状如何? 【解】方法一 设液体稳定旋转时液面是绕 轴的某种旋转曲面,它与 平面的交线如图 所示。液面上任一质元 作圆周运动,其余部分液体对该质元的作用力 垂直与液面。 由图 a 中, 的受力图对 的 y 方向和 z 方向分别列出牛顿动力学方程: , 解得: 。 由几何关系可知, 处切线的斜率 ; 积分可得 。 液体旋转时,可见在 YOZ 平面上的液面是抛物线。若考虑到质元 离开 z 轴的距离 ,则整个液面呈旋转抛物面,它的方程为:

恶2ǎ 题2补 方法二在液体内部取一平行于》轴的短质元,如图b所示。质元两端离液面的高度不同, 分别为2和2十边。质元作圆周运动时的向心力是该质元两侧受到的液体压力差所提供的。设 液体的密度为P,该质源的动力学方程为:PAs-3仁+也)As=一m心c沙 即 由此积分同样得上述结果。 号【例2-4】质囊”,以初速上菊一物体,设它所受的空气阻力与速度成正比,即 了=一”,试求该物体的运动规律
方法二 在液体内部取一平行于 轴的短质元,如图 b 所示。质元两端离液面的高度不同, 分别为 和 。质元作圆周运动时的向心力是该质元两侧受到的液体压力差所提供的。设 液体的密度为 ,该质源的动力学方程为: 即 由此积分同样得上述结果。 【例 2-4】质量 ,以初速 上抛一物体,设它所受的空气阻力与速度成正比,即 ,试求该物体的运动规律
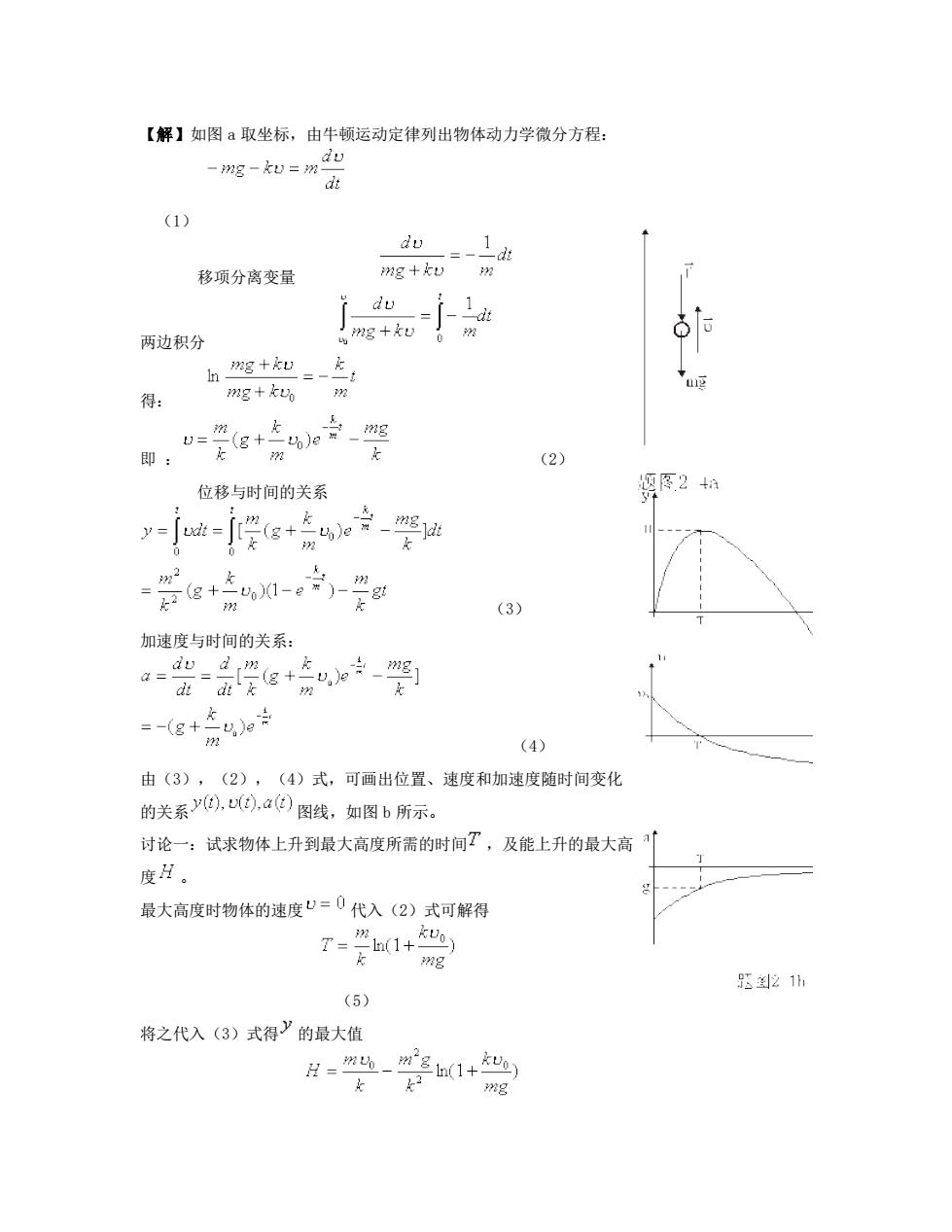
【解】如图a取坐标,由牛顿运动定律列出物体动力学微分方程: -mg-=m20 (1) du 移项分离变量 mg+kv du 两边积分 g+机 u 得: 即: (2) 位移与时间的关系 顺图2+n -=学g+东宁坚 (3) 加速度与时间的关系: (4) 由(3),(2),(4)式,可画出位置、速度和加速度随时间变化 的关系0.0,a心图线,如图b所示. 讨论一:试求物体上升到最大高度所需的时间T,及能上升的最大高 1 度H。 最大高度时物体的速度”=0代入(2)式可解得 7-1+ g 器21 (5) 将之代入(3)式得》的最大值
【解】如图 a 取坐标,由牛顿运动定律列出物体动力学微分方程: (1) 移项分离变量 两边积分 得: 即 : (2) 位移与时间的关系 (3) 加速度与时间的关系: (4) 由(3),(2),(4)式,可画出位置、速度和加速度随时间变化 的关系 图线,如图 b 所示。 讨论一:试求物体上升到最大高度所需的时间 ,及能上升的最大高 度 。 最大高度时物体的速度 代入(2)式可解得 (5) 将之代入(3)式得 的最大值

(6) k<1 讨论二:若空气阻力比其重力小得多,即州g 的条件下,再求 物体上升高度20和时间20。 由于当x<1时h(1+)兰x由(5)式 这正好与不计空气阻力情况相同。 品-2-要1+赠 g mte m'g keg=0 由(6)式 这与事实不,应注意到<1时1++ 23 应取到二阶无穷小项,则: 风学学格尝器 这仍于不计空气阻力条件下上抛物上升最大高度相同
(6) 讨论二:若空气阻力比其重力小得多,即 的条件下,再求 物体上升高度 和时间 。 由于当 时 由(5)式 这正好与不计空气阻力情况相同。 由(6)式 这与事实不符,应注意到 时 应取到二阶无穷小项,则: 这仍于不计空气阻力条件下上抛物上升最大高度相同