
第6章振动力学基础 夕一、产生谐振动的动力学条件 物体受到的合外力或合外力矩为零的位置,我们称之为平衡位置。当物体偏离平衡位置时, 物体受到与位移成正比与位移方向相反的恢复力(F=一《x),或受到与角位移成正比与 角位移方向相反的恢复力矩(过=℃日)作用时物体将作谐振动。 c /00000000 - 图6-1 62 1、弹簧振子(图6-1) d 这微分方程的解为: x=Acos(at+) 式中贸频 由此可得振动周 T= 2、复摆(物理摆) 2 =-g6日 式中b为支点到质心的距离,也常用·表示。 这微分方程的解为:8=8c0s@+ 222b T=2m J ,由此可得振动周期 3、其他类型简谐振动的一般求解步骤: (1)选取合适的坐标,找出平衡位置。 (2)写出在平衡位置处物体所受各力的平衡条件,(在此较简单的情况下这一步可省
第 6 章 振动力学基础 一、产生谐振动的动力学条件 物体受到的合外力或合外力矩为零的位置,我们称之为平衡位置。当物体偏离平衡位置时, 物体受到与位移成正比与位移方向相反的恢复力( ),或受到与角位移成正比与 角位移方向相反的恢复力矩( )作用时物体将作谐振动。 1、弹簧振子(图 6-1) 这微分方程的解为: 式中圆频率 由此可得振动周期 2、复摆(物理摆) 式中 b 为支点到质心的距离,也常用 表示。 这微分方程的解为: 式中圆频率 ,由此可得振动周期 3、其他类型简谐振动的一般求解步骤: (1)选取合适的坐标,找出平衡位置。 (2)写出在平衡位置处物体所受各力的平衡条件,(在此较简单的情况下这一步可省

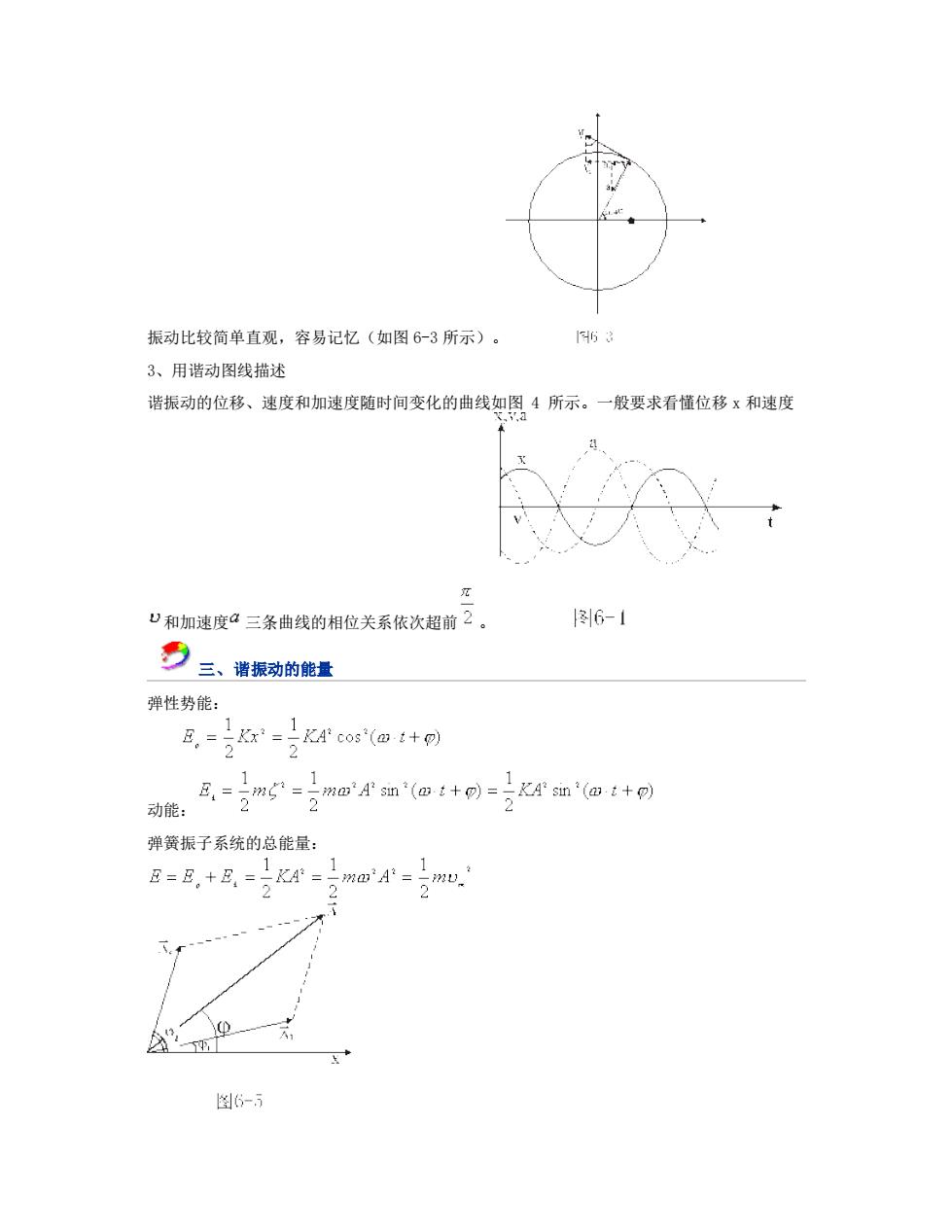
略)。 (3)给一微扰使物体偏离平衡位置,画出物体的受力图,找出回复力或回复力矩的表达 (4)列出动力学微分方程,与标准谐振动微分方程比较系数,可得谐振动的圆频率和周 期。 夕三、谐振动的运动学描述有三种形式: 1、解析式 谐振动的运动方程为X=Acos(@t+) 将此式分别对时间求一次,二次导数可相应得到振子的速度和加速度a随时间的函数表达 式: u=-四Asn(四t+) a=-a2Acos(@t+) 事实上速度”和加速度a还应是位移x的函数: U=±A-x a=-、x 在运动方程中圆频率四或周期T是由力学条件所确定的,而振幅A和初相位”是由初始条件 ∫x0=Aco89 所确定的。将=0代入位移x和速度"的表达式可得: g仰= 由此可解出: 四x。 2、用旋转矢量(即参考圆)描述 旋转矢量方=可,以匀角速西逆时针旋转,矢端M点在X轴上的投影P点的运动方程: 六,=Aos(@+)却好是谐振动方程,且M点匀速圆周运动的速度"和加速度2在X轴 上的投影”和2:也却好是P点在X轴上作谐振动的速度和加速度。所以用参考圆来描述谐
略)。 (3)给一微扰使物体偏离平衡位置,画出物体的受力图,找出回复力或回复力矩的表达 式。 (4)列出动力学微分方程,与标准谐振动微分方程比较系数,可得谐振动的圆频率和周 期。 二、谐振动的运动学描述有三种形式: 1、解析式 谐振动的运动方程为 将此式分别对时间求一次,二次导数可相应得到振子的速度 和加速度 a 随时间的函数表达 式: 事实上速度 和加速度 a 还应是位移 x 的函数: , 在运动方程中圆频率 或周期 T 是由力学条件所确定的,而振幅 A 和初相位 是由初始条件 所确定的。将 代入位移 和速度 的表达式可得: 由此可解出: , 2、用旋转矢量(即参考圆)描述 旋转矢量 ,以匀角速 逆时针旋转,矢端 M 点在 X 轴上的投影 P 点的运动方程: 却好是谐振动方程,且 M 点匀速圆周运动的速度 和加速度 在 X 轴 上的投影 和 也却好是 P 点在 X 轴上作谐振动的速度和加速度。所以用参考圆来描述谐
振动比较简单直观,容易记忆(如图6-3所示)。 3、用谐动图线描述 谐振动的位移、速度和加速度随时间变化的曲线如盟4所示。一般要求看懂位移x和速度 ”和加速度4三条曲线的相位关系依次超前2 6-1 号三、谱叛动的能量 弹性势能: =号=号o+ 动能: 8=img=2mA(@t+=写m@t+p) 2 弹簧振子系统的总能量 B=,+8=号=m=mu 图6-5
振动比较简单直观,容易记忆(如图 6-3 所示)。 3、用谐动图线描述 谐振动的位移、速度和加速度随时间变化的曲线如图 4 所示。一般要求看懂位移 x 和速度 和加速度 三条曲线的相位关系依次超前 。 三、谐振动的能量 弹性势能: 动能: 弹簧振子系统的总能量:

夕四、请装动的合成 1、同方向同频率两个谐振动的合成 设谐振动 x =A cos(a1+) x,=A cos(at+) 合成后的谐振动 x=X+x=Acos(@t+g》 A sin +A,sin, 式中:4=y4+4+244c08(0-月), gc+A,co 此关系式用旋转矢量图6-5则很容易理解和记忆。 当:%-%=2kπ 则 A=A+A 92-网=(2k+1)x 则 A=A-A 2、同方向频率相近的谐振动合成 =(@+m,) v= 合成后的圆频率为其平均圆频率 2 ,合成后产生的 拍频v=内-y, 3、互相垂直的谐振动合成 两个相互垂直的同频率谐振动合成的质点运动轨迹一般为椭圆,在一定条件下也可能为圆或 直线。轨迹的形状决定于两振动的相位差与振幅,当两个谐振动频率不相等,但有简单的整 数比时,质点的运动轨迹为李萨如图形。 夕五、阻尼报动 当弹簧振子在振动过程中受到的阻力与速度大小成正比与速度方向相反的阻力作用时,振子 d'x = 的动力学方程为: 式中严为阻尼系将共。。=物2月=户 则上式可改写为: +28+mx=0
四、谐振动的合成 1、同方向同频率两个谐振动的合成 设谐振动 合成后的谐振动 式中: ; 此关系式用旋转矢量图 6-5 则很容易理解和记忆。 当: 则 则 2、同方向频率相近的谐振动合成 合成后的圆频率为其平均圆频率 或其频率 ,合成后产生的 拍频 。 3、互相垂直的谐振动合成 两个相互垂直的同频率谐振动合成的质点运动轨迹一般为椭圆,在一定条件下也可能为圆或 直线。轨迹的形状决定于两振动的相位差与振幅,当两个谐振动频率不相等,但有简单的整 数比时,质点的运动轨迹为李萨如图形。 五、阻尼振动 当弹簧振子在振动过程中受到的阻力与速度大小成正比与速度方向相反的阻力作用时,振子 的动力学方程为: 式中 为阻尼系数。若令 , 则上式可改写为:
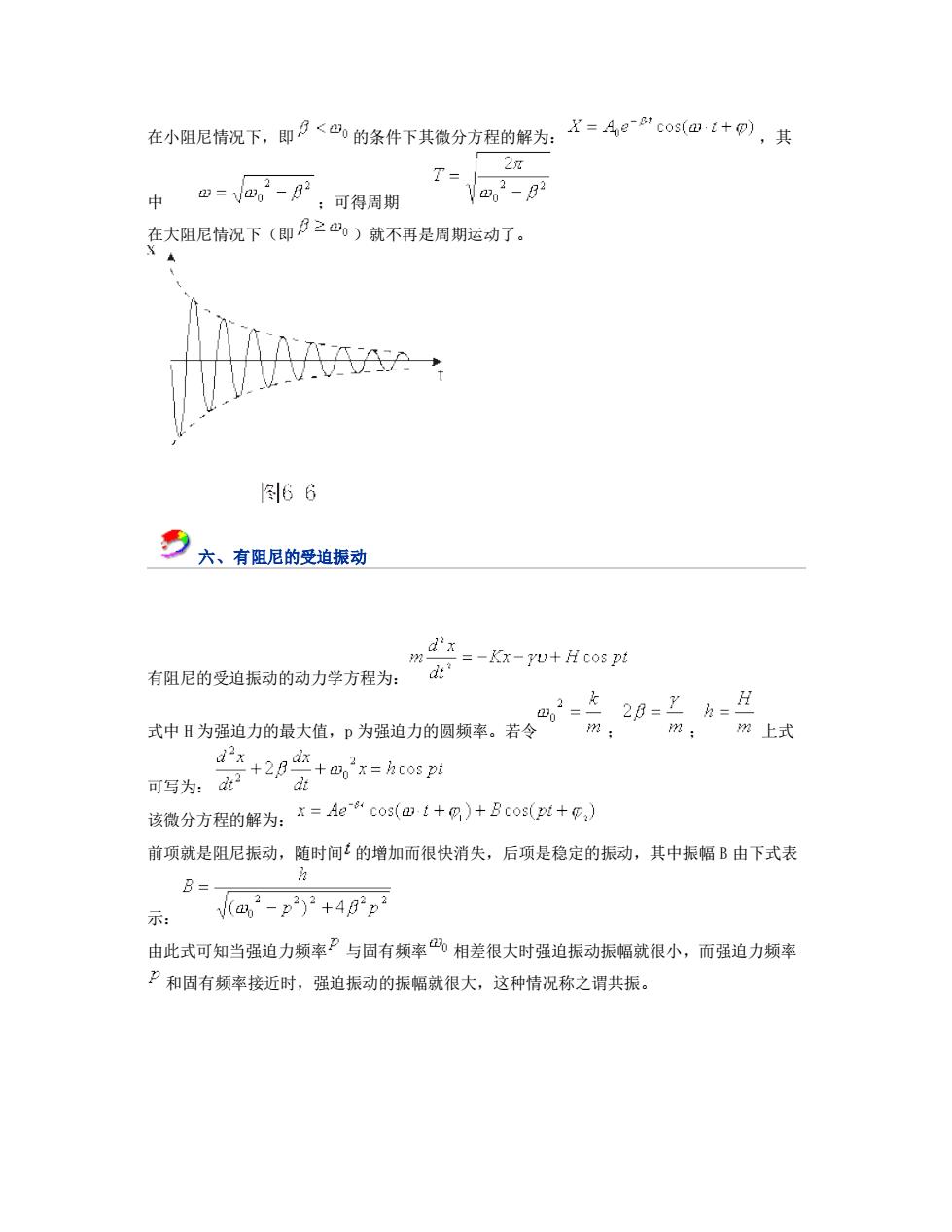
在小阻尼情况下,即月<的条件下其微分方程的解为: X=4ecos(四i+),其 T 中 西=V,2-B2 可得周期 Yao2-82 在大阻尼伤视下(御日2心)就不再是周期运动了。 7- 66 号六、有阻尼的受道银动 m=-Kx-u+Hcos p! 有阻尼的受迫振动的动力学方程为: 武中耳为强迫力的录大值,p为强地力的圆期半,古令心京,加二女二月 m: m上式 可写为:2+2月+2x=coe卫 at 该微分方程的解为:X=4e“co3(四1+g)+Bc0s(以+,) 前项就是阻尼振动,随时间的增加而很快消失,后项是稳定的振动,其中振幅B由下式表 B= 示 (2-p2)2+4B2p2 由此式可知当强迫力频率”与固有频率相差很大时强迫振动振幅就很小,而强迫力频率 P和固有频率接近时,强迫振动的振幅就很大,这种情况称之谓共振
在小阻尼情况下,即 的条件下其微分方程的解为: ,其 中 ;可得周期 在大阻尼情况下(即 )就不再是周期运动了。 六、有阻尼的受迫振动 有阻尼的受迫振动的动力学方程为: 式中 H 为强迫力的最大值,p 为强迫力的圆频率。若令 ; ; 上式 可写为: 该微分方程的解为: 前项就是阻尼振动,随时间 的增加而很快消失,后项是稳定的振动,其中振幅 B 由下式表 示: 由此式可知当强迫力频率 与固有频率 相差很大时强迫振动振幅就很小,而强迫力频率 和固有频率接近时,强迫振动的振幅就很大,这种情况称之谓共振

第6章振动力学基础 【例6-1】质量为血的木板,压在一轻弹簧上,弹簧的静压缩为0,木板静 止在平衡位置处:在木板上方高”=0处自由落下一与木板质量相同的泥块,它与木板作完 全非弹性碰撞, (1)写出碰撞后木板的运动方程。 (2)求从泥块与木板相碰到它们第一次回到相碰位置所用的时间。 (3)求任 位置处泥块与木块间的相互作用力。 图行-1a 短☒,-1h 【解】(1)题为竖直放置的弹簧振子,其解为: x=Acos(at+) 本题就是根据具体的条件确定谐振动方程中的,A和?。 22 再由初始条件确定A和。 碰撞后泥块与木板的平衡位置已不是原来木板的平衡位置了,而应满足: 2mg-k81=0 1=2mg-2g=2元 太洲g 得: 即在原来木板平衡位置下方位置处,我们如图b取坐标,新的平衡位置为坐标原点,x轴 向下,则泥块与木板碰撞瞬时的位置。=一。 泥块与木板碰撞瞬时满足动量守恒定律:州。=仰。十洲,)
第 6 章 振动力学基础 【例 6-1】质量为 m 的木板,压在一轻弹簧上,弹簧的静压缩为 ,木板静 止在平衡位置处;在木板上方高 处自由落下一与木板质量相同的泥块,它与木板作完 全非弹性碰撞, (1)写出碰撞后木板的运动方程。 (2)求从泥块与木板相碰到它们第一次回到相碰位置所用的时间。 (3)求任一位置处泥块与木块间的相互作用力。 【解】(1)题为竖直放置的弹簧振子,其解为: 本题就是根据具体的条件确定谐振动方程中的 和 。 再由初始条件确定 和 。 碰撞后泥块与木板的平衡位置已不是原来木板的平衡位置了,而应满足: 得: 即在原来木板平衡位置下方 位置处,我们如图 b 取坐标,新的平衡位置为坐标原点,x 轴 向下,则泥块与木板碰撞瞬时的位置 。 泥块与木板碰撞瞬时满足动量守恒定律:
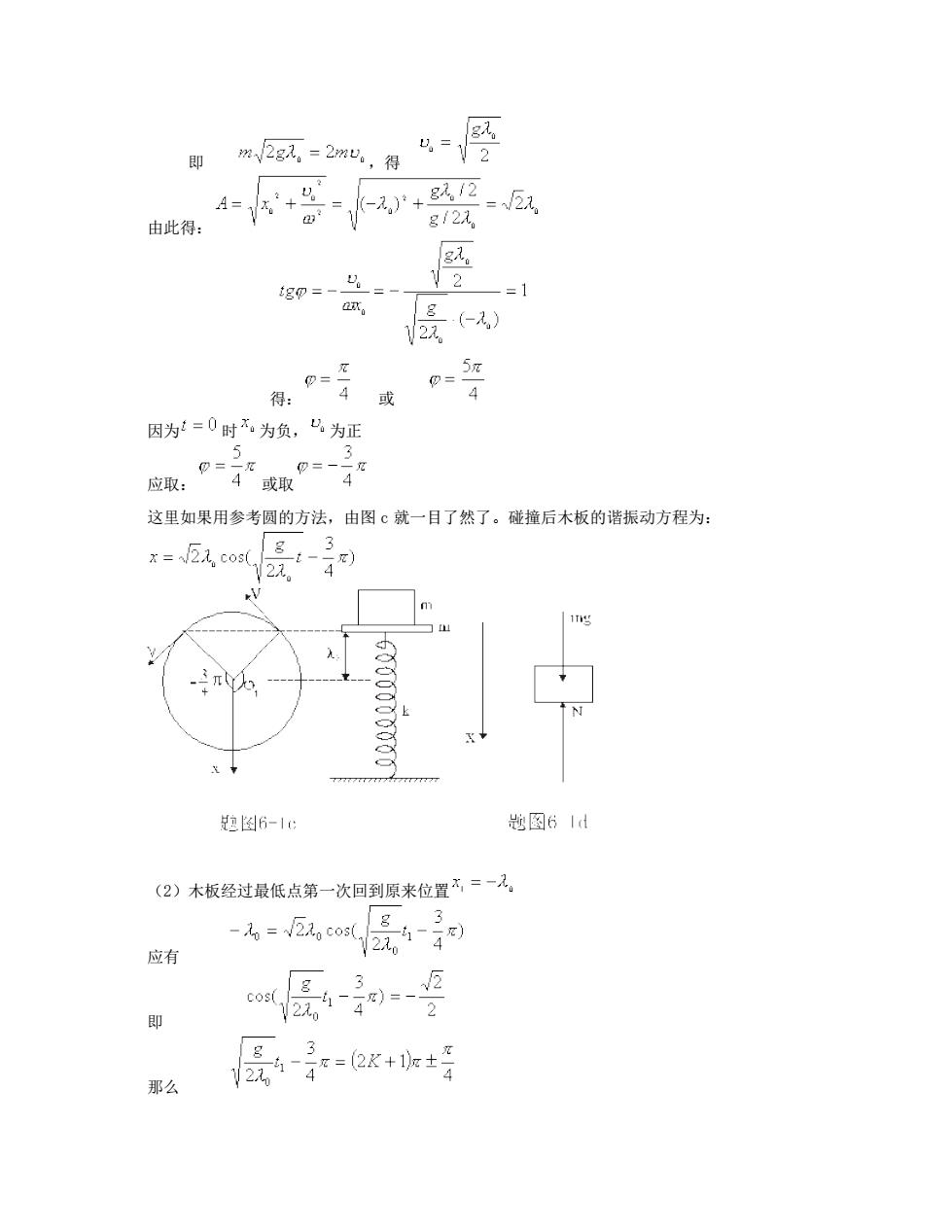
即m2g风=2mu,符 =2 4+ 由此得: -+ g121 g入 2=1 侵 得: 因为=0时不为负,8为正 这里如果用参考圆的方法,由图c就一目了然了。碰撞后木板的谐振动方程为: x-2,co2元 1吗 图6-1g 数图61d (2)木板经过最低点第一次回到原来位置不=一。 -6=风o侵4-刘 应有 即 2 「g 那么
即 ,得 由此得: 得: 或 因为 时 为负, 为正 应取: 或取 这里如果用参考圆的方法,由图 c 就一目了然了。碰撞后木板的谐振动方程为: (2)木板经过最低点第一次回到原来位置 应有 即 那么

2xx+e+号+2e=2K+次 2+- +=2+ 3 分析上式1为大于零的最小值应: 即: 用上解析分析是比较麻烦的,如采用参考圆就方便许多了,再参见图6-1℃,可见 名=人,"为负,为第二象限角,又参考圆半径为2孔,所以月子”。 参考圆旋转矢量以匀角速度四转动,可求得: 32 V812元2g 3 事实上从参考圆中可以看出旋转矢量矢端转过4个圆周,所以用时为: 图 (3)泥块的分离体受力图如图所示,列出相应的牛顿力学方程: g-2N=a=-w2x =mg+洲a2x=mg+四 相互作用力 g 可见x取正,即在平衡位置下方,相互作用力比泥块的重量大:而x取负,即在平衡位置上 方相互作用力比泥块小。 在最下方不=+23时 最大相互作用力: 火0,是 g =mg1+ 2 在最上方=-5入时 最小相互作用力 58050
分析上式 为大于零的最小值应: 即: 用上解析分析是比较麻烦的,如采用参考圆就方便许多了,再参见图 6-1c,可见 , 为负,为第二象限角,又参考圆半径为 ,所以 。 参考圆旋转矢量以匀角速度 转动,可求得: 事实上从参考圆中可以看出旋转矢量矢端转过 个圆周,所以用时为: (3)泥块的分离体受力图如图所示,列出相应的牛顿力学方程: 相互作用力 可见 x 取正,即在平衡位置下方,相互作用力比泥块的重量大;而 x 取负,即在平衡位置上 方相互作用力比泥块小。 在最下方 时 最大相互作用力: 在最上方 时 最小相互作用力

由此可知在整个谐振动过程中泥块不会跳离木板。 本题如坐标向上取,请读者考虑一下计算的结果有何不同? 号【例6-4】如果水平光清桌面上放着质量为”和%的二物块。它们之间被一根幅强 系数为的轻弹簧连接着,试求该系统的振动周期。 【解】方法一,取如图a所示的坐标,设弹簧原长为,系统在振动过程中某时刻物块州1和 心的能标分别为和,如国所示。分别对汽和%列出运动微分方程。 m y000000000 006000000 +上 题到6-4 图64h d'x =m di (1) (2) 日=-F=-K(x,-x-) (1)式(2)式分别改写成: (3) d (4) (4)式减(3)式: -(+,--=型 5=x。-x,-1 上式可改写为: ++=0 d2 812 1 7=2K2 VK(州+洲2】 由此得该系统的谐振动周期: 1%
由此可知在整个谐振动过程中泥块不会跳离木板。 本题如坐标向上取,请读者考虑一下计算的结果有何不同? 【例 6-4】如果水平光滑桌面上放着质量为 和 的二物块。它们之间被一根倔强 系数为 的轻弹簧连接着,试求该系统的振动周期。 【解】方法一,取如图 a 所示的坐标,设弹簧原长为 ,系统在振动过程中某时刻物块 和 的坐标分别为 和 ,如图所示,分别对 和 列出运动微分方程。 (1) (2) 又 (1)式(2)式分别改写成: (3) (4) (4)式减(3)式: 令 上式可改写为: 由此得该系统的谐振动周期:

方法二,在质心坐标系解:我们先讨论一下弹簧的长度与倔强系数的关系,设弹簧原长为 1,剪短以后的弹簧长为1,在相同力F作用下,剪短后的弹簧1的伸长量为△!,就要比 原弹簧来得小。由弹簧的倔强系数定义: 原来弹簧的倔强系数: 剪短后弹簧的倔强系数: 上二式相比余: KA-T 可知同一种弹簧它的倔强系数与它原长成反比。 由题意可知,弹簧对州和%的作用力是系统的内力,系统在谐振动过程中质心C的位置相 =1 当于被固定不动,作用于州的弹簧长度 所以作用于州物块的弹簧倔强系数 K3-K1=K- 》 =+%K 1 21十2 所以对于质量为州物块的弹簧振子的振动周期 -2-2 %+2 =2rx0+ 3=2 同理的弹簧振子周期 VX(31+m) 方法三,能量法解: 仍取如a图的坐标系,系统总机械能为: 上式对时间求导得: 即 d产+ +K-车-心-W=0 (5) 由于系统合外力等于零,系统动量守恒,因此
方法二,在质心坐标系解:我们先讨论一下弹簧的长度与倔强系数的关系,设弹簧原长为 ,剪短以后的弹簧长为 ,在相同力 作用下,剪短后的弹簧 的伸长量为 ,就要比 原弹簧来得小。由弹簧的倔强系数定义: 原来弹簧的倔强系数: 剪短后弹簧的倔强系数: 上二式相比余: 可知同一种弹簧它的倔强系数与它原长成反比。 由题意可知,弹簧对 和 的作用力是系统的内力,系统在谐振动过程中质心 的位置相 当于被固定不动,作用于 的弹簧长度 又根据上面讨论 所以作用于 物块的弹簧倔强系数 所以对于质量为 物块的弹簧振子的振动周期 同理 的弹簧振子周期 方法三,能量法解: 仍取如 a 图的坐标系,系统总机械能为: 上式对时间 求导得: 即 (5) 由于系统合外力等于零,系统动量守恒,因此