
第7章狭义相对论基础 夕一、狭义相对论基本假设 1、狭义相对性原理:物理定律对一切惯性系等价。 2、光速不变原理:真空中光速与光源或观察者的运动无关。 号二、时空相对性 = 1、动钟变慢效应: 1=1 2、动尺缩短效应: 号三、相对论运动产 1、洛仑兹坐标变换式: x' x-u y=y,z'=z.= v-u'le V1-u' xtut x=- t= v-u'fe y=y,2=z, -u'le 2、爱因斯坦速度变换式: 以=ue ,=-ue 1-总 y=心uE v-5.hwe 1+, 1+ 1+总 。 夕四、相对论动力学
第 7 章 狭义相对论基础 一、狭义相对论基本假设 1、狭义相对性原理:物理定律对一切惯性系等价。 2、光速不变原理:真空中光速 与光源或观察者的运动无关。 二、时空相对性 1、动钟变慢效应: 2、动尺缩短效应: 三、相对论运动学 1、洛仑兹坐标变换式: ; 。 2、爱因斯坦速度变换式: ; 。 四、相对论动力学

2。 1、相对论质量: = 龙话 方=成= 2、相对论动量: -ule 3、相对论动力学方程: dtdt -u'fe 夕五、相对论能量 1、相对论能量:E=州c 2、相对论动能:马。=州c-网,c 3、相对论静能:只=州,e 号大、相对论能基与动量关系 B=p'c'+mie
1、相对论质量: 2、相对论动量: 3、相对论动力学方程: 五、相对论能量 1、相对论能量: 2、相对论动能: 3、相对论静能: 六、相对论能量与动量关系

第7章狭义相对论基础 号【例T-】A钟静止在系的原皮P,B钟静止在”系的原点。现”系相对系以 恒定速度向右运动,当子点重合时,A、B两钟都调在零点上,在A钟读数为A时,从A 钟发出一个光信号,B钟接受到该信号时其读数为8,试问B钟相对A钟的速度为多大? 解:B钟接收到A钟光出的光信号时,B钟和A钟的距离和光讯号通过的距离相同,即: utB=C(a-Ta) (1) 这里B钟的读数为8,而上式中用的符号却是‘8,这是因为B钟再高速运动,是在”系钟的 读数,应是台=T。,当它反映到观测者的同一坐标了中,动钟变慢 = 。 T (2) 由(1)、(2)式解得B钟相对A钟运动的速度 S S +e C 姬图-1 号【例7-2】远方一里体以=08心相对地球运动,地球上接收到它辐射出的两次闪光之 间的时间间隔为5昼夜。试求下列两种情况下,在该星体上测得的闪光周期: (1)星体远离地球运动: (2)星体接近地球运动。 解:(1)设相对星体静止的闪光周期为△?”,相对地球的闪光周期为△T,则有 △T= △T 2 (1) 相对地球而言,设星体在A位置发出的第一闪光,经过△T时间后辐射第二闪光时,它已运动 到B位置,如图7-2所示。两闪光之间的距离为: B!=(c+)△T
第 7 章 狭义相对论基础 【例 7-1】A 钟静止在 系的原点 ,B 钟静止在 系的原点 。现 系相对 系以 恒定速度向右运动,当 与 点重合时,A、B 两钟都调在零点上,在 A 钟读数为 时,从 A 钟发出一个光信号,B 钟接受到该信号时其读数为 ,试问 B 钟相对 A 钟的速度 为多大? 解:B 钟接收到 A 钟光出的光信号时,B 钟和 A 钟的距离和光讯号通过的距离相同,即: (1) 这里 B 钟的读数为 ,而上式中用的符号却是 ,这是因为 B 钟再高速运动,是在 系钟的 读数,应是 ,当它反映到观测者的同一坐标 中,动钟变慢 (2) 由(1)、(2)式解得 B 钟相对 A 钟运动的速度 【例 7-2】远方一星体以 相对地球运动,地球上接收到它辐射出的两次闪光之 间的时间间隔为 5 昼夜。试求下列两种情况下,在该星体上测得的闪光周期: (1)星体远离地球运动; (2)星体接近地球运动。 解:(1)设相对星体静止的闪光周期为 ,相对地球的闪光周期为 ,则有 (1) 相对地球而言,设星体在 A 位置发出的第一闪光,经过 时间后辐射第二闪光时,它已运动 到 B 位置,如图 7-2 所示。两闪光之间的距离为:

建赵心一乃 拉网7心 (2)由于两闪光均以光速C传播,因此地球上接受到两闪光之间的时间间隔为 (3) 联立(1)(2)(3)式,并代入△:=5昼夜,解得固定在该星体上参考系测得的闪光周 c-v 5 期 事实上,这是光源以高速远离观察者运动时光的多普勒效应。观测到的周期变长,频率减少, 这是一种“红移”现象 (2)如果星体向着地球运动,应用相同的分析方法可得闪光的周期缩短,频率增加,引起 “紫移”现象。这是光源以高速向着观察者运动时光的多普勒效应。 s 【例7-3】试用质心运动定律求相对论质量。 【解】两个完全相同的小球A和B,在X'坐标系中,如题图7-3所示,分别以速度沿轴 的正方向和负方向运动。A和B的质心C相对于K坐标系静止。另取一K坐标系,为使B相对 于K系静止,使K系相对于K系以4沿正方向运动,(也就是让R系相对于K系以运 动)。根据相对论速度合成原理,A球相对于K系的速度: =1+e (1) 在K系中由上所述,B球的速度4=0,B球的质量为静止质量,=州,A球的质量为动质 量,二州,质心C相对于K系的速度为=:在K系中由质心运动定律 州心,+m,。=(m,+m:巴。 即: n)=H十2)·让 2 网u=m-)=州1+e- 、 得: c-u =c+ (e2+2-4c7月 =22 (c'+u') F73
(2) 由于两闪光均以光速 传播,因此地球上接受到两闪光之间的时间间隔为 (3) 联立(1)(2)(3)式,并代入 昼夜,解得固定在该星体上参考系测得的闪光周 期 昼夜。 事实上,这是光源以高速远离观察者运动时光的多普勒效应。观测到的周期变长,频率减少, 这是一种“红移”现象。 (2)如果星体向着地球运动,应用相同的分析方法可得闪光的周期缩短,频率增加,引起 “紫移”现象。这是光源以高速向着观察者运动时光的多普勒效应。 【例 7-3】试用质心运动定律求相对论质量。 【解】两个完全相同的小球 A 和 B,在 K'坐标系中,如题图 7-3 所示,分别以速度 沿 轴 的正方向和负方向运动。A 和 B 的质心 C 相对于 K'坐标系静止。另取一 K 坐标系,为使 B 相对 于 K 系静止,使 K'系相对于 K 系以 沿 正方向运动,(也就是让 K 系相对于 K'系以- 运 动)。根据相对论速度合成原理,A 球相对于 K 系的速度: (1) 在 K 系中由上所述,B 球的速度 ,B 球的质量为静止质量 ,A 球的质量为动质 量 ,质心 C 相对于 K 系的速度为 ;在 K 系中由质心运动定律: 即: 得:

Au'e %=1 (2) 由(1)式得 + 代入(2)式,得: 1 ,2 2。三 (c'+u' 。 证得: 夕【例7-4】试根据以下两例讨论光子的吸收和发射: (1)质量为”0的静止原子核(或原子),受到能量为的光子撞击,原子核(或原子)将 光子的能量全部吸收,则此合并系统的速度(反冲速度)以及静止质量各为多少? (2)静止质量为0的静止原子发出能量为的光子,则发射光子后原子的静止质量为多 大? 解:(1)设原子吸收光子后的静质量为以0,由能量守恒定律 moc2+8=Moc -2 (1) 由动量守恒定律 E Mo e (2) (0① m+_ u=- (2)可得 夜 c2+2 将“代入(1)式得 M=%c+E%,e+g 2 C
(2) 由(1)式得 代入(2)式,得: 证得: 【例 7-4】试根据以下两例讨论光子的吸收和发射: (1) 质量为 的静止原子核(或原子),受到能量为 的光子撞击,原子核(或原子)将 光子的能量全部吸收,则此合并系统的速度(反冲速度)以及静止质量各为多少? (2) 静止质量为 的静止原子发出能量为 的光子,则发射光子后原子的静止质量为多 大? 解:(1)设原子吸收光子后的静质量为 ,由能量守恒定律 (1) 由动量守恒定律: (2) 可得 得: 将 代入(1)式得

(3)同理,设发射光子后原子的静质量为6速度为“,由能量守恒定律 Mic Moe2-E= - 由动量守恒定律 28 联立 求得: M6=Moe
(3) 同理,设发射光子后原子的静质量为 速度为 ,由能量守恒定律 由动量守恒定律 联立 求得:

第7章狭义相对论基础 5 7.1两星之间的距离1.8×10“米,一飞船速度0.6c沿两星连线方向飞行。在星 体上的观测者测得飞船掠过这两星间距所用的时间为多少?飞船上的宇航员测得的时间为多 少?两星间的距离又为多少? 号7.2一观察者测得运动着的米尺长0,50,求此米尺以多大的速度相对观察者运 动? 号?.3一根直杆在5系中现察时,静止长度为,与不轴间的夹角为,若S系以建 度“相对于S系沿不轴正向运动,试求在S'系中观察,直杆的长度以及直杆与不轴间的夹 角。 9.4 ?介子是一不稳定粒子,在静止参考系中测得平均寿命为26×10*。若此 种粒子相对于实验室0.8c的速度运动。 (1)在实验室参考系中测量,?介子的寿命多长? (2)该?介子在衰变前运动了多长距离? 91.5 一惯性系中同一地点发生的两个事件,其先后时间间隔为0.2S:在另一惯性 系中测得此两事件的时间间隔为0,38,求这两个惯性系之间的相对运动速率。 夕?6原长即米的火前,垂直从地面起飞,到达某一高度后的速飞离地球。为定 此时火箭的速度,地面发射一光脉冲,并在火箭的尾部和头部的镜上反射,如地面收到尾部 反射光为200秒,收到头部反射光的脉冲比尾部光脉冲迟了17.4×10‘秒。计算: (1)火箭离地面的距离: (2)火箭相对地球的速度: (3)火箭上观测者测得头尾两反射镜收到光脉冲的时间差:
第 7 章 狭义相对论基础 7.1 两星之间的距离 米,一飞船速度 沿两星连线方向飞行。在星 体上的观测者测得飞船掠过这两星间距所用的时间为多少?飞船上的宇航员测得的时间为多 少?两星间的距离又为多少? 7.2 一观察者测得运动着的米尺长 0.5m,求此米尺以多大的速度相对观察者运 动? 7.3 一根直杆在 S 系中观察时,静止长度为 ,与 轴间的夹角为 ,若 S'系以速 度 相对于 S 系沿 轴正向运动,试求在 S'系中观察,直杆的长度以及直杆与 轴间的夹 角。 7.4 介子是一不稳定粒子,在静止参考系中测得平均寿命为 。若此 种粒子相对于实验室 的速度运动。 (1)在实验室参考系中测量, 介子的寿命多长? (2)该 介子在衰变前运动了多长距离? 7.5 一惯性系中同一地点发生的两个事件,其先后时间间隔为 ;在另一惯性 系中测得此两事件的时间间隔为 ,求这两个惯性系之间的相对运动速率。 7.6 原长 600 米的火箭,垂直从地面起飞,到达某一高度后匀速飞离地球。为测定 此时火箭的速度,地面发射一光脉冲,并在火箭的尾部和头部的镜上反射,如地面收到尾部 反射光为 200 秒,收到头部反射光的脉冲比尾部光脉冲迟了 秒。计算: (1)火箭离地面的距离; (2)火箭相对地球的速度; (3)火箭上观测者测得头尾两反射镜收到光脉冲的时间差;

号?字宙射线与大气相互作用能产生赛变。若在寿技高空产生爽变,放 出的严介子能在地面上观测到,已知静止的“介子平均考命”=2心,试在下列两个参考系 中计算放出的从介子的速度至少有多大? (1)以地面为参考系: (2)以“介子为参考系: 号8在惯性系了中观测,一粒子沿产轴正向运动,建度为如。若模性系了相对 S以0.9℃的速度沿x轴正向运动,试用下列两种变换式计算粒子相对S系的速度 (1)伽利略速度变换式: (2)狭义相对论速度变换式。 号79地球上一观察者看见一飞铅A以随度25x10四6从他身边飞达,另飞船B 以速度20×10物/s跟随A飞行。求: (1)A上的乘客看到B的相对速度: (2)B上的乘客看到A的相对速度。 立。人得佛止作长,顺为四,于是我得出专度为霜 此棒以速度”在棒长方向上运动,此人再测棒的线密度应为多少?若棒在垂直长度方向上运 动,它的线密度又为多少? 号1.1在太阳参考系S中观察,一束星光垂直地面向上,邀率灯,而地球以速率 。=3×10'洲8垂直于此光线运动。试求在地球参考系S中观察,此束星光的速率与方 号2由于太阳向调留空同辐射能量,每秒损夫的质量为10纪。求太闲的射 功率
7.7 宇宙射线与大气相互作用能产生 衰变。若在海拔 高空产生 衰变,放 出的 介子能在地面上观测到,已知静止的 介子平均寿命 ,试在下列两个参考系 中计算放出的 介子的速度至少有多大? (1)以地面为参考系; (2)以 介子为参考系; 7.8 在惯性系 S'中观测,一粒子沿 轴正向运动,速度为 。若惯性系 S'相对 S 以 的速度沿 轴正向运动,试用下列两种变换式计算粒子相对 S 系的速度: (1)伽利略速度变换式; (2)狭义相对论速度变换式。 7.9 地球上一观察者看见一飞船 A 以速度 从他身边飞过,另一飞船 B 以速度 跟随 A 飞行。求: (1)A 上的乘客看到 B 的相对速度; (2)B 上的乘客看到 A 的相对速度。 7.10 某人测得一静止棒长为 ,质量为 ,于是求得此棒线密度为 。假定 此棒以速度 在棒长方向上运动,此人再测棒的线密度应为多少?若棒在垂直长度方向上运 动,它的线密度又为多少? 7.11 在太阳参考系 S 中观察,一束星光垂直地面向上,速率为 ,而地球以速率 垂直于此光线运动。试求在地球参考系 S'中观察,此束星光的速率与方 向。 7.12 由于太阳向周围空间辐射能量,每秒损失的质量为 。求太阳的辐射 功率
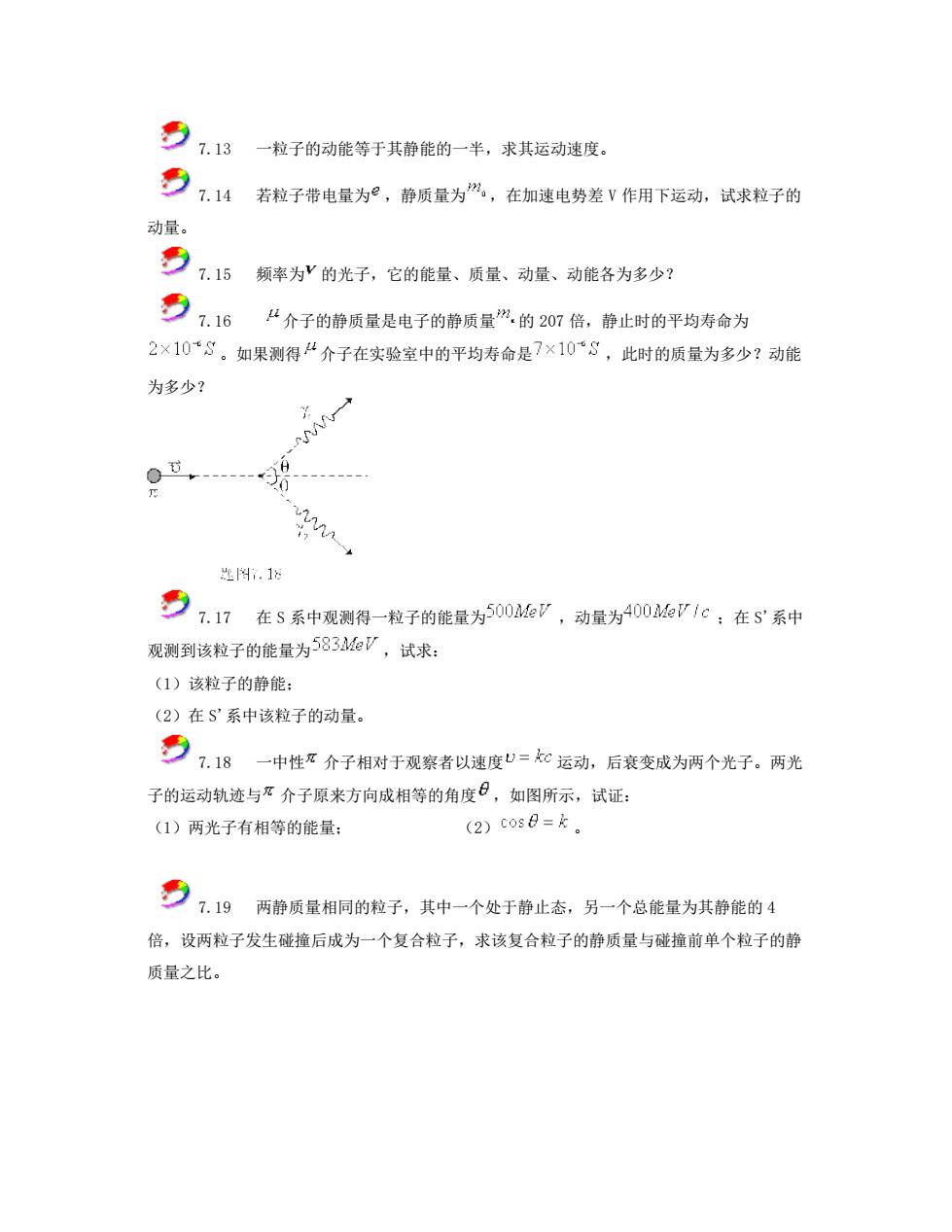
号7.13一粒子的动能等于其静能的一单,求其运动速度。 号.14若子带电量为,静质量为心,在加迷电势差v作用下运动。试求粒子的 动量。 2.15频事为的光子,它的能量、质量、动量、动能各为多少? 91.16 “介子的静质量是电子的静质量”,的207倍,静止时的平均寿命为 2×108。如果测得“介子在实验室中的平均寿命是7×10S,此时的质量为多少?动能 为多少? 匙.18 7.?在5系中观测得粒子的能量为0067,动量为0671C:在5系种 观测到该粒子的能量为583/,试求: (1)该粒子的静能: (2)在S'系中该粒子的动量。 号.18一中性:介子相对于观察者以速度心=如运动,后衰变成为两个光子。两光 子的运动轨迹与:介子原来方向成相等的角度日,如图所示,试证: (1)两光子有相等的能量: (2)cose=k 号?.19两静质最相同的粒子,灭中一个处于静止态,另一个总能量为其静能的1 倍,设两粒子发生碰撞后成为一个复合粒子,求该复合粒子的静质量与碰撞前单个粒子的静 质量之比
7.13 一粒子的动能等于其静能的一半,求其运动速度。 7.14 若粒子带电量为 ,静质量为 ,在加速电势差 V 作用下运动,试求粒子的 动量。 7.15 频率为 的光子,它的能量、质量、动量、动能各为多少? 7.16 介子的静质量是电子的静质量 的 207 倍,静止时的平均寿命为 。如果测得 介子在实验室中的平均寿命是 ,此时的质量为多少?动能 为多少? 7.17 在 S 系中观测得一粒子的能量为 ,动量为 ;在 S'系中 观测到该粒子的能量为 ,试求: (1)该粒子的静能; (2)在 S'系中该粒子的动量。 7.18 一中性 介子相对于观察者以速度 运动,后衰变成为两个光子。两光 子的运动轨迹与 介子原来方向成相等的角度 ,如图所示,试证: (1)两光子有相等的能量; (2) 。 7.19 两静质量相同的粒子,其中一个处于静止态,另一个总能量为其静能的 4 倍,设两粒子发生碰撞后成为一个复合粒子,求该复合粒子的静质量与碰撞前单个粒子的静 质量之比

第7章狭义相对论基础 少容案 7.1 100s 80s 1.44×1010m 7.2 26×108翔1图 7.3 c3c0s2) weets 7.4(1)433×10s:(2) 104m 7.5 22×103m18 7.6 3×1010m 09c, 2×10-5s 7.71)0998c: (2)0988c 7.8(1) 18c (2)0994c 7.9 (1)-1125×10m1:(2)1125×103m1s 0 i-hu 0 7.10 7.11c, 20.6 7.1236×1026 7.1322×10m1s 7.14 hvme 7.15,c2,c, 7.167245m. 517.5mc3 .17(1)300e7,(2)500始r1c7.19316 少振示 7.6(2)见图 2 1=1 2b2-46c=09 解得 U=c2aE2+45
第 7 章 狭义相对论基础 答案 7.1 , , 7.2 7.3 , 7.4 (1) ; (2) 7.5 7.6 , , 7.7 (1) ; (2) 7.8 (1) ; (2) 7.9 (1) ;(2) 7.10 ; 7.11 , 7.12 7.13 7.14 7.15 , , , 7.16 ; 7.17 (1) ;(2) 7.19 提示 (2)见图 , 解得