
第11章静电场 夕一、库仑定律 真空中1和92两个点电荷之间相互作用力的规律 瓦=-克=49 1g4 1=9×102 式中比例常数 牛顿·米2/库仑3 真空中的介电常数气=885×10“库仑2/牛额·米3 夕二、电场强度 1、定义:电场中某点的电场强度的量值等于单位正电荷所受的力,电场强度的方向就是正 8、 电荷受力的方向,定义式为: 90 式中90为试验电荷,电场强度是空间坐标的单值函数。 2、场强迭加原理,电场中任一点的总场强等于各带电体在该点产生场强的矢量和: 点电荷系: -2成-2月 =小8=∫西产 连续带电体: 对于线电荷分布 d相应 dq =oris dg 体电荷分布 相脸出= 号三、真空中的高斯定强 在真空中的任何静电场中,通过任何闭合曲面的电通量等于这闭合曲面所包围的电荷数和的 0分之一 。 应用高斯定理时必须注意:
第 11 章 静电场 一、库仑定律 真空中 和 两个点电荷之间相互作用力的规律 式中比例常数 牛顿·米 / 库仑 真空中的介电常数 库仑 / 牛顿·米 二、电场强度 1、定义:电场中某点的电场强度的量值等于单位正电荷所受的力,电场强度的方向就是正 电荷受力的方向,定义式为: 式中 为试验电荷,电场强度是空间坐标的单值函数。 2、场强迭加原理,电场中任一点的总场强等于各带电体在该点产生场强的矢量和: 点电荷系: 连续带电体: 对于线电荷分布 相应 ; 面电荷分布 相应 体电荷分布 相应 三、真空中的高斯定理: 在真空中的任何静电场中,通过任何闭合曲面的电通量等于这闭合曲面所包围的电荷数和的 分之一。 。 应用高斯定理时必须注意:

1、式中的:是闭合曲面内的电荷,而计算电通量中的场强豆是闭合曲面内和外的电荷所产 生的合场强。 2、高斯定理是一个普遍规律,适用于真空中任何静电场,但要用高斯定理来计算场强,那 么电荷分布必须要具有特定的对称性。 高斯定理说明了电力线起始于正电荷,终止于负电荷,即静电场是有源场, 号四、电势与电劳差 1、静电场环流定律 f克d=0 这说明静电场是保守场,试验电荷在任何静电场中移动时,电场力所作的功只与试验电荷的 大小以及路径的起点和终点位置有关,而与路径无关。 2、电势能 电场力所作的功等于电势能的减少 形-两=w=g∫豆成 定义在无限远处的电势能用,=形为零时,真空中某点口的电势能 w。=g「豆 3、电势 电场中某点的电势等于单位正电荷放在该点处时的电势能,也就等于单位正电荷任 意路径移到无限远处电场力所作的功,即 4、电势差 0.-0,=-形=jE g 5、电势迭加原理 点电荷系电场中某点的电势等于每个点电荷单独在该点产生电势的代数和 0=0+0++.=2 连续分布电荷系的电场中某点的电势
1、式中的 是闭合曲面内的电荷,而计算电通量中的场强 是闭合曲面内和外的电荷所产 生的合场强。 2、高斯定理是一个普遍规律,适用于真空中任何静电场,但要用高斯定理来计算场强,那 么电荷分布必须要具有特定的对称性。 高斯定理说明了电力线起始于正电荷,终止于负电荷,即静电场是有源场。 四、电势与电势差 1、静电场环流定律 这说明静电场是保守场,试验电荷在任何静电场中移动时,电场力所作的功只与试验电荷的 大小以及路径的起点和终点位置有关,而与路径无关。 2、电势能 电场力所作的功等于电势能的减少 定义在无限远处的电势能 为零时,真空中某点 的电势能 3、电势 电场中某点的电势等于单位正电荷放在该点处时的电势能,也就等于单位正电荷任 意路径移到无限远处电场力所作的功,即 4、电势差 5、电势迭加原理 点电荷系电场中某点的电势等于每个点电荷单独在该点产生电势的代数和 连续分布电荷系的电场中某点的电势

v= 6、场强与电势的梯度关系 某方向上的场强 如在直角坐标系中,在x、)、2三个方向上的分量为 a aU B,= 原则上讲来,电势是标量,场强是矢量,一般先计算电势再利用求偏导数的方法来求场强各 个方向的分量,比直接矢量计算场强来得简便,但应注意到计算的电势必须是电势随空间坐 标的函数关系,而不是特定点的电势,对特定点(如:球心、圆心等)的场强,用场强与电 势的梯度关系来计算并不方便。 号五、几#带电系统的场层与电州 1、点电荷9 = U= 4π8r1 4π6r 2、电偶极子市=g (r> 2 2= 1 轴线的延长线上: 中垂线上: 4π8 U= 任意点处 Ansr 3、均匀带电1的直线电荷 E 元(6m8-m8) B,= ()
6、场强与电势的梯度关系 某 方向上的场强 如在直角坐标系中,在 、 、 三个方向上的分量为 , , 原则上讲来,电势是标量,场强是矢量,一般先计算电势再利用求偏导数的方法来求场强各 个方向的分量,比直接矢量计算场强来得简便,但应注意到计算的电势必须是电势随空间坐 标的函数关系,而不是特定点的电势,对特定点(如:球心、圆心等)的场强,用场强与电 势的梯度关系来计算并不方便。 五、几种带电系统的场强 与电势 1、点电荷 2、电偶极子 轴线的延长线上: 中垂线上: 任意点处 3、均匀带电 的直线电荷

特例:无限长直线电荷 ,26 E=0 4、均匀带电9的细圆环轴线上 B= 5、面电荷密度均匀为圆盘轴线上(圆盘半径为R) -(1-cos0 2 U=+R-对 2% 6、均匀带电·无限大平面 U。-U。=E(x2-x) 8=G 7、平行板电容器内 0 U。-U。=E(x-) 平行板电容器外 8=0 8、均匀带电为已的半径为R的球面 球面内E=0 UAR 球面外 8= 9、均匀带电为的半径为R的球体(体电荷分布)
特例:无限长直线电荷 4、均匀带电 的细圆环轴线上 5、面电荷密度均匀为 圆盘轴线上(圆盘半径为 ) 6、均匀带电 无限大平面 7、平行板电容器内 平行板电容器外 8、均匀带电为 的半径为 的球面 球面内 球面外 9、均匀带电为 的半径为 的球体(体电荷分布)

0=23R2-3 球体内 46R 8x6R3 球体外 10、单位长度均匀带电无无限长圆柱面 柱面内E=0 柱面外
球体内 球体外 10、单位长度均匀带电 无限长圆柱面 柱面内 柱面外
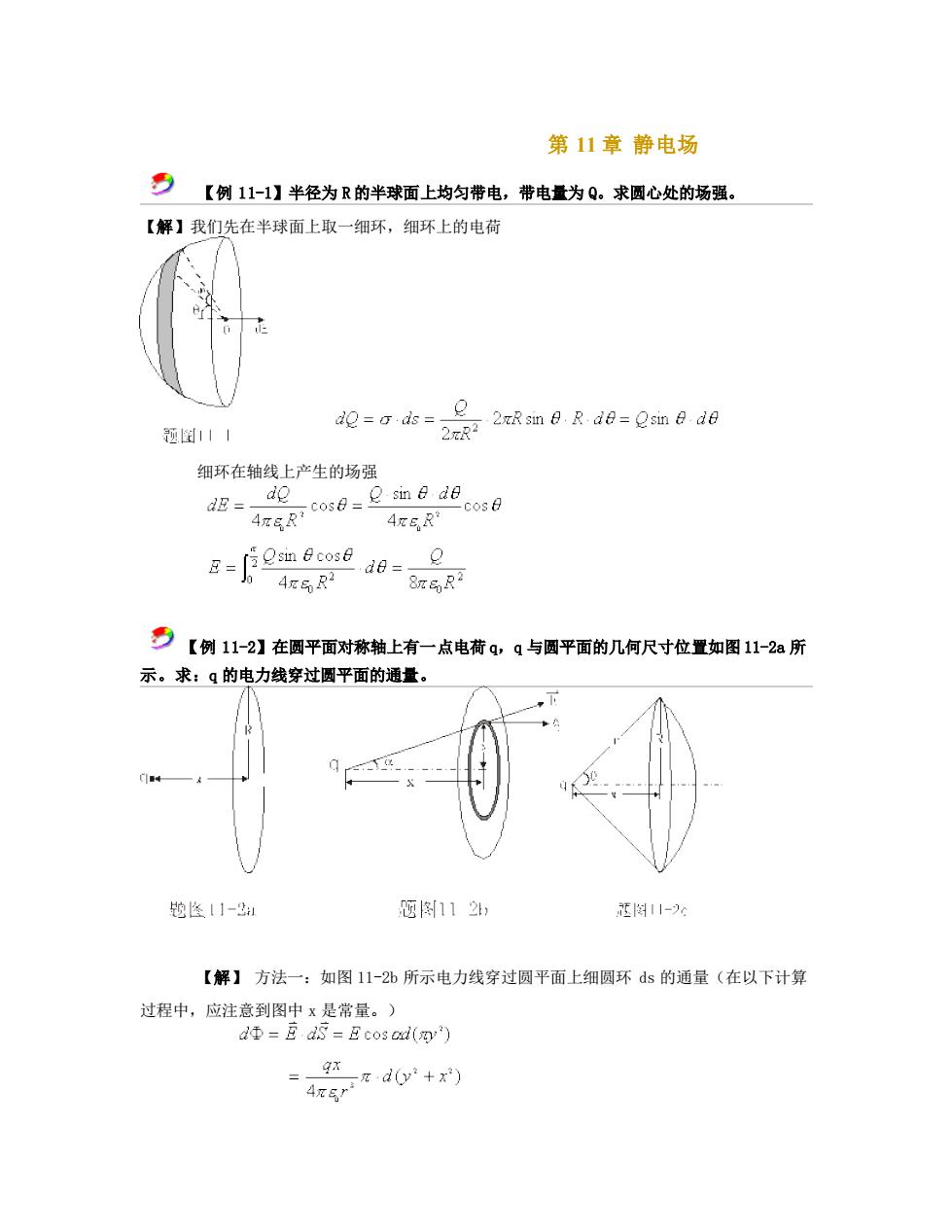
第11章静电场 夕【例11=1】半径为R的半球面上均匀带电,带电量为Q。求圆心处的场强。 【解】我们先在半球面上取一细环,细环上的电荷 题图111 dR de-m d0 细环在轴线上产生的场强 6ow0-ee0eos6 dE=- 4E5R g-9me0=a 4x气R2 号【例1-2】在圆平面对称轴上有一点电荷0,9与圆平面的几何尺寸位置如图1-2a所 示。求:q的电力线穿过圆平面的通量。 毯性11-2利 您112, 阁11-c 【解】方法一:如图11-2b所示电力线穿过圆平面上细圆环ds的通量(在以下计算 过程中,应注意到图中x是常量。) dΦ=E5=cosod() ed0+ =
第 11 章 静电场 【例 11-1】半径为 R 的半球面上均匀带电,带电量为 Q。求圆心处的场强。 【解】我们先在半球面上取一细环,细环上的电荷 细环在轴线上产生的场强 【例 11-2】在圆平面对称轴上有一点电荷 q,q 与圆平面的几何尺寸位置如图 11-2a 所 示。求:q 的电力线穿过圆平面的通量。 【解】 方法一:如图 11-2b 所示电力线穿过圆平面上细圆环 ds 的通量(在以下计算 过程中,应注意到图中 x 是常量。)

=9x动 。T毁影 1 26 式中8如图c中所示。 方法二:如图c所示,穿过圆平面的电通量与穿过图示球冠的电通量相等。穿过包围点电荷q 闭合球面的总电量为8。,再由球冠面积S=2(一)占总球面面积4g中的比率,就可求 出球冠的电通量。由此求得圆平面的电通量: 枣s4×20y-=g1-5=号0-cos0 4 28。 ⊙【例11-3】一半径为的无限长带电圆柱体,其体电荷密度三%( P0为常数,”为离圆柱体轴线的距离。试求: (1)圆柱体内外各处的电场强度。 (2)求出场强最大值的位置在何处,场强多大? (3)求轴线处的电势。 【解】(1)如题图11-3所示,作高斯面5,由高斯定理 手g6=旦 (1) 高斯面内的9可通过体电荷积分求得: g-jp2or-jn吃点)2wt 2 代入(1)式: 题图11-8
式中 如图 c 中所示。 方法二:如图 c 所示,穿过圆平面的电通量与穿过图示球冠的电通量相等。穿过包围点电荷 q 闭合球面的总电量为 ,再由球冠面积 S=2 占总球面面积 中的比率,就可求 出球冠的电通量。由此求得圆平面的电通量: 【例 11-3】一半径为 的无限长带电圆柱体,其体电荷密度 ,其中 为常数, 为离圆柱体轴线的距离。试求: (1)圆柱体内外各处的电场强度。 (2)求出场强最大值的位置在何处,场强多大? (3)求轴线处的电势。 【解】(1)如题图 11-3 所示,作高斯面 S,由高斯定理 (1) 高斯面内的 可通过体电荷积分求得: 代入(1)式:

(2) 可见,当”<时,E为正,即沿半径方向向外 当’之@时,即圆柱体外场强为0 d祖=0 (2)场强最大的位置满足: dr 0--0 r= 得 3”处场强最大,代入(2)式得场强的最大值 18g (3)轴线处的电势 号【例1-4】一厚度水的无限大平板型区域中均匀分布着电荷,电荷体密度为。 (1)求板内外场强的分布,并画出场强分布曲线(), (2)若取中心面的电势为零,试求在意位置处的电势,并画出相应的电势分布曲线闭
(2) 可见,当 时, 为正,即沿半径方向向外 当 时,即圆柱体外场强为 0 (2)场强最大的位置满足: 即 得 处场强最大,代入(2)式得场强的最大值 (3)轴线处的电势 【例 11-4】一厚度为 的无限大平板型区域中均匀分布着电荷,电荷体密度为 。 (1)求板内外场强的分布,并画出场强分布曲线 ; (2)若取中心面的电势为零,试求任意位置处的电势,并画出相应的电势分布曲线

【解】在均匀带电平板内如题图11-4妇所示,对称地作一高斯面 B.8+8.S=p 2xs 由高斯定理 当 得 3s=p如 + 对闭合柱面心,由高斯定理 得 2 得 十+ 由此可画出场强8()曲线图1-4h。 在板内三<x<2任意点的电势,由电势的 式:0-0w=8a 得: 因=-欧=0-紧本=号 .-w=8x+8, -管+袋 题国11 = 得 8284586250 同样
【解】在均匀带电平板内如题图 11-4a 所示,对称地作一高斯面 S 由高斯定理 当 得: 对闭合柱面 ,由高斯定理 当 , 得 当 , 得 由此可画出场强 曲线图 11-4b。 在板内 任意点的电势,由电势的定义 式: 得: 板外 任意点的电势 得 同样:

由此可画出(W曲线分布图1-4c 下面再看一看这场强曲线和电势曲线间的相互关系。 在x>0的区域场强豆沿不正方向:在x<0的区域场强豆是沿着不的负方向。场强的方向应 是电势降落的方向,在X=0处。=0,因此整个区域内的电势都为负值。还应注意到电势曲 线上的斜率的负值应等于场强的大小,也就是场强大的位置电势曲线的斜率大,即电势的变化 率大,场强小的地方电势的变化率小。场强为零的位置为电势的极值位置。 号【例1-5】电荷密度均匀为P的球体内,有一球形空腔,如题图1山-5©所示,我们将坐 标原点建立在球心上,空腔球心的位置矢量为。 (1)试求空腔内任意点的场强。 (2)若球体半径为!,空腔半径为,试求空腔球心处的电势 01 题图11 粒图11-5利 【解】(1)我们采用补偿方法来求解,设想原球体没有空腔,为正体电荷十P充满,而再设 想在空腔位置放体电荷P的球体,正、负体电荷相消,相当于一空腔。 利用高斯定理可求均匀带电(没有空腔的)球体内的任意点的场强。 豆=
由此可画出 曲线分布图 11-4c 下面再看一看这场强曲线和电势曲线间的相互关系。 在 的区域场强 沿 正方向;在 的区域场强 是沿着 的负方向。场强的方向应 是电势降落的方向,在 处 ,因此整个区域内的电势都为负值。还应注意到电势曲 线上的斜率的负值应等于场强的大小,也就是场强大的位置电势曲线的斜率大,即电势的变化 率大,场强小的地方电势的变化率小。场强为零的位置为电势的极值位置。 【例 11-5】电荷密度均匀为 的球体内,有一球形空腔,如题图 11-5a 所示,我们将坐 标原点建立在球心上,空腔球心的位置矢量为 。 (1)试求空腔内任意点的场强。 (2)若球体半径为 ,空腔半径为 ,试求空腔球心处的电势 【解】(1) 我们采用补偿方法来求解,设想原球体没有空腔,为正体电荷 充满,而再设 想在空腔位置放体电荷 的 球体,正、负体电荷相消,相当于一空腔。 利用高斯定理可求均匀带电(没有空腔的)球体内的任意点的场强