
第1章质点运动学 夕直线运动 质点沿者直线轨道运动,称为直线运动。 1、运动方程:就是质点运动时,其所在的位置的坐标x随 时间变化的函数关系。 x=x) 2、速度: dt 3、加速度: 4、运动方程曲线,速度图线,加速度图线及相互关系: 图11为匀变速运动图线间的相互关系,在图中可以看到: 瞬时速度日在量值上等于x~(图线上相应各点 的切线斜率,瞬时加速度a在量值等于U~:图 线上相应各点切曲斜率。~图线 中t→(+6:时间内所包围的面积等于该时间内速 度0)的增量。8~t图线中t→+△:时间 内所包围的面积等于该时间的位移。 夕曲线运动 1、运动方程 (1)位置矢量户:在参照系上选定的坐标原点0到运动质点p的有向线段啦=广。 在直角坐标系中: 产=++z ((2)运动方程:运动质点的位置矢量随时间变化的函数关系·
第 1 章 质点运动学 直线运动 质点沿着直线轨道运动,称为直线运动。 1、运动方程:就是质点运动时,其所在的位置的坐标 x 随 时间变化的函数关系。 2、速度: 3、加速度: 4、运动方程曲线,速度图线,加速度图线及相互关系: 图 1-1 为匀变速运动图线间的相互关系,在图中可以看到: 瞬时速度 在量值上等于 图线上相应各点 的切线斜率,瞬时加速度 在量值等于 图 线上相应各点切曲斜率。 图线 中 时间内所包围的面积等于该时间内速 度 的增量。 图线中 时间 内所包围的面积等于该时间的位移。 曲线运动 1、运动方程 (1)位置矢量 :在参照系上选定的坐标原点 o 到运动质点 p 的有向线段 。 在直角坐标系中: (2)运动方程:运动质点的位置矢量随时间变化的函数关系

(3)轨道方程:运动质点在空间运动轨迹的空间坐标的函数表达式。 要正确区分运动方程和轨道方程。 2、位移、速度和加速度 (1)位移:位置矢量的增量。 △F=+△)-F 要正确区分位移和路程。位移△广表示质点位置改 变是一个矢量,路程g是△:时间内质点所走 轨迹的长度,是个标量(参阅图1-2)。在一般情况 下,路程与位移矢量的模是不等的。即: △s≠ 、吹 (2)速度:位置矢量随时间的变化率: dt 在直角坐标系 中: 图12 速率: u=同=西++u 要正确区分速度与速率。速度是矢量,其方向永远沿着 轨道的切线方向:速率是标量,表示速度的大小。瞬时 速率与瞬时速度的大小相等,但一般情况下,平均速率 与平均速度的大小并不相等。 (3)加速度:速度矢量随时间的变化率: a=d'r 或位置矢量对时间的二阶微商: 在直角坐标系中: =aitaj+ak
(3)轨道方程:运动质点在空间运动轨迹的空间坐标的函数表达式。 要正确区分运动方程和轨道方程。 2、位移、速度和加速度 (1)位移:位置矢量的增量。 要正确区分位移和路程。位移 表示质点位置改 变是一个矢量,路程 是 时间内质点所走 轨迹的长度,是个标量(参阅图 1-2)。在一般情况 下,路程与位移矢量的模是不等的。即: (2)速度:位置矢量随时间的变化率: 在直角坐标系 中: 速率: 要正确区分速度与速率。速度是矢量,其方向永远沿着 轨道的切线方向;速率是标量,表示速度的大小。瞬时 速率与瞬时速度的大小相等,但一般情况下,平均速率 与平均速度的大小并不相等。 (3)加速度:速度矢量随时间的变化率: 或位置矢量对时间的二阶微商: 在直角坐标系中:

(4)切向加速度和法向加速度 把质点运动的轨道的切线方向和法线方向作为坐标系来看 我们称它为自然坐标系。在自然坐标系中: a=a,tta=f+心分 p 豆:切向加速度,反映速率的变化。4>0,质点 作速率增加运动。在圆周运动特例 中,a=a(a为角速度) 云。:法向加速度,反映速度方向的变化,永远指向轨迹 曲线的凹向,P为曲率半径,并非质点到坐标原点的 距离。在圆周运动特例中, a.=Ro *平面极坐标系中的速度与加速度: 位置矢量: 产= Γata ☒13 速度: 式中,”为径速度,r为横向速度。 a=西=ar+a,0 加速度: 为径向加速度 +24d8 正为横向加 速度。 号运动的志如性和相对性 1、运动的迭加原理要明确运动迭加原理是从实验事实总结出来的客观规律。根据迭加原理 可把质点的运动看为不同的分运动的迭加。通常选用的是正交合成和分解
(4)切向加速度和法向加速度 把质点运动的轨道的切线方向和法线方向作为坐标系来看 我们称它为自然坐标系。在自然坐标系中: :切向加速度,反映速率的变化。 ,质点 作速率增加运动。在圆周运动特例 中, ( 为角速度) :法向加速度,反映速度方向的变化,永远指向轨迹 曲线的凹向, 为曲率半径,并非质点到坐标原点的 距离。在圆周运动特例中, 。 * 平面极坐标系中的速度与加速度: 位置矢量: 速度: 式中, 为径速度, 为横向速度。 加速度: 式中, 为径向加速度 为横向加 速度。 运动的迭加性和相对性 1、运动的迭加原理 要明确运动迭加原理是从实验事实总结出来的客观规律。根据迭加原理 可把质点的运动看为不同的分运动的迭加。通常选用的是正交合成和分解

2、相对运动 (1)位置矢量关系 从图中我们可直接得到:产=无+户 (2)速度关系(在平动参照系中) 因为: y't 式中:0一绝对速度,质点相对于参照系K的速度: 可一一牵连速度,参照系K相对于参照系K的速度。 一相对速度,质点相对于参照系K的速度。 (3)加速度关系: a= do 因为 正,我们可得:i=d,+d 式中:云一一绝对加速度,质点相对于参照系K的速加 图11 度: 。一一牵连加速度,参照系K相对于参照系K的加速 度: 在,一一相对加速度,质点相对于参照系K的加速度
2、相对运动 (1)位置矢量关系 从图中我们可直接得到: (2)速度关系(在平动参照系中) 因为: ,我们可得: 式中: ——绝对速度,质点相对于参照系 K 的速度; ——牵连速度,参照系 K'相对于参照系 K 的速度; '——相对速度,质点相对于参照系 K'的速度。 (3)加速度关系: 因为 ,我们可得: 式中: ——绝对加速度,质点相对于参照系 K 的速加 度; ——牵连加速度,参照系 K'相对于参照系 K 的加速 度; '——相对加速度,质点相对于参照系 K'的加速度

第1章质点运动学 乡【例1-1山质点在一平面内运动,其位置矢量为广,速度为可,试说 d d同 出:正、、 的物理意义。并指出它们分别为零时,除了 表示静止外,还可表示质点作何种运动? d 【解】正中月为位置矢量的模(一般可用”表示),它表示质点离原点的距 d 止表示质点到原点距离的变化率,即径向速度八,。当它为零时,表明质点与原点的 距离”不变,表示质点的运动轨迹为圆。即当”≠0时,质点作圆周运动。 表示质点的速率大小”。当它为零时,即产为恒量,所以只能表示质点静止。 d 表示质点的速率”的变化率,即切向加速度“,。当它为零时,表示质点作匀 速率运动。 由表示加速度的大小。当它为零时,表示速度立为恒量,除了表示质点静止外,还 可表示质点作匀速直线运动。 号【创1-2】以初速可=平抛一物体,求抛出后t秒钟时,物体的切向加速皮和法 向加速度。 【解】任意时刻1物体的速度:4=内; U,=gt 它的速率: u=+出=2+g2甲 g2 切向加速度: a,=g2-a= g", 法向加速度: u,2+g22 阁1- 事实上,抛体运动任意时刻的加速度始终为8。重力加速度g沿着切线方向的分
第 1 章 质点运动学 【例 1-1】质点在一平面内运动,其位置矢量为 ,速度为 ,试说 出: 、 ; 、 的物理意义。并指出它们分别为零时,除了 表示静止外,还可表示质点作何种运动? 【解】 中 为位置矢量的模(一般可用 表示),它表示质点离原点的距 离。 表示质点到原点距离的变化率,即径向速度 。当它为零时,表明质点与原点的 距离 不变,表示质点的运动轨迹为圆。即当 时,质点作圆周运动。 表示质点的速率大小 。当它为零时,即 为恒量,所以只能表示质点静止。 表示质点的速率 的变化率,即切向加速度 。当它为零时,表示质点作匀 速率运动。 表示加速度的大小。当它为零时,表示速度 为恒量,除了表示质点静止外,还 可表示质点作匀速直线运动。 【例 1-2】以初速 平抛一物体,求抛出后 t 秒钟时,物体的切向加速度和法 向加速度。 【解】任意时刻 t 物体的速度: ; 它的速率: 切向加速度: 法向加速度: 事实上,抛体运动任意时刻的加速度始终为 。重力加速度 g 沿着切线方向的分

量为切向加速度,g在法线方向上的分量即为法向加速度。 由题图1-2几何关系直接可得: 切向加速度: 法向加速度: u2+g2 【例1-3】长为?的梯子上端A贴在垂直的墙上,梯上有一点站离梯子下端B增 的距离为b,如题图(1-38)。当B点沿水平地面离开墙脚向外滑动过程中: 求:(1)M点的运动轨迹。 (2)当B点以速度”滑离墙脚x处,则A点和M点的速度和加速度多 大?(设1=5米,b2米,x3米, U =2米/秒) 【解】(1)取如题图1-3(a)的坐标系。A、B坐标分别为:A (0,y),B(x,0)。 可得M点的位置坐标为: 不M=月丽cosp=0-)osg (1) B yM MBsmn o=bsm (2) 从()、(2)式中消去”,可得: XM 代入已知条件,得: 。所以,M点的运动轨迹 为椭圆。 则图1-3 (2)因为A、B两点的约束关系为: x4+12=}“ (3) 把(3)式两边对时间t求一次导数,得:
量为切向加速度,g 在法线方向上的分量即为法向加速度。 由题图 1-2 几何关系直接可得: 切向加速度: 法向加速度: 【例 1-3】长为 的梯子上端 A 贴靠在垂直的墙上,梯上有一点 M,离梯子下端 B 端 的距离为 b,如题图(1-3a)。当 B 点沿水平地面离开墙脚向外滑动过程中: 求:(1)M 点的运动轨迹。 (2)当 B 点以速度 滑离墙脚 x 处,则 A 点和 M 点的速度和加速度多 大?(设 =5 米,b=2 米,x=3 米, =2 米/秒 ) 【解】(1)取如题图 1-3(a)的坐标系。A、B 坐标分别为:A (0,y),B(x,0)。 可得 M 点的位置坐标为: (1) (2) 从(1)、(2)式中消去 ,可得: 代入已知条件,得: 。所以,M 点的运动轨迹 为椭圆。 (2)因为 A、B 两点的约束关系为: (3) 把(3)式两边对时间 t 求一次导数,得:

2xU+2yU,=0 代入已知条件,得: =2=-1/秒 y 把(3)式两边对时间t求二次导数,得: u+心+a,=0 代入已知条件,得: a,=-+-2+1 -=-1.56米/秒 y 4 对于M点,因为: 分别代入(1)、(2)式得: 00-0昏, yu=2y (4) 分别把(4)式对时间t求一阶、二阶导数,可得: 0 ; 0-Ev. 代入已知条件,得: 6-亏2=12米/秒 au=0 w号1)。06冰/秒 0w=号-150 =-0.62米/秒2 在题图()中可以看到,梯子上各点速度和加速度的分布情况。少分布与日 的分布类似在题图(6)中省略未表示出来。 号【例1-】汽车静止时看到雨下落的方向与垂直方向偏东8,当汽车以速 度么,向东行驶时,测得雨下落方向与垂直方向偏西离8,求雨速。 【解】方法一:选取如题图1-4(a)坐标系,则雨速: D=usin 0i +ucosej (1) 车 速 元。=y (
代入已知条件,得: 把(3)式两边对时间 t 求二次导数,得: 代入已知条件,得: 对于 M 点,因为: 分别代入(1)、(2)式得: ; (4) 分别把(4)式对时间 t 求一阶、二阶导数,可得: ; ; 代入已知条件,得: ; ; 在题图(b)中可以看到,梯子上各点速度和加速度的分布情况。 分布与 a 的分布类似在题图(b)中省略未表示出来。 【例 1-4】汽车静止时看到雨下落的方向与垂直方向偏东 ,当汽车以速 度 向东行驶时,测得雨下落方向与垂直方向偏西离 ,求雨速。 【解】方法一:选取如题图 1-4(a)坐标系,则雨速: (1) 车 速 (
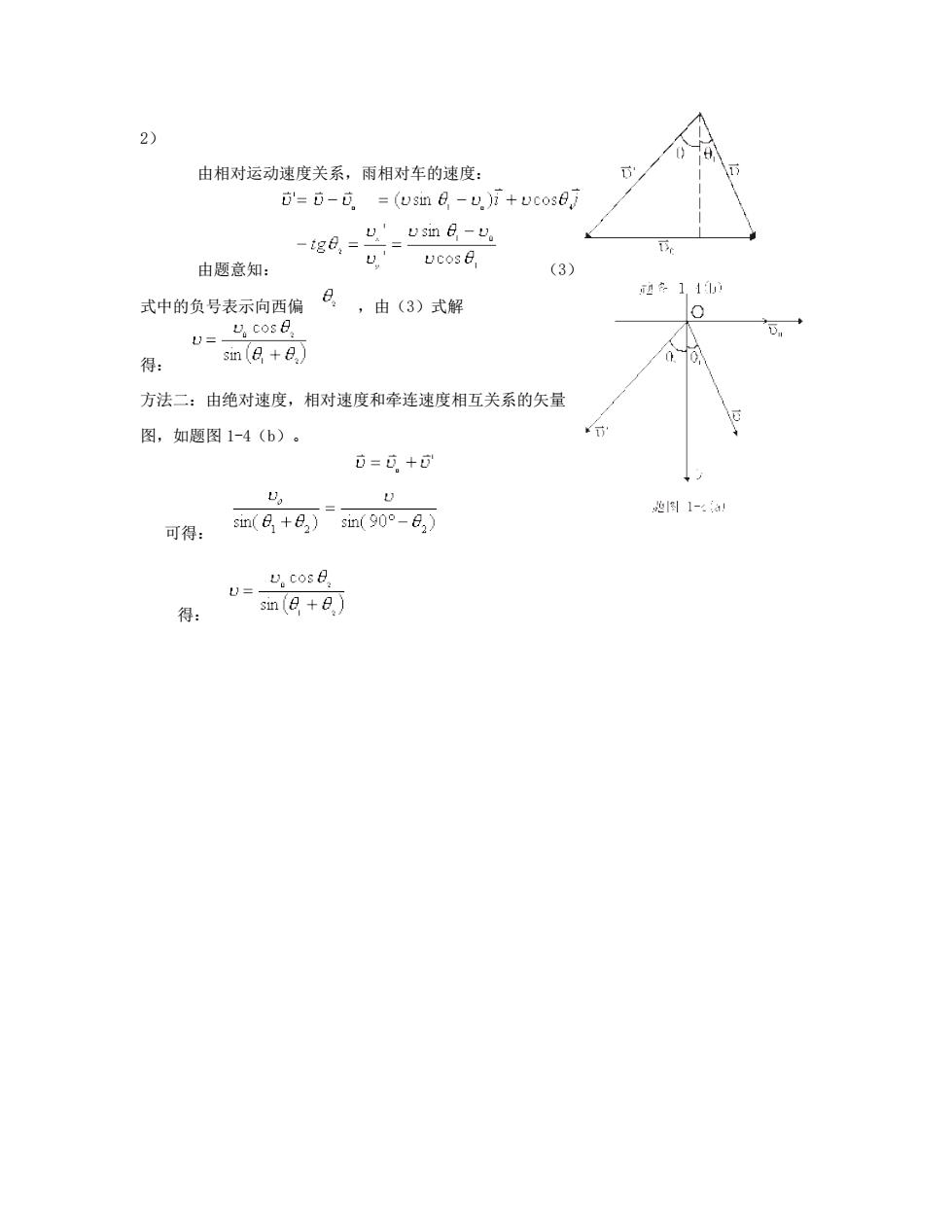
由相对运动速度关系,雨相对车的速度: B'=0-0.=(vsin e -v)+Dcose] -g8=g-vm8-8 由题意知: ,' Ucos (3) 式中的负号表示向西偏8,由(3)式解 得: u=ma+8】 B.cos e 方法二:由绝对速度,相对速度和牵连速度相互关系的矢量 图,如题图1-4(b)。 0=0+ 可得:m(8+8)m(90°-8 1-:a 得:
2) 由相对运动速度关系,雨相对车的速度: 由题意知: (3) 式中的负号表示向西偏 ,由(3)式解 得: 方法二:由绝对速度,相对速度和牵连速度相互关系的矢量 图,如题图 1-4(b)。 可得: 得:

第1章质点运动学 1,2某质点的运动方程曲线如图a所示,B为抛物线的一部分。试在图b、Q中画 出与该运动曲线相应的速度图线和加速度图线的大致情况,并扼要地说明该质点的运动情 况。 题1.2图 一辆汽车沿着笔直的公路行驶,速度与时间的关系如图中折线OABCDEF所示 (1)试画出加速度-时间变化曲线: (2)根据速度-时间曲线计算汽车在整个行驶过程中走过的路程和位移。 1. 题1.8图 一重物起吊装置如图所示,C为动滑轮,B为定滑轮。现以速率抽拉绳 子,试求滑轮C在x位置时重物的速度和加速度
第 1 章 质点运动学 1.2 某质点的运动方程曲线如图 a 所示,AB 为抛物线的一部分。试在图 b、c 中画 出与该运动曲线相应的速度图线和加速度图线的大致情况,并扼要地说明该质点的运动情 况。 l.3 一辆汽车沿着笔直的公路行驶,速度与时间的关系如图中折线 OABCDEF 所示。 (1)试画出加速度-时间变化曲线; (2)根据速度-时间曲线计算汽车在整个行驶过程中走过的路程和位移。 1.8 一重物起吊装置如图所示,C 为动滑轮,B 为定滑轮。现以速率 抽拉绳 子,试求滑轮 C 在 x 位置时重物的速度和加速度

9 1.9一质点在XY平面上运动,运动方程为: x=2, y=19 (1)计算并图示质点运动的轨迹: (2)写出t=28时,质点的位置矢量式: (3)写出2s末的瞬时速度和瞬时加速度矢量式。 (4)什么时候位置矢量与速度矢量垂直,这时它们的x,y分量各为多少? (5)质点何时离原点最近,求出相应的距离r。 9 1.14 一质点在高度处以初速度水平抛出,计算质点轨迹在抛出点和落地 点处的曲率半径。 题1.14图 题1.17图 号1.1?质点P向若x正方向的A点运动:已知0A=/。设1=0时质点位于 坐标原点,质点在其间任意时刻的速率正比于它所在位置至A点的距离,比例常数为k。试求 质点位置x,速率”和加速度4随时间变化的规律。 号1.18一升降机以加速度122州。2上升,当上升速率为244m。时,有- 螺帽自升降机的天花板上松落,天花板与升降机的底面相距2.74如,分别取下列两种坐标系计 算,螺帽从天花板落到底面所需的时间:螺帽相对于升降机外固定柱子的下降距离。 (1)坐标固定在地面上: (2)坐标固定在升降机上 号119如图所示,在水平面上有一直角三枝柱,它高为=0切, 宽1=03州。在A的项点有一质点B。A和B从静止开始同时加速运动,A的水平加速
1.9 一质点在 XY 平面上运动,运动方程为: , (1)计算并图示质点运动的轨迹; (2)写出 时,质点的位置矢量式; (3)写出 2s 末的瞬时速度和瞬时加速度矢量式。 (4)什么时候位置矢量与速度矢量垂直,这时它们的 x,y 分量各为多少? (5)质点何时离原点最近,求出相应的距离 r。 1.14 一质点在高度 h 处以初速度 水平抛出,计算质点轨迹在抛出点和落地 点处的曲率半径。 1.17 质点 P 向着 x 正方向的 A 点运动,已知 。设 时质点位于 坐标原点,质点在其间任意时刻的速率正比于它所在位置至 A 点的距离,比例常数为 k。试求 质点位置 x,速率 和加速度 随时间变化的规律。 1.18 一升降机以加速度 上升,当上升速率为 时,有一 螺帽自升降机的天花板上松落,天花板与升降机的底面相距 2.74m,分别取下列两种坐标系计 算,螺帽从天花板落到底面所需的时间;螺帽相对于升降机外固定柱子的下降距离。 (1)坐标固定在地面上; (2)坐标固定在升降机上。 1.19 如图所示,在水平面上有一直角三棱柱 A,它高 , 宽 。在 A 的顶点有一质点 B。A 和 B 从静止开始同时加速运动,A 的水平加速