
第15章磁介质 夕一、物质的磁化 1、磁介质中的磁场 设真空中的慰感应强度为的磁场中,放进了某种磁介质,在磁场和磁介质的相互作用 下,磁介质产生了附加磁场,这时磁场中任意一点处的磁感应强度 B=。+ 2、磁导率 由于磁介质产生了附加磁场户磁介质中的酷场5不再等于原米真空中的磁场瓦,定义8和 B0的比值为相对磁导率: 420 介质中的磁导率:4=从,内 式中4为真空中的磁导率 3、三种磁介质 (1)顺磁质:顺磁质产生的与0方向相同,且8八B,。 B=Bo+B' 4远大于1 夕二、藏化强度证 = 1、磁化强度定义为单位体积中分子磁矩的矢量和即: 2、磁化强度M与分子面电流密度」的关系: 式中产为磁介质外法线方向上的单位矢量。 }证i= 3、磁化强度班的环流 即磁化强度对闭合回路的线积分等于通过回路所包围面积内的总分子电流 三、磁介质中的安培环路定律
第 15 章 磁介质 一、物质的磁化 1、磁介质中的磁场 设真空中的磁感应强度为 的磁场中,放进了某种磁介质,在磁场和磁介质的相互作用 下,磁介质产生了附加磁场 ,这时磁场中任意一点处的磁感应强度 2、磁导率 由于磁介质产生了附加磁场 磁介质中的磁场 不再等于原来真空中的磁场 ,定义 和 的比值为相对磁导率: 介质中的磁导率: 式中 为真空中的磁导率 3、三种磁介质 (1)顺磁质:顺磁质产生的 与 方向相同,且 。 略大于 1 (2)抗磁质:抗磁质产生的 与 方向相反,且 。 略小于 1 (3)铁磁质:铁磁质产生的 与 方向相同,且 。 远大于 1 二、磁化强度 1、磁化强度 定义为单位体积中分子磁矩的矢量和即: 2、磁化强度 与分子面电流密度 的关系: 式中 为磁介质外法线方向上的单位矢量。 3、磁化强度 的环流 即 磁化强度对闭合回路的线积分等于通过回路所包围面积内的总分子电流 三、磁介质中的安培环路定律

1、安培环流定律在有磁介质条件下的应用 B-h(∑4+')=∑4+4'-∑+a fE-0i=21 即: 月=且-应 2、磁场强度定义为: ∫炉i-工1 3、磁介质中的安培环路定律: 4、应用磁介质中的安培环路定律的注意点: (1)庄的环流只与传导电流有关,与介质(或分子电流)无关。 (2)庄的本身( )既有传导电流也与分子电流有关。及既描写了传导电流 磁场的性质也描写了介质对磁场的影响。 (3)要应用磁介质中的安培环路定律来计算磁场强度H时,传导电流和磁介质的分布都必 须具有特殊的对称性。 5、磁介质中的几个参量间的关系: (1)磁化率老州 (2)B与H的关系 B=i+4M=42+飞4月=(1+x*)4月 B=4 (3)“与老"等之间的关系 4=4,=(1+老)4 4,=1+x0 乡国、藏场的边界条件(界面上无传导电流)
1、安培环流定律在有磁介质条件下的应用 即: 2、磁场强度定义为: 3、磁介质中的安培环路定律: 4、应用磁介质中的安培环路定律的注意点: (1) 的环流只与传导电流有关,与介质(或分子电流)无关。 (2) 的本身( )既有传导电流也与分子电流有关。 既描写了传导电流 磁场的性质也描写了介质对磁场的影响。 (3)要应用磁介质中的安培环路定律来计算磁场强度 时,传导电流和磁介质的分布都必 须具有特殊的对称性。 5、磁介质中的几个参量间的关系: (1)磁化率 (2) 与 的关系 (3) 与 等之间的关系 四、磁场的边界条件(界面上无传导电流)

u. 图15-1 1、磁介质分界面两边磁感应强度的法向分量连续,即: 2、磁介质分界面两边的磁场强度的切向分量连续,即: 3、磁感应线的折射定律 g月=丛 g84 (8意义如图15-1所示) 夕五、肤赋物质 1、磁畴:电子自旋磁矩取向相同的小区域。 2、磁化曲线(图15-2中B曲线) 3、磁导率曲线(图15-2中“曲线) 4、磁滞回线(图15-3) 图中三:为饱和磁感应强度 B,为剩磁,:为矫顽力。 图152 5、铁磁质与非铁磁质的主要区别: 铁磁物质产生的附加场的比原来真空中的磁场大得多。由于磁畴的存在,引起磁沛 现象:因此严格的说亚=疗,百=炉及相联系的公式不再成立,而且百与户的方向 也是不一定相同。如要上式成立则式中的:或“是一个变量,是一个多值函数和点函数, 如果作为常量的话,只是某种特定条件下(如静态时)的近似处理。 在铁磁质中,以下公式仍然是正确的,如: = △:
1、磁介质分界面两边磁感应强度的法向分量连续,即: 2、磁介质分界面两边的磁场强度的切向分量连续,即: 3、磁感应线的折射定律 ( 意义如图 15-1 所示) 五、铁磁物质 1、磁畴:电子自旋磁矩取向相同的小区域。 2、磁化曲线(图 15-2 中 曲线) 3、磁导率曲线(图 15-2 中 曲线) 4、磁滞回线(图 15-3) 图中 为饱和磁感应强度 为剩磁, 为矫顽力。 5、铁磁质与非铁磁质的主要区别: 铁磁物质产生的附加磁场 的比原来真空中的磁场 大得多。由于磁畴的存在,引起磁滞 现象;因此严格的说 , 及相联系的公式不再成立,而且 与 的方向 也是不一定相同。如要上式成立则式中的 或 是一个变量,是一个多值函数和点函数, 如果作为常量的话,只是某种特定条件下(如静态时)的近似处理。 在铁磁质中,以下公式仍然是正确的,如: ; ;

5店5=0ai=∑ 等 B+ -He 15-3 号大、电介质与磁介质的比较表 电介质 磁介质(非铁介质) 极化现象:电介质中的有极分子和无极磁化现象:在外磁场作用下,磁介质中 分子在外电场作用下发生转向极化和位的分子电流的磁矩在一定程度上沿着磁 移极化,在介质表面出现极化电荷。 场方向排列或和分子附加磁矩与外磁场 反向排列,在介质表面出现束缚电流 微观模型 分子电矩 产。=g 分子磁矩 描述状态 电极化强度 磁极化强度 的物理量 M= Av A形 界面上出现极化电荷面密度 界面上出现磁化表面电流 (束缚电荷) (束缚电流)密度 效 o=Pn '=证×府 p ds=-g M di=1' 价质对场 极化电荷的场强为卫 磁化分子面电流产生的磁场为 的影响 合场强 合磁感强度 应=。+ B=B。+
; ;等 六、电介质与磁介质的比较表 电 介 质 磁介质(非铁介质) 现 象 极化现象:电介质中的有极分子和无极 分子在外电场作用下发生转向极化和位 移极化,在介质表面出现极化电荷。 磁化现象:在外磁场作用下,磁介质中 的分子电流的磁矩在一定程度上沿着磁 场方向排列或和分子附加磁矩与外磁场 反向排列,在介质表面出现束缚电流。 微观模型 分子电矩 分子磁矩 描述状态 的物理量 电极化强度 磁极化强度 宏 观 效 果 界面上出现极化电荷面密度 (束缚电荷) 界面上出现磁化表面电流 (束缚电流)密度 介质对场 的影响 极化电荷的场强为 合场强 磁化分子面电流产生的磁场为 合磁感强度

辅助 电位移矢量 方 磁场强度 物理量 =2+2 基本场 fDd拔=∑go f8 ds=0 方程 啦i=0 ai-, 极化和 M=飞月 磁化规律 参 D=豆+P=nE+x,园 B=4豆+班=4应+4Xn月 量 =(1+x,)马E=8,, 上1+x)日=4,4月 间 下9 基 武中: 武中: 6,=1+x 4=1+x 6,6=8 4= 系 边值 耳:=E2: Bix=Bi Hy=Ha 关系 g月_西 g8242
辅助 物理量 电位移矢量 磁场强度 基本场 方程 极化和 磁化规律 参 量 间 基 本 关 系 式中: 式中: 边 值 关 系

第15章磁介质 号【例15-1】一根无限长直圆柱形铜导线,外包一层相对藏导率为的因筒形磁介 质,导线半轻为,磁介质的外半轻为,导线内均匀流过电流1。如图15-1a所示。 求 1)磁介质内、外的磁场强度、藏感应强度的分布,并面出()和)曲线(红为磁场 中某点离开圆柱轴线的距离)。 (2)磁介质内、外表面的磁化电流
第 15 章 磁介质 【例 15-1】一根无限长直圆柱形铜导线,外包一层相对磁导率为 的圆筒形磁介 质,导线半径为 ,磁介质的外半径为 ,导线内均匀流过电流 I。如图 15-1a 所示。 求: (1)磁介质内、外的磁场强度、磁感应强度的分布,并画出 和 曲线(r 为磁场 中某点离开圆柱轴线的距离)。 (2)磁介质内、外表面的磁化电流
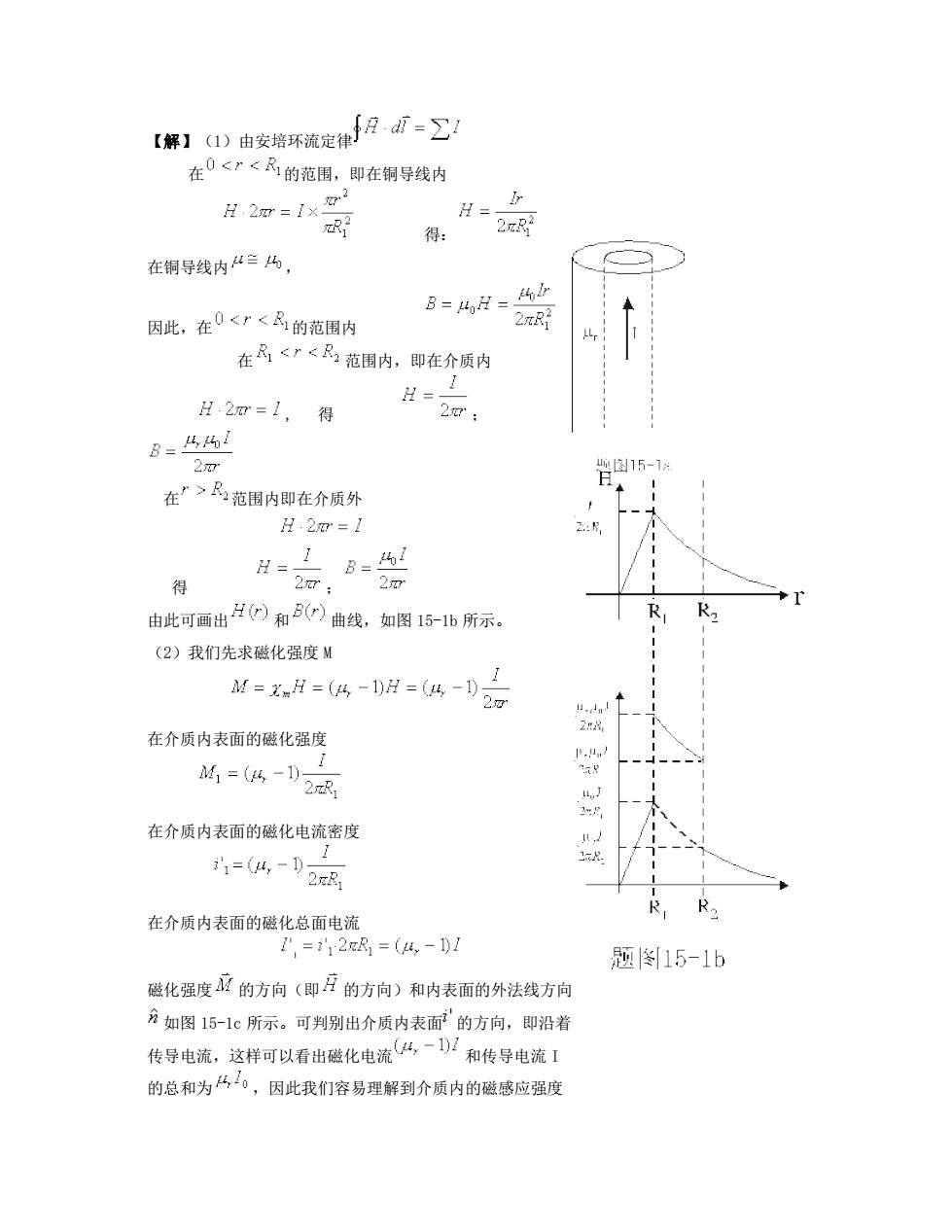
【解】1)由安培环流定律J月d=∑ 在0品范围内即在介质外 H.2m=1 H: 20 由此可画出H0和5曲线,如图15-1b所示。 (2)我们先求磁化强度M 在介质内表面的磁化强度 4=%-D2城 在介质内表面的磁化电流密度 =(4,-02R 在介质内表面的磁化总面电流 1,=128=(4,-1Dl 题15-1b 磁化强度的方向(即庄的方向)和内表面的外法线方向 方如图15-1c所示。可判别出介质内表面的方向,即沿着 传导电流,这样可以看出磁化电流4,一)/和传导电流1 的总和为4。,因此我们容易理解到介质内的磁感应强度
【解】(1)由安培环流定律 在 的范围,即在铜导线内 得: 在铜导线内 , 因此,在 的范围内 在 范围内,即在介质内 , 得 ; 在 范围内即在介质外 得 ; 由此可画出 和 曲线,如图 15-1b 所示。 (2)我们先求磁化强度 M 在介质内表面的磁化强度 在介质内表面的磁化电流密度 在介质内表面的磁化总面电流 磁化强度 的方向(即 的方向)和内表面的外法线方向 如图 15-1c 所示。可判别出介质内表面 的方向,即沿着 传导电流,这样可以看出磁化电流 和传导电流 I 的总和为 ,因此我们容易理解到介质内的磁感应强度

比真空情况下增大了倍的道理了。 以同样的方法可以计算出介界外表面的磁化电流密度 ,=亚×元,它的大小,=(4,-1,它的方向与传导 n+ *6 电流方向相反(如图15-1c所示)。这样我们容易理解在 ?>凡即真空部分,由于介界内、外两表面磁化电流大小 相同,方向相反,因此它们在对介质外的磁场就没有影响句 满足2m。 题图15Ic 号【创15-2】一无限长细导线,通有电流1,在左、右两侧充满相对磁导率分别为“ 和“2的均匀磁介质,如图15-2所示。试求两种磁介质中B、H和以。 【解】由磁场边界条件,两介质界面处法向连续,在离导线电流距离相同的界面处的圆周 上,两介质内的磁感应强度 Bi =B2s =B 根据介质中的安培环流定理,在离电流1的圆周上有 Hdl =1 即:月对+名g=1 风= B 在均匀介质内有 42 8+B -)m=1 代入上式得 41马 品12I B= 解出 4,+42a H1= B 41 4,12 相应得磁场强度 磁化强度 是物调
比真空情况下增大了 倍的道理了。 以同样的方法可以计算出介界外表面的磁化电流密度 ,它的大小 ,它的方向与传导 电流方向相反(如图 15-1c 所示)。这样我们容易理解在 即真空部分,由于介界内、外两表面磁化电流大小 相同,方向相反,因此它们在对介质外的磁场就没有影响仍 满足 。 【例 15-2】一无限长细导线,通有电流 I,在左、右两侧充满相对磁导率分别为 和 的均匀磁介质,如图 15-2 所示。试求两种磁介质中 、 和 。 【解】由磁场边界条件,两介质界面处法向连续,在离导线电流距离相同的界面处的圆周 上,两介质内的磁感应强度 根据介质中的安培环流定理,在离电流 I 的圆周上有 即: 在均匀介质内有 , 代入上式得 解出 相应得磁场强度 ; 磁化强度

41(42-101 M2(41+32河 图152 号【例15-3】一根沿轴向均匀磁化的细长永磁棒,磁化强度为,求图中各点的 和H。 45 。1 ·3 阁153 【解】由=疗×分可知M表示磁棒单位长度上的磁化电流,长直水磁棒相当于一个长直螺 线管。可以直接写出图示各点的磁感应强度: 51=4MB2=五=0 瓦=瓦,=瓦。=成,=54 又可根据磁场强度定义式(2)求出相应各点的磁场强度。 屈=8-证=40-证=0 存2=疗3=0 成--=-0=0 用,--成=0-= 同样可得 成号号 此例结果很难理解。因为通电螺线管内由传导电流激发磁场,H=!。而永磁体内不存在
【例 15-3】一根沿轴向均匀磁化的细长永磁棒,磁化强度为 ,求图中各点的 和 。 【解】由 可知 M 表示磁棒单位长度上的磁化电流,长直永磁棒相当于一个长直螺 线管。可以直接写出图示各点的磁感应强度: , 又可根据磁场强度定义式(2)求出相应各点的磁场强度。 同样可得 , 此例结果很难理解。因为通电螺线管内由传导电流激发磁场, 。而永磁体内不存在

传导电流,却存在豆,则豆是什么含义呢?这是因为历史原因,当人们认识到电流激发磁 场以前,认为永磁体是磁荷激发的磁场。请看下例。 乡【创15-】一根沿轴向均匀磁化的横截面积为S的细长水磁棒,磁化强度为,试 家围中日对因合路径L的线积分日可,以及7对阿合自面3的适量日的 为多 少? 151 【解】本题中由于没有传导电流,所 以 =0 (1) 而闭合曲面S的及通量 i8-2-购西-话西-0-M=版 (2) 本例计算到此应该结束了,但为了对永磁体问题中的豆物理意义有个了解,对历史上的磁 荷观点作一简单的介绍: 在水磁体问题中,由(1)(2)式表明磁场强度日是个保守场,是个有源场,与静电场相 啦di=0 手=旦 在静电场中有 及 若将(2)式改写成与静电场中的相似形式 ds=9 o (3) 与静电场类比,若称9”为磁荷,将(2)式的闭合曲面S缩小到仅包围磁棒的端面,(2) 式的积分值并不改变,可认为磁荷均匀分布在端面上。现将(2)式与(3)式比较,可得磁 荷面密度:
传导电流,却存在 ,则 是什么含义呢?这是因为历史原因,当人们认识到电流激发磁 场以前,认为永磁体是磁荷激发的磁场。请看下例。 【例 15-4】一根沿轴向均匀磁化的横截面积为 S 的细长永磁棒,磁化强度为 ,试 计算图中 对闭合路径 L 的线积分 ,以及 对闭合曲面 S 的通量 为多 少? 【解】本题中由于没有传导电流,所 以 (1) 而闭合曲面 S 的 通量 (2) 本例计算到此应该结束了,但为了对永磁体问题中的 物理意义有个了解,对历史上的磁 荷观点作一简单的介绍: 在永磁体问题中,由(1)(2)式表明磁场强度 是个保守场,是个有源场,与静电场相 仿。 在静电场中有 及 若将(2)式改写成与静电场中的相似形式 (3) 与静电场类比,若称 为磁荷,将(2)式的闭合曲面 S 缩小到仅包围磁棒的端面,(2) 式的积分值并不改变,可认为磁荷均匀分布在端面上。现将(2)式与(3)式比较,可得磁 荷面密度: