
第八章 分析实验数据处理 8-1数据的特征及分布 一、数理统计的某些基本概念 1、总体与样本 体:被研究对象某特性值的全体。 个 体:组成总体的每个单元。 样本(子样):自总体中随机抽取的一部分个体。 样本容量:样本中所包含个体的数目,用表示。 2、随机变量 来自同一总体的无限多个测量值都是随机出现的, 叫随机变量。 多次重复测定的结果不能相同,也不能事先知道。 测量值一经取定就是一个常量,不再有随机性
8-1 数据的特征及分布 一、数理统计的某些基本概念 1、总体与样本 总 体 : 被研究对象某特性值的全体。 个 体 : 组成总体的每个单元。 样本(子样): 自总体中随机抽取的一部分个体。 样 本 容 量 : 样本中所包含个体的数目,用n表示。 2、随机变量 来自同一总体的无限多个测量值都是随机出现的, 叫随机变量。 多次重复测定的结果不能相同,也不能事先知道。 测量值一经取定就是一个常量,不再有随机性。 第八章 分析实验数据处理

二、随机变量的频数分布 〈例)学生测定BaCl22H0试剂中Ba含量 (%),共有190个数据,区间为55.48% 56.46%。将这些数据按组距0.1来分成10组。 频数:每组中数据的个数 相对频数:频数在总测定 次数中所占的分数 以各组区间为底相对频数 为高做成一排矩形的相对 频数分布直方图 相对频数分布直方图
二、随机变量的频数分布 〈例〉 学生测定 BaCl2·2H2O 试剂中 Ba 含 量 ( % ),共有 190 个数据,区间为 55.48%- 56.46%。将这些数据按组距0.1来分成10组。 频数:每组中数据的个数 相对频数:频数在总测定 次数中所占的分数 以各组区间为底相对频数 为高做成一排矩形的相对 频数分布直方图

其特点: 1,离散特性:测定值在平均值周围波动, 波动的程度用总体标准偏差表示 ∑x- 总体标准偏差 2.集中趋势:向平均值集中 总体平均值 n-oon 在确认消除系统误差的前提下,总体平均值就是真 值
其特点: 1. 离散特性: 测定值在平均值周围波动, 波动的程度用总体标准偏差表示 n x n i ∑ i = − = 1 2 ( µ) σ 2. 集中趋势:向平均值集中 ∑ = →∞ = n i i n x n 1 1 µ lim 总体平均值 总体标准偏差 在确认消除系统误差的前提下,总体平均值就是真 值
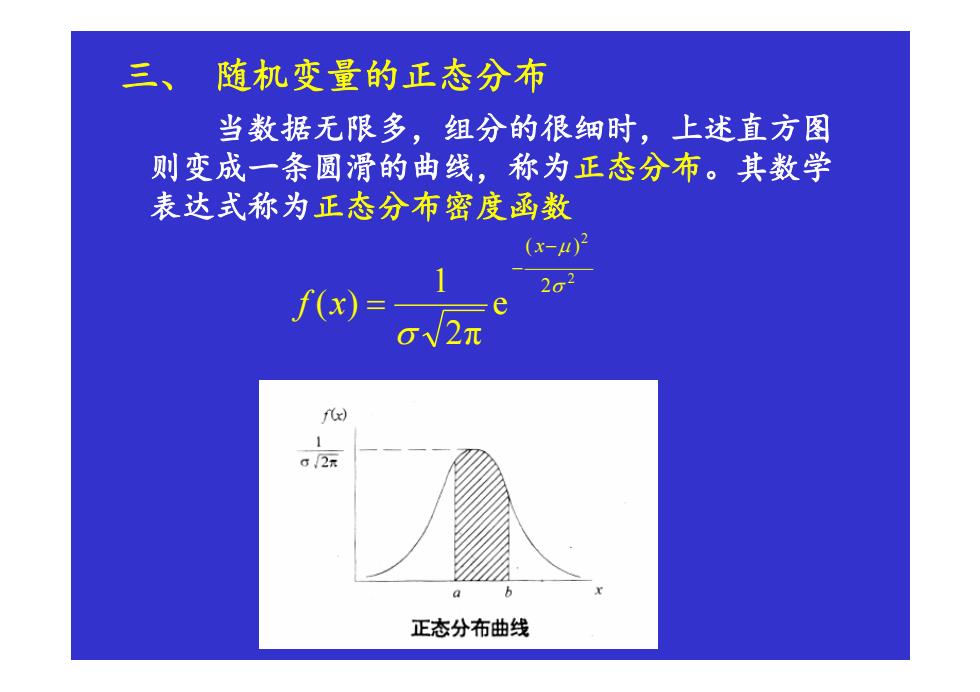
三、随机变量的正态分布 当数据无限多,组分的很细时,上述直方图 则变成一条圆滑的曲线,称为正态分布。其数学 表达式称为正态分布密度函数 (x-u)2 2o3 f(x)= gV2π fx) 1 02元 a 正态分布曲线
三、 随机变量的正态分布 当数据无限多,组分的很细时,上述直方图 则变成一条圆滑的曲线,称为正态分布。其数学 表达式称为正态分布密度函数 2 2 2 ( ) e 2 π 1 ( ) σ µ σ − − = x f x
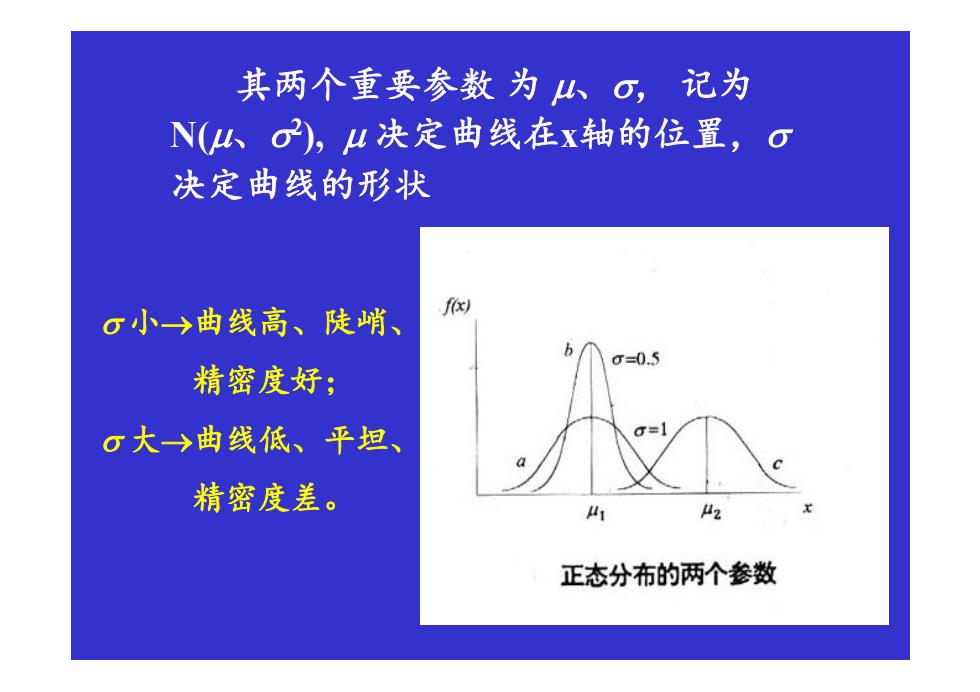
其两个重要参数为山、6,记为 N(山、O2),4决定曲线在x轴的位置,o 决定曲线的形状 σ小→曲线高、陡峭 f划 σ=0.5 精密度好; σ大→曲线低、平坦、 o=l 精密度差。 2 正态分布的两个参数
其两个重要参数 为 µ、 σ, 记为 N(µ、 σ2), µ 决定曲线在 x轴的位置, σ 决定曲线的形状 σ 小 →曲线高、陡峭、 精密度好; σ 大 →曲线低、平坦、 精密度差

随机误差符合正态分布 1.大误差出现的几率小,小误差出现的几率大。 2,绝对值相等的正负误差出现的几率相等。 3,误差为零的测量值出现的几率最大。 所有测量值出现的概率总和应为1,即 (x-4)2 2 e dx =1 -00 求变量在某区间出现的概率,即对该区间求积分 (x-)2 P(a,b)=- 20 dx N2π
随机误差符合正态分布 1.大误差出现的几率小,小误差出现的几率大。 2.绝对值相等的正负误差出现的几率相等。 3.误差为零的测量值出现的几率最大。 所有测量值出现的概率总和应为 1,即 e d 1 2 π 1 ( , ) 2 2 2 ( ) −∞ ∞ = = − ∞ − ∫− ∞ P x x σ µ σ 求变量在某区间出现的概率,即对该区间求积分 P a b x x b a e d 2 π 1 ( , ) 2 2 2 ( ) σ µ σ − − ∫ =
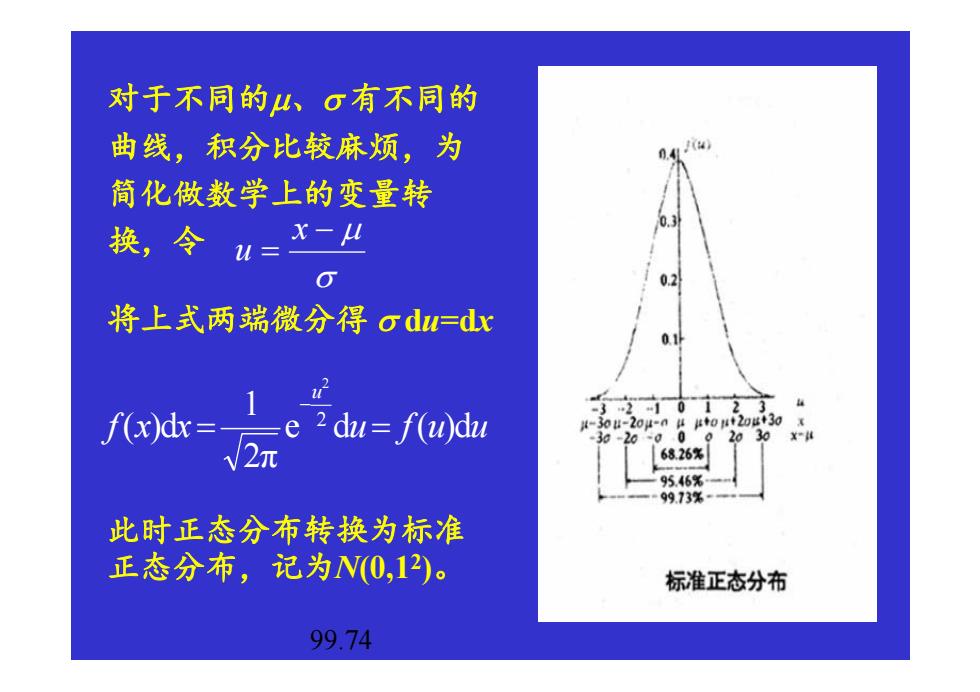
对于不同的山、o有不同的 曲线,积分比较麻烦,为 简化做数学上的变量转 换,令1= X-4 0 将上式两端微分得odu=dx 12 f(x)dx=-e 2du=f(u)du 30-204-n 2π 6826% 95.46% 99.73%- 此时正态分布转换为标准 正态分布,记为N(0,1)。 标准正态分布 99.74
对于不同的µ、σ 有不同的 曲线,积分比较麻烦,为 简化做数学上的变量转 换,令 σ − µ = x u 将上式两端微分得 σ du=dx f x x u f u u u e d ( )d 2π1 ( )d 2 2 = = − 此时正态分布转换为标准 正态分布,记为N(0,12)。 99.74

u 积分P= e2du已被做成概率积分表 √2π0 正态分布概率积分表 面积 wl 面积 | 面积 0.0 0.0000 1.0 0.3413 20 0.4773 0.1 0.0398 1.1 0.3643 21 0.4821 02 0.0793 12 03849 22 0.4861 0.3 0.1179 1.3 04032 2.3 0.4893 4 0.1554 14 Q.192 2.4 0.4918 0.5 01915 1.5 04332 25 0.4938 0.6 0.2258 1.6 Q.4452 26 0.4953 0.7 0.2580 1.7 0.4554 27 0.4965 0.8 02881 1.8 0641 28 0.4974 0.9 0.3159 1.9 0.4713 29 0.4987
积分 已被做成概率积分表 P u u u e d 2 π 1 2 0 2 − ∫ =

u x-u P% M=士1 土0 G u+o P=2×0.3413=0.6826=68.26% u户±2 ±2o u-20 +2G P=2×04773=0.9546=95.46% M=±3 ±3a L-3G +3o P=2×0.4987=0.9974=99.74% 按照正态分布x在区间(-0.5o,+1.5o出现的概率 解:根据 =-4 0 可将h0.5o≤≤H1.5o变换为-0.5≤u≤1.5 查表u=0.5时面积为0.1915 u=1.5时面积为0.4332 则-0.5≤u≤1.5的总面积即为x在区间(4-0.5o, 4+1.5o)出现的概率P=0.1915+0.4332=0.6247
u x -μ x P % u=±1 ±σ µ-σ µ+σ P=2× 0.3413 = 0.6826 =68.26% u=± 2 ± 2σ µ-2σ µ+2σ P=2× 0.4773 = 0.9546 =95.46% u=± 3 ± 3σ µ-3σ µ+3σ P=2× 0.4987 = 0.9974=99.74% 按照正态分布x在区间(µ-0.5σ, µ+1.5σ)出现的概率 解: 根据 σ x u − µ = 可将 µ-0.5σ ≤x ≤µ+1.5σ 变换为 -0.5≤u ≤1.5 查表 u=0.5 时 面积为0.1915 u=1.5 时 面积为0.4332 则-0.5≤ u ≤1.5的总面积即为x在区间( µ - 0.5σ , µ +1.5σ )出现的概率 P = 0.1915 + 0.4332=0.6247
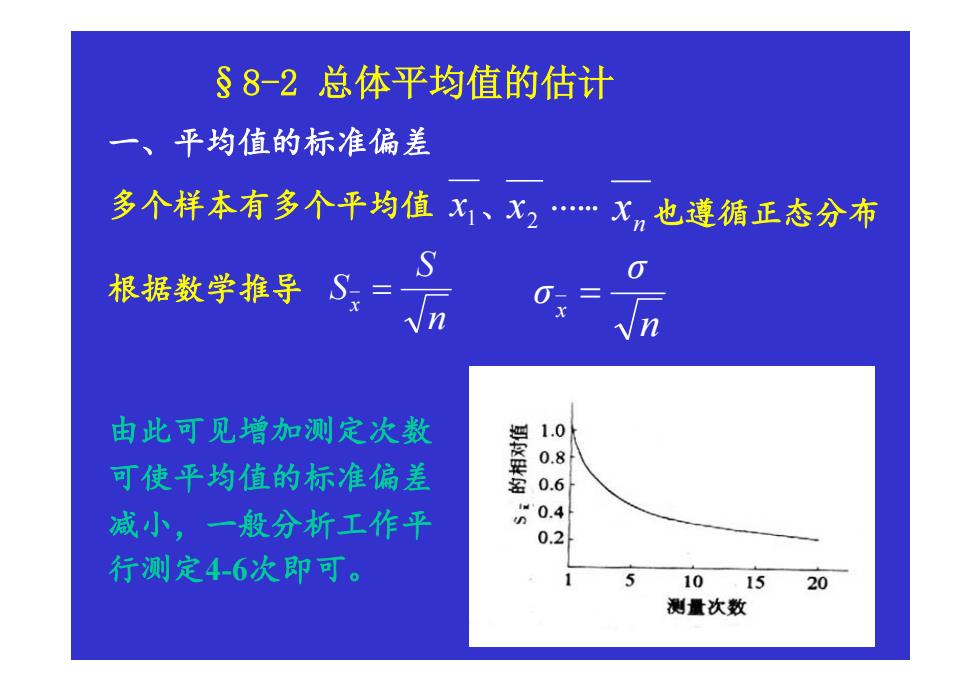
§8-2总体平均值的估计 一、平均值的标准偏差 多个样本有多个平均值x1、X2X,也遵循正态分布 S 根据数学推导S= n 由此可见增加测定次数 1.0 0.8 可使平均值的标准偏差 减小,一般分析工作平 00.4 0.2 行测定4-6次即可。 10 15 20 测量次数
§8-2 总体平均值的估计 一、平均值的标准偏差 多个样本有多个平均值 1 x 2 x n 、 . x 也遵循正态分布 根据数学推导 n S S x = n σ σ x = 由此可见增加测定次数 可使平均值的标准偏差 减小,一般分析工作平 行测定4-6次即可